Radiazione da corpo nero Teoria di Planck

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Radiazione da corpo nero Teoria di Planck

Il Corpo Nero o Radiazione da Corpo Nero
“Teoria di Planck”

di Diego Tasselli (astrofisico)

Il Corpo Nero, è un corpo in perfetto equilibrio termico, in cui l’energia irradiata (o energia prodotta), è uguale all’energia che lo irradia (o energia assorbita).

Esempio di Corpo Nero,
(si può notare che il fotone non riesce a riuscire)

Infatti esso non riflette alcuna radiazione ed appare perfettamente nero.

Nonostante il nome, il corpo nero irradia comunque, e deve il suo nome solo all'assenza di riflessione. Lo spettro (cioè l’intensità della radiazione emessa ad ogni lunghezza d'onda) di un corpo nero è caratteristico, e dipende unicamente dalla sua temperatura.
La luce emessa da un corpo nero è detta radiazione del corpo nero e la densità d’energia irradiata spettro di corpo nero.
La differenza tra lo spettro di un oggetto (stella, nebulosa, ammasso stellare), e quello di un corpo nero ideale, permette di individuare la composizione chimica di tale oggetto.

Il termine "corpo nero" fu introdotto da Gustav Kirchhoff nel 1862. Lo spettro di un corpo nero fu correttamente interpretato per la prima volta da Max Planck, il quale dovette affermare che la radiazione elettromagnetica può propagarsi solo in pacchetti discreti (definiti quanti), la cui l’energia era proporzionale alla frequenza dell'onda elettromagnetica.

L'intensità della radiazione di un corpo nero alla temperatura T è data dalla legge della radiazione di Planck:

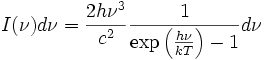
$I(\nu)d\nu = \frac{2h\nu^{3}}{c^2}\frac{1}{\exp\left(\frac{h\nu}{kT}\right)-1}d\nu$

dove I(ν)δν è la quantità di energia per unità di superficie, per unità di tempo e per unità di angolo solido, emessa nell'intervallo di frequenze compreso tra ν e ν+δν; h è la costante di Planck, c è la velocità della luce e k è la costante di Boltzmann.

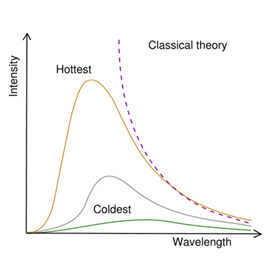
L'andamento delle curve di Planck per il corpo nero. In ascissa la lunghezza d'onda, in ordinata l'intensità.

La lunghezza d'onda alla quale l'intensità della radiazione emessa dal corpo nero è massima, è data dalla legge di Wien ( $\lambda_{max}T=costante= 2898 \mu m \cdot K$ ), e la potenza totale emessa per unità di superficie (appunto, l'intensità) è data dalla legge di Stefan-Boltzmann I = σT4 (con $\sigma=5.67 \cdot 10^{-8} W/m^{2} \cdot K^{4}$ ). Entrambe queste leggi sono deducibili dalla legge dell'irraggiamento di Planck, la prima cercandone il massimo in termini della lunghezza d'onda, la seconda integrando su tutte le frequenze.
Per convenzione, l'oggetto più simile a un corpo nero, è un corpo cavo sul quale è praticato un piccolo foro rispetto alla superficie interna, quest'ultima nera e ruvida (vedi immagine d’inizio articolo). In astronomia, alcuni oggetti come le stelle sono approssimativamente utilizzati come campioni dei corpi neri. Un esempio quasi perfetto di uno spettro da corpo nero, è identificato dalla radiazione cosmica di fondo, la cui temperatura è di circa 2.7 gradi kelvin. È importante ricordare che un qualunque corpo che si trovi a temperatura $T \neq 0$ K è sorgente di radiazione elettromagnetica dovuta al moto di agitazione termica degli atomi che lo compongono. L'emissione di energia elettromagnetica (e.m.) avviene a spese dell'energia termica. Dunque all'interno della cavità sarà sempre presente una radiazione termica e, nel caso in cui la temperatura rimanga costante (condizioni di equilibrio termodinamico), la distribuzione di radiazione è detta spettro di corpo nero.

Passiamo al Calcolo dello spettro di corpo nero

Consideriamo una cavità al cui interno è presente un mezzo con indice di rifrazione η. Inoltre supponiamo che il mezzo sia omogeneo e isotropo per cui η è invariante per rotazioni e traslazioni. Inoltre supponiamo che il dielettrico non sia ferromagnetico per cui $\mu_r \simeq 1$ e $\eta^2 \simeq \epsilon_r$ .

All'interno della cavità è possibile definire una densità di energia elettromagnetica ottenibile a partire dalle equazioni di Maxwell:

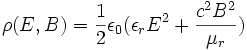
$\rho (E,B)=\frac{1}{2} \epsilon_0 (\epsilon_r E^{2}+ \frac{c^{2}B^{2}}{\mu_{r}})$

per cui l'energia elettromagnetica totale è

W =	∫	ΡdV
	V

A noi interessa calcolare la distribuzione spettrale di energia, ovvero la ρω , dove dρω = ρωdω rappresenta la densità di energia elettromagnetica presente con frequenza compresa tra ω e ω + dω
Attraverso un breve ragionamento è possibile vedere come la ρω possa dipendere esclusivamente dalla frequenza e dalla temperatura, e non dalla forma e dal materiale di cui è costituita la cavità.

Consideriamo infatti due cavità di forma e materiale differente che si trovino alla stessa temperatura T. In entrambe le cavità ci sarà una certa distribuzione di energia elettromagnetica descritta dalle funzioni $\rho_{\omega}^{1}$ e $\rho_{\omega}^{2}$ .
Supponiamo che per una generica frequenza ω valga $\rho_{\omega}^{1}>\rho_{\omega}^{2}$ , allora se uniamo le due cavità attraverso un collegamento ottico con un filtro che permetta il trasferimento di energia alla frequenza ω, noteremo che ci sarà un passaggio di un flusso di energia, dalla cavità 1 alla cavità 2. Questo però va contro il secondo principio della termodinamica perché le due cavità si trovano alla stessa temperatura, dunque concludiamo che dev'essere $\rho_{\omega}^{1}=\rho_{\omega}^{2}$ , e ρω = ρω(ω,T).
Per non complicare troppo il discorso e “la vita o pazienza”, consideriamo una cavità che abbia una geometria semplice, ad esempio un bel parallelepipedo a base quadrata di spigoli 2ω, 2ω.
Supponiamo che le pareti siano perfettamente conduttrici, allora è possibile immagazzinare e conservare energia elettromagnetica all'interno della cavità senza perdite, purché le frequenze corrispondano alle frequenze di risonanza della cavità.
Le frequenze di risonanza della cavità sono quelle per cui si instaurano delle onde stazionarie, quindi nelle tre direzioni devono essere comprese un numero intero di semilunghezze d'onda (vedi vettori gialli all’interno dell’immagine iniziale). Calcolando per un lato:
$l\frac{\lambda}{2}=2a \Longrightarrow \lambda=\frac{4a}{l}$
con l numero intero. Siccome $\omega=2\pi \frac{v}{\lambda}$ si ottiene per la pulsazione $\omega=v \frac{l \pi}{2a}$

Se consideriamo il caso tridimensionalmente, quello che si ottiene è che le frequenze di risonanza della cavità considerata, sono date da:

$\omega= \frac{c}{\eta}\Big[(\frac{l\pi}{2a})^{2}+(\frac{m\pi}{2a})^{2}+(\frac{n\pi}{d})^{2}\Big]^{\frac{1}{2}}$

con l, m, n intesi come numeri interi.

Notando che ω = kv dove k è il famoso vettore d'onda, possiamo riscrivere la precedente come

$\omega= \frac{c}{\eta}\Big[(k_x)^{2}+(k_y)^{2}+(k_z)^{2}\Big]^{\frac{1}{2}}$

Notiamo però che per ogni terna (l, m, n) esistono due modi distinti: il trasversale elettrico e trasversale magnetico.

Per modo si intende una particolare configurazione dei campi elettrico e magnetico che soddisfi la condizione di risonanza.

Il modo trasversale elettrico è tale che: in ogni punto della cavità il campo elettrico è diretto nella direzione perpendicolare a $\hat{z}$ ;
il modo trasversale magnetico è tale che: è il campo magnetico ad avere direzione perpendicolare a $\hat{z}$ per ogni punto.

Vogliamo ora calcolare qual è il numero di modi compresi tra 0 ed una generica frequenza ω, in modo tale da avere un vettore d'onda compreso in modulo tra 0 e $\frac{\omega \eta}{c}$ .

Qui però entra in campo una nuova variabile: lo spazio delle fasi. Infatti tutti i punti individuati da (kx,ky,kz) che rispettano la condizione di risonanza, formano un reticolo la cui cella unitaria ha dimensioni

$(\frac{\pi}{2a}, \frac{\pi}{2a}, \frac{\pi}{d})$ . La condizione $0 \leq k \leq \frac{\omega \eta}{c}$ individua una sfera nello spazio delle fasi.

Ogni celletta ha in progressione contigua 8 modi (i vertici), e allo stesso tempo ogni vertice è condiviso da 8 cellette. Possiamo concludere che abbiamo 1 modo per ogni cella (in realtà due perché per ogni terna (kx,ky,kz) c'è un modo trasversale elettrico e trasversale magnetico come visto prima).

È facile adesso calcolare il numero di modi compresi all'interno della sfera, tenendo conto che siamo interessati ad un solo ottante perché l, m, e n sono numeri naturali e come tali positivi:

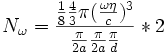
$N_{\omega}=\frac{\frac{1}{8} \frac{4}{3} \pi (\frac{\omega \eta}{c})^{3} }{\frac{\pi}{2a} \frac{\pi}{2a} \frac{\pi}{d}}*2$
cioè $N_{\omega}=\frac{1}{3} \frac{\omega^{3} \eta^{3}}{c^{3} \pi^{2}} V$ dove V è il volume della celletta nello spazio delle fasi.

Per arrivare alla ρω ci interessa valutare il numero di modi per unità di volume e di frequenza, quindi ci interessa

$p_{\omega}=\frac{1}{V} \frac{d N_{\omega}}{d \omega} = \frac{\omega^{2} \eta^{3}}{c^{3} \pi^{2}}$

A questo punto è semplice passare alla densità spettrale di energia.

Infatti è sufficiente moltiplicare la precedente formula, per il valor medio dell'energia dei modi alla frequenza ω. Proprio in questo passaggio la fisica classica si interrompe, (poiché non riesce a spiegare l'andamento della distribuzione spettrale della radiazione emessa da un corpo nero) ed interviene la legge di M Planck.

Definizione di Distribuzione di energia elettromagnetica

Classicamente la distribuzione di energia elettromagnetica presente nella cavità, dovuta al moto di agitazione termica dei vari atomi delle pareti, deve essere la stessa di quella degli oscillatori armonici che si trovano ad una temperatura T. Se prendiamo in considerazione una frequenza ω, la meccanica statistica ci dice che la probabilità che uno di questi oscillatori alla frequenza ω e temperatura T abbia energia compresa tra E ed E + dE è data dalla legge di Boltzmann:

$d P(E)=C e^{-\frac{E}{kT}} d E$

Quindi il valor medio dell'energia vale

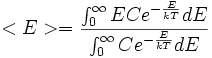
$<E>=\frac{\int_0^{\infty}EC e^{-\frac{E}{kT}} d E}{\int_0^{\infty}C e^{-\frac{E}{kT}} d E}$
Se poniamo $\beta= \frac{1}{kT}$ notiamo facilmente che

$-\frac{d}{d \beta} \ln \int_0^{\infty}e^{-\beta E} d E = \frac{1}{\int_0^{\infty}e^{-\beta E} d E} * \int_0^{\infty}Ee^{-\beta E} d E = <E>$

Quindi abbiamo $<E>=-\frac{d}{d \beta} \ln \Big[-\frac{1}{\beta} e^{-\beta E}\Big]_0^{\infty}= -\frac{d}{d \beta} \ln (\frac{1}{\beta})= \frac{1}{\beta}=kT$

Secondo la fisica classica abbiamo:

$\rho_{\omega}=p_{\omega}<E>=\frac{\omega^{2} \eta^{3}}{c^{3} \pi^{2}}kT$

La precedente è la formula classica di Rayleigh - Jeans e non riproduce affatto i dati sperimentali ricavati precedentemente! Infatti la densità spettrale di energia tende ad infinito per ω tendente ad infinito e quindi per λ tendente a zero. Questo è il così detto fenomeno della catastrofe ultravioletta. Inoltre si vede che integrando la densità spettrale di energia su tutte le frequenze possibili si ottiene una densità di energia infinita!
Ed è proprio qui che entra in gioco Planck. Egli supera i problemi della fisica classica supponendo che la radiazione elettromagnetica sia quantizzata, cioè egli discretizza l'energia dei modi considerandola multipla di una quantità legata alla frequenza del modo stesso:

En = nhν

Allo stesso tempo, egli introduce una nuova valutazione di probabilità:

la probabilità che il modo in questione possegga una energia En vale:

$P(E_n)=Ce^{\frac{-n \hbar \omega}{kT}}$

inoltre, siccome l'energia è discretizzata, gli integrali sono sostituiti da sommatorie e il valor medio dell'energia vale

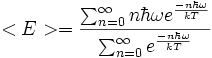$<E>=\frac{\sum_{n=0}^{\infty}n\hbar \omega e^{\frac{-n \hbar \omega}{kT}}}{\sum_{n=0}^{\infty} e^{\frac{-n \hbar \omega}{kT}}}$ anche in questo caso si ha: $<E>=-\frac{d}{d \beta} \ln \big[ \sum_{n=0}^{\infty}e^{-n \hbar \omega \beta}\big]$

La sommatoria che compare nella precedente espressione, è una serie geometrica di ragione $e^{-\hbar \omega \beta}$ per cui:

$<E>=-\frac{d}{d \beta} \ln \big[\frac{1}{1-e^{-\hbar \omega \beta}}\big]=\frac{\hbar \omega}{e^{\hbar \omega \beta}-1}$

e, con i vari passaggi intermedi, finalmente riusciamo ad ottenere l'espressione della densità spettrale di radiazione del corpo nero:

$\rho_{\omega}=\frac{\hbar \eta^{3} \omega^{3}}{\pi^{2} c^{3} [e^{\frac{\hbar \omega}{kT}}-1]}$

La precedente espressione, riproduce bene i dati sperimentali se $h=2\pi \hbar=6.32 \cdot 10^{-34}\, J s$

Inoltre, il numero medio di fotoni per modo è dato da $\bar{q}=\frac{<E>}{h\nu}=\frac{1}{e^{\frac{h\nu}{kT}}-1}$

E, per frequenze nel campo ottico $(\nu \simeq 10^{14}Hz)$ alla temperatura T=300 K, vale

$\bar{q} \simeq e^{-40}\simeq 10^{-18}$ .

Si capisce quindi che a temperatura ambiente l'emissione nella banda del visibile è praticamente trascurabile.

Alcune leggi sono collegate alla Teoria del Corpo Nero.
Abbiamo infatti le leggi di Wien e di Stefan – Boltzmann.

- Legge di Wien

La legge di Wien viene prodotta, andando a considerare per quale lunghezza d'onda si ha un massimo di emissione. Per fare questo bisogna prima trasformare l'espressione della distribuzione spettrale in funzione di λ:
$\rho_{\omega} d \omega = \rho_{\omega} \frac{d \omega}{d \lambda} d \lambda = \rho_{\lambda} d \lambda$
$\omega=2 \pi \frac{c}{\lambda}$
$d \omega = -\frac{2 \pi c}{\lambda^{2}} d \lambda$

per cui $\rho_{\omega} d \omega = \frac{\eta^{3}\frac{(2\pi c)^{3}}{\lambda^{3}}\hbar}{\pi^{2}c^{3}\big[e^{\frac{2 \pi \hbar c}{\lambda k T}}-1\big]}\Big(\frac{-2 \pi c}{\lambda^{2}}\Big)d \lambda$

e infine $\rho_{\lambda} d \lambda = \frac{8 \pi h c \eta^{3}}{\lambda^{5}\big[e^{\frac{hc}{\lambda k T}}-1\big]} d \lambda$

Per semplificare i calcoli poniamo $x=\frac{hc}{\lambda k T}$ e troviamo il massimo della funzione spettrale derivando rispetto a x:

$\frac{d \rho_{\lambda}}{d x}=0 \Longrightarrow e^{-x}+\frac{x}{5}-1=0$

La precedente è un'equazione trascendente la cui soluzione è x = x0 = 4.9651, quindi

$\frac{hc}{\lambda_{max} k T}=x_0=cost$

e infine λmaxT = b

con b costante, abbiamo $b=2.8978 \cdot 10^{-3} mK$

La precedente espressione, esprime la legge di Wien per cui: “all'aumentare della temperatura il massimo di emissione si sposta verso lunghezze d'onda minori e quindi energie maggiori”.

Se ne deduce che al variare della temperatura del corpo varia il colore!

Introduciamo quindi il concetto di temperatura di colore, che esprime la temperatura a cui corrisponde un determinato massimo di emissione. Questo metodo di calcolo, è utilizzato in molti campi oltre che all’astrofisica e ci permette di capire quale sia ad esempio, la temperatura di una stella anziché un’altra, o di capire la temperatura di forni particolarmente potenti, per i quali è chiaramente impossibile pensare all'utilizzo di un termometro.

- Legge di Stefan – Boltzmann

La legge di Stefan - Boltzmann serve a calcolare l'intensità di radiazione emessa, quindi dobbiamo passare a calcolarci l'espressione della densità di energia, integrando la densità energetica spettrale, su tutta la banda di frequenze:

$\rho = \int_0^{\infty}\frac{\hbar \eta^{3} \omega^{3}}{\pi^{2} c^{3} [e^{\frac{\hbar \omega}{kT}}-1]} d \omega$

$x=\frac{\hbar \omega}{kT}$

$\rho = \frac{\eta^{3}(kT)^{4}}{\pi^{2} c^{3} \hbar^{3}} \int_0^{\infty} \frac{x^{3}}{e^{x}-1} d x$

L'integrale che compare nella precedente è noto e vale 6.4938. Quindi abbiamo un valore di $\rho= 7.5643 \Big( \frac{J K^{-4}}{m^{3}}\Big)\eta^{3}T^{4}$

La densità di energia è chiaramente energia emessa per unità di volume. Inoltre l'intensità è data dalla energia per unità di superficie e di tempo, quindi in pratica una densità per una velocità. Ne consegue che:
la dipendenza da T non cambia e si può scrivere F(T) = σT4

Adesso abbiamo ricavato l’espressione che esprime la legge di Stefan - Boltzmann cercata.

F è detta emittanza di radiazione, e σ è la costante di Stefan - Boltzmann che vale

$\sigma= 5.6693 \cdot 10^{-8} \, W m^{-2} K^{-4}$

Si noti che l'intensità di emissione K, va indicata con la quarta potenza della temperatura.

Fonte: http://www.castfvg.it/articoli/fisica/corpo_nero.doc

Sito web da visitare: http://www.castfvg.it

Autore del testo: indicato nel documento di origine

Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.

Radiazione da corpo nero Teoria di Planck

"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco

www.riassuntini.com dove ritrovare l'informazione quando questa serve