Moto periodico

In generale una funzione si dice periodica se:

f(x) = f(x + X)

  Cioè se, trascorso un intervallo X che viene detto periodo della funzione, l’andamento della funzione stessa si ripete in  modo identico.

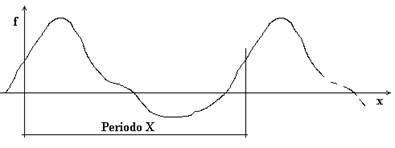
Fig.4.1

  E’ da osservare che in qualunque macchina, grandezze quali momenti e forze (anche di inerzia) hanno certamente andamento periodico in funzione della rotazione J dell’albero perché, dopo una certa rotazione Θ, tutti gli organi si saranno riportati nella posizione di partenza per cominciare un nuovo ciclo.

 

            4.2 MOTO ARMONICO

  Un moto armonico x (t) è rappresentato dalla funzione:

x(t) = X sin(wt+j0)

Dove:
X è l’ampiezza del moto
ω è la pulsazione
j0 è la fase iniziale; risulta: j0 = w t0 è

  La pulsazione (espressa in rad/s) è legata al periodo T (espresso in secondi) ed alla frequenza f (espressa in Herz =1/s):

T = 2p/w  ;    f = 1/T = w/2p  Hz

  Qualunque grandezza armonica può essere rappresentata graficamente come la proiezione di un vettore rotante di modulo pari all’ampiezza, che ruota con una velocità angolare ω. In fig.4.2 è rappresentato il vettore rotante e la funzione armonica.

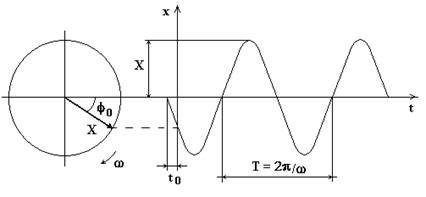
Fig.4.2

  Nella figura il vettore rotante è rappresentato nella posizione che esso occupa nell’istante t=0 e, quindi, risulta sfasato rispetto all’asse orizzontale di un angolo pari alla fase iniziale j0. Il valore della grandezza armonica è dato, istante per istante, dalla proiezione del vettore sull’asse orizzontale.

Velocità
L’espressione della velocità in un moto armonico si ottiene semplicemente derivando l’equazione

x’(t) = wX cos(wt+j0) = wX sin(wt+j0+p/2)

e quindi può essere rappresentato da un vettore rotante di ampiezza ωX, pulsazione ω sfasato di π/2 in  anticipo rispetto al vettore X; la proiezione del vettore ωX sull’asse orizzontale e quindi il valore istantaneo della velocità.

            Accelerazione
Derivando la precedente relazione si ottiene la accelerazione:

x”(t) = -w2X sin(wt+j0) = w2X sin(wt+j0+p)

  Il valore istantaneo dell’accelerazione è dunque la proiezione di un vettore rotante di ampiezza ω2 X sfasato di π (in opposizione di fase) rispetto al vettore X.
In fig.4.3 sono rappresentati i vettori rotante che rappresentano spostamento, velocità ed accelerazione.

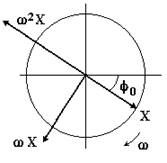
Fig.4.3

 

            4.3 Composizione di moti armonici

  Si considera ora il moto che risulta dalla composizione di due moti armonici diretti, in un primo caso, secondo lo stesso asse ed in un secondo caso secondo assi ortogonali.

4.3.1 Composizione di moti armonici diretti secondo lo stesso asse

  Si considerino due moti armonici:

x1(t) = X1 cos(w1t+j0,1)
x2(t) = X2 cos(w2t+j0,2)

  Come si è visto nel paragrafo precedente una grandezza armonica può essere vista come la proiezione su di un asse di un vettore rotante; in fig.4.4 sono rappresentati i due vettori x1 e x2, la cui proiezione sull’asse orizzontale rappresenta il valore istantaneo delle funzioni x1 (t) ed x2 (t).


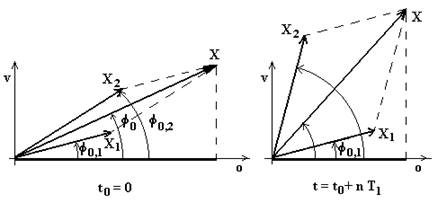
Fig.4.4

  Per quanto detto il moto risultante dei due moti armonici, è pari a:

x(t) = X1 cos(w1t+j0,1) + X2 cos(w2t+j0,2)

e coincide con la proiezione sull’asse orizzontale, del vettore X risultante di x1 ed x2.
Si possono distinguere tre casi:

            1) I due moti armonici hanno la stessa pulsazione.
In questo caso, essendo ω1 = ω2 = ω, il moto risultante sarà:

x(t) = X cos(wt+j0)

cioè un moto armonico di pulsazione ω, ampiezza pari a:

e fase iniziale data da:

  Dalla fig.4.4, si comprende che, avendo i due vettori rotanti la stessa velocità, la loro posizione relativa non cambia e quindi il loro risultante è un vettore rotante con velocità ω ed intensità costante.

2) I due moti armonici hanno pulsazione diversa.
Se il rapporto tra le due pulsazioni è un numero razionale esisterà un tempo T, tale che:

T = K1T1 = K2T2

Ossia, trascorso un tempo t = t0 + T, i due vettori rotanti x1 e x2 assumeranno le stesse posizioni occupate nell’istante t0 ed il moto risultante si ripeterà identicamente e pertanto esso sarà periodico di periodo T.
Se invece il rapporto tra le due pulsazioni non è un numero razionale, non si potrà mai verificare che in un istante t siano trascorsi contemporaneamente un numero intero di periodi di x1(t) ed un numero intero di periodi di x2 (t). Per questo motivo il moto risultante sarà aperiodico.

3) I due moti armonici hanno pulsazioni prossime tra di loro.
In questo caso il moto risultante sarà ancora un moto aperiodico essendo il rapporto tra le due pulsazioni (molto prossime tra di loro) generalmente un numero non razionale.
E’ da osservare, però, che, essendo:

se si fa riferimento alla rappresentazione grafica dei moti armonici, si comprende facilmente che la posizione relativa tra i due vettori rotanti cambia lentamente essendo le due velocità di rotazione prossime tra loro. Se si considera un particolare istante t* nel quale i due vettori sono in fase (sovrapposti l’uno all’altro), in tale istante sarà x =  x1 + x2 ; a causa della diversa velocità di rotazione dei due vettori, dopo un certo tempo essi saranno in opposizione di fase ed il loro risultante assumerà il minimo valore possibile: x =  x1 - x2. Trascorso un ulteriore tempo, uguale al precedente, i due vettori saranno di nuovo in fase ed il loro risultante assumerà, di nuovo, il massimo valore possibile. Tale risultante, però, non avrà la stessa direzione che aveva nell’istante t* se il rapporto ω1 / ω2 non è un numero razionale.
Da quanto detto si evince che il risultante di x1 ed x2 passa da un massimo ad un massimo successivo ad intervalli costanti di tempo; questi ultimi sono dati da:

  Il moto risultante è del tipo rappresentato in fig.4.5 e prende il nome di battimento. Il tempo Tb è detto periodo del battimento.

 

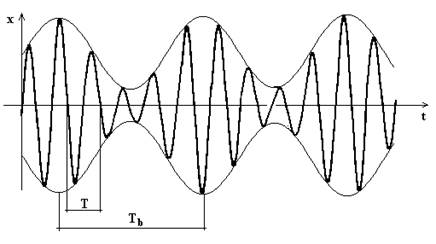
Fig.4.5

            4.3.2 Composizione di moti armonici diretti secondo
assi ortogonali.

  Si prende in considerazione soltanto il caso nel quale i due moti hanno la stessa pulsazione ω.
Siano x ed y due assi ortogonali tra di loro, i due moti armonici saranno:

x(t) = X cos(wt+j0,x)
y(t) = Y cos(wt+j0,y)

  Il moto risultante dipende dalla differenza di fase Δj = j0,x - j0,y  tra i due moti

• Se Δj = π/2, l’espressione analitica dei due moti è:

x(t) = X cos(wt+j0)
y(t) = Y cos(wt+j0+p/2) = Y sin(wt+j0)
Quadrando e sommando le due relazioni si ottiene l’equazione di un ellisse avente semiassi pari ad X ed Y coincidenti con i due assi x ed y: (V. fig.4.6,a)

                        x2/X2 + y2/Y2 = 1

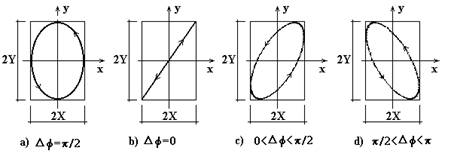
Fig.4.6

• Se Δj = 0 l’espressione analitica dei due moti diventa quella di una retta:

 

y = Y/X x

che risulta essere la diagonale di un rettangolo di lati 2x e 2y (V. fig.4.6,b).

• Se è 0< Δj < π/2, il moto risultante sarà ancora un ellisse inscritta in un rettangolo di lati 2x e 2y, ma i semiassi di tali ellisse non coincideranno con gli assi x ed y.
• Se infine risulta: π/2 < j < π, il risultante sarà ancora un ellisse come nel caso c), ma con i semiassi inclinati da parte opposta al caso precedente.

  In conclusione, la somma di due moti armonici diretti lungo assi ortogonali ed aventi la stessa pulsazione è una traiettoria inscritta in un rettangolo i cui lati sono pari l’uno a 2X e l’altro a 2Y.
Per Δφ > π le traiettorie sono analoghe ma vengono percorse in verso opposto a quello visto in precedenza.
Le traiettorie di cui sopra prendono il nome di curve di Lissajous dal nome del matematico francese che le ha studiate per primo.

 

4.4 Analisi armonica

  Il matematico francese Fourier dimostrò che una funzione periodica e continua che soddisfi le condizioni di Dirichelet (sempre soddisfate da funzioni che descrivano l’andamento di un fenomeno fisico) può essere scomposta in una serie (dal suo nome detta serie di Fourier) costituita dal valor medio della funzione più una somma di infiniti termini armonici le cui pulsazioni sono multipli interi di una pulsazione detta fondamentale e si susseguono secondo la serie di numeri naturali:

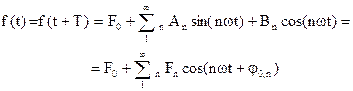
Dove:
F0 = valore medio della funzione
n = 1; 2; 3; … = ordine dell’armonica
Fn = ampiezza dell’armonica di ordine n
ω = pulsazione dell’armonica fondamentale
nω = pulsazione dell’armonica di ordine n
φn = fase dell’armonica di ordine n

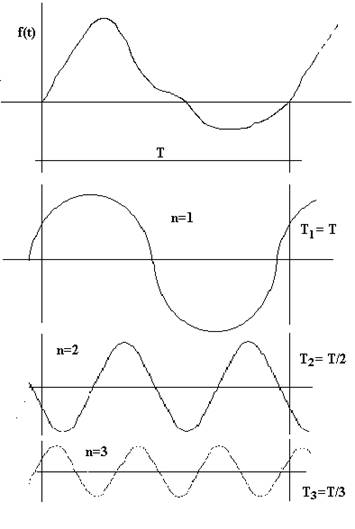
Fig.4.7

  E’ da osservare che i due modi di esprimere la serie di Fourier sono analoghi poiché risulta, come è noto:

-

  Il periodo dell’armonica fondamentale (n = 1) della serie è identico al periodo della funzione periodica; pertanto il periodo della generica armonica di ordine n sarà Tn = T/n.
Effettuare l’analisi armonica di una funzione consiste nel determinare le ampiezze An e Bn, ovvero le ampiezze Fn e le fasi φn delle componenti armoniche.
E’ ancora da osservare che, nelle funzioni che esprimono l’andamento di un fenomeno o di una grandezza fisica, l’ampiezza delle armoniche di ordine elevato sono piccole rispetto a quelle di ordine più basso e tendono a diminuire con l’aumentare dell’ordine dell’armonica. Per questo motivo il contributo di armoniche ad elevata pulsazione può essere trascurato:

  L’analisi armonica ha una notevole importanza perché consente di:
- Riconoscere che una funzione periodica di periodo noto T può esser scomposta in una somma di componenti armoniche le cui pulsazioni sono multipli interi di quella ω = 2π/T della fondamentale.
- Attraverso il calcolo di ampiezze e fasi di un numero finito di termini armonici, ottenere un’espressione analitica che rappresenta con buona approssimazione l’andamento di un fenomeno periodico del quale sono noti un’insieme di dati discreti.

 

4.5 Modelli matematici

  Lo studio di un qualunque fenomeno fisico (meccanico, elettrico, idraulico ecc.) viene affrontato mediante la definizione di un modello matematico.
Definire un modello matematico significa descrivere un sistema fisico con una serie di ipotesi semplificative e scrivere le equazioni di equilibrio per il sistema; nei casi che prenderemo in esame tali equazioni saranno scritte utilizzando il principio di d’Alembert.
Come esempio, consideriamo un sistema costituito da un asta flessibile incastrata ad un’estremità, sulla quale è montato un solido di massa m all’altra estremità (V. fig.4.8,a)

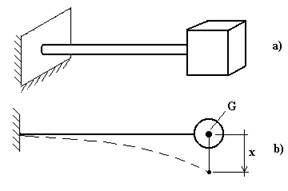
Fig.4.8

  La prima assunzione semplificativa consiste nella discretizzazione del sistema: si suppone che l’asta sia un vincolo elastico privo di massa e che tutta la massa del sistema sia concentrata nel baricentro G del solido all’estremità dell’asta. In questo modo il sistema fisico viene sostituito da un sistema semplificato a parametri concentrati: tutta la massa del sistema è concentrata nel punto G, la deformazione del sistema è quella dell’asta che è dunque considerata come un semplice vincolo elastico privo di massa. Con tali ipotesi semplificative il sistema ha un solo grado di libertà: lo spostamento x, dalla posizione di equilibrio, del punto G. (V. fig.4.8,b).
Applicando il principio di d’Alembert, si scrive l’equazione di equilibrio dinamico del sistema discreto:

  Nella equazione il termine  rappresenta la forza di inerzia mentre il termine  rappresenta la forza di richiamo elastico dovuta alla deformazione dell’asta. Il coefficiente K è detto rigidità del sistema.
Il modello matematico appena descritto non tiene conto di alcuna resistenza passiva. Un modello più accurato può essere ottenuto introducendo una resistenza proporzionale alla velocità del sistema:

La forza  è una resistenza proporzionale alla velocità e, per questo motivo, viene detta resistenza viscosa. L’equazione del moto appena descritto è relativa quindi ad un modello matematico che descrive la realtà fisica in modo più accurato. Il coefficiente   è detto coefficiente di smorzamento viscoso.
Come è facile intuire, le resistenze passive che si oppongono al moto, nella realtà fisica, non sono solo di tipo viscoso, cioè non sono solo forze proporzionali alla velocità. Un modello matematico più accurato terrà conto anche di resistenze proporzionali, ad esempio, al quadrato della velocità. L’equazione del moto che così si ottiene non sarà, però, più un’equazione differenziale lineare e, per tanto, non sarà più integrabile analiticamente.

4.6 Rigidità degli elementi elastici

  Avendo indicato, nelle equazioni del moto, la forza di richiamo elastica con F = Kx, ne segue che la rigidità K è il rapporto fra la forza e la deformazione del sistema:

  Il calcolo della rigidità di un sistema è tanto più difficile quanto maggiore esso è complesso dal punto di vista geometrico; tuttavia è semplice calcolare la rigidità di alcuni elementi “tipo”.

4.6.1 Trave incastrata ad un’estremità (V. fig.4.9,1)

  Per una struttura di questo tipo la scienza delle costruzioni ci fornisce la relazione che lega la freccia f (deformazione della struttura) alla forza F che l’ha provocata:

dove:

E è detto modulo di elasticità normale e rappresenta il rapporto tra la sollecitazione (Forza per unità di superficie della sezione retta) e l’allungamento. In termini più semplici è quella forza per unità di superficie della sezione retta dell’elemento che provocherebbe un allungamento dello stesso del 100%. Esso dipende solo dal materiale e, per l’acciaio vale all’incirca 2,06 x 1011 N/m2.

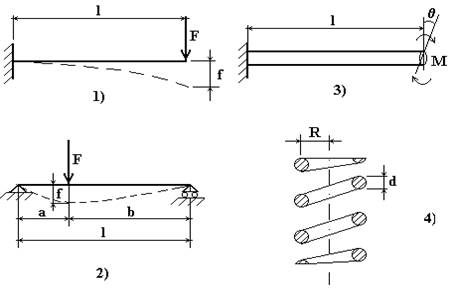
Fig.4.9

  I è il momento di inerzia della sezione retta è dato dal prodotto del raggio di inerzia al quadrato della sezione retta per l’area di quest’ultima. Le sue dimensioni sono, per quanto detto, una lunghezza alla quarta.
La quantità I dipende, quindi, dalla forma e dalle dimensioni della sezione della struttura.
La rigidità del sistema rappresentato schematicamente in fig.4.9,1 è per tanto:

Esempio 4.I:

  Si desidera calcolare la rigidità del sistema rappresentato in fig.4.10,a.

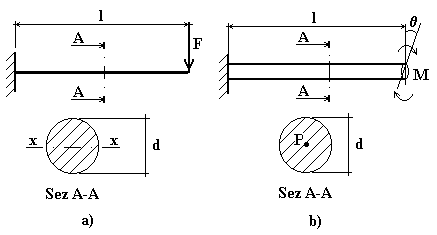
Fig.4.10

  Dati:
l = 200mm
d = 10mm
materiale = acciaio

  Il raggio di inerzia al quadrato rispetto all’asse neutro a torsione xx per la sezione circolare vale:

per cui:

491 mm4 = 4,91x10-10 m4

quindi:
K = (3·2,06x1011·4,91x10-10)/0,23 = 3,79x104 N/m

4.6.2 Trave appoggiata alle estremità (V. fig.4.9,2)

Un elemento elastico schematizzabile con una trave appoggiata alle estremità sulla quale agisce una forza F a distanza a da un appoggio e b dall’altro, in corrispondenza della sezione nella quale è applicata la forza si infetterà di una quantità f data da:

di conseguenza la rigidità in corrispondenza di tale sezione vale:

4.6.3 Trave incastrata ad un’estremità, sollecitata
da un   momento torcente (V. fig.4.9,b)

  Tale elemento elastico è chiamato “barra di torsione”; la sua rigidità è data da:

dove:
 è il modulo di elasticità tangenziale (o trasversale) e, per l’acciaio, vale
IP è il momento di inerzia della sezione retta polare.
Questa rigidità è detta rigidità torsionale ed ha le dimensioni di un  momento torcente diviso un angolo, ossia di una forza per una lunghezza.

            Esempio 4.II:
Per la barra di torsione rappresentata in fig.4.10,b si desidera calcolare la rigidità torsionale.
Dati:
 = 600mm
d = 12mm
materiale: acciaio
Il raggio di inerzia polare per la sezione circolare vale:

per cui:

= p/32 (12x10-3)4 = 2,04x10-9 m4

            La rigidità vale quindi:

K = (8x1010·2,04x10-9)/0,6 = 2,72x102 Nm/rad

4.6.4 Molla ad elica cilindrica  (v. fig.4.9,a)

  In una molla ad elica cilindrica, la rigidità dipende dai seguenti parametri:
R =  raggio medio di avvolgimento
n = numero di spire che si deformano
d = diametro del tondino con il quale è stata costruita.
La sua rigidità vale:

            4.6.5 Rigidità di più elementi elastici

Due o più elementi elastici possono essere collegati tra di loro in serie o in parallelo.

            Rigidità in serie (V. fig.4.11) se sono collegati in modo tale che per il sistema costituito dagli elementi elastici la deformazione complessiva sia la somma delle deformazione di ogni singolo elemento.
In questo caso gli elementi elastici sono sottoposti alla stessa forza F.

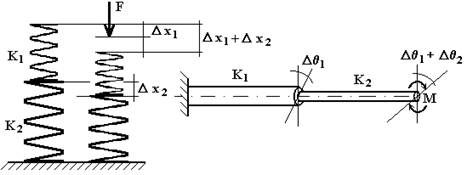
Fig.4.11

  La deformazione del sistema è data da:

                        Dx = Dx1 + Dx2 = F/K1 + F/K2

  Di conseguenza, la relazione che fornisce la rigidità complessiva è:

Dx/F = 1/K = 1/K1 + 1/K2

            Rigidità in parallelo (V. fig.4.12). In questo caso tutti gli elementi elastici subiscono la stessa deformazione; la forza di reazione elastica con la quale reagisce il sistema è data dalla somma delle reazioni dei singoli elementi.

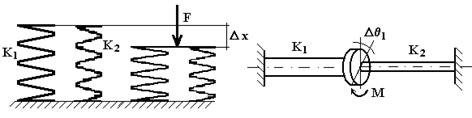
Fig.4.12

  La reazione complessiva del sistema è quindi data da:

F = K1Dx1 + K2Dx2

e, pertanto, la rigidità complessiva è pari a:

 

            4.7 Vibrazioni di sistemi ad 1 grado di libertà

4.7.1 Modelli senza dissipazione di energia

Si considerano, per primi, i modelli matematici nei quali non si tiene conto di resistenze passive.

4.7.1.1 Vibrazioni libere

  Uno schema di un modello di sistema ad 1 grado di libertà è mostrato in fig.4.13. Esso è costituito da una massa m che scorre in guide che sono supposte essere prive di attrito.

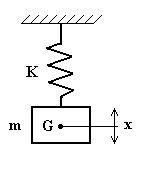
Fig.4.13

  La massa è rigida ed è collegata ad un elemento elastico di rigidità K, a sua volta vincolato ad un punto fisso. La coordinata lagrangiana x del sistema è definita come lo spostamento del baricentro G della massa (o di qualunque altro punto della stessa, avendola considerata rigida) valutato a partire dalla posizione che esso occupa quando il sistema è in quiete.
Applicando il principio di d’Alembert, si scrive l’equazione del moto del sistema:

  La precedente è un’equazione differenziale del secondo ordine, a coefficienti costanti, non completa, omogenea. L’integrale generale è:

che, sostituito nell’equazione del moto, porta a scrivere l’equazione algebrica caratteristica:

da cui:

Si pone:

per cui:

e quindi la legge del moto è data da:

  Tenendo conto delle formule di Eulero, la precedente equazione si può scrivere:

x(t) = A cos wnt + B sin wnt = C cos (wnt +j0)

dove:

 ;          tg j0 = B/A

  Da quest’ultima equazione si vede che il moto libero del sistema schematizzato dal nostro modello, è un moto armonico di ampiezza C e pulsazione ωn; quest’ultima è detta pulsazione naturale del sistema.
L’ampiezza del moto dipende dalle condizioni iniziali del sistema. Posto:

  Sostituendo tali condizioni iniziali nella legge del moto si ottiene:

    Per cui:

x(t) = x0 cos wnt + (x0/wn) sin wnt

ovvero:

x(t) = C cos (wnt +j0)

con: 

 ;         

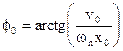
  La legge del moto che si è ricavata mostra che l’ampiezza del moto libero (di pulsazione wn) rimane costante nel tempo, ossia il moto, una volta destato, non si estingue mai. Questo risultato è in contrasto con le osservazioni sperimentali e dipende dal fatto che, nel nostro semplice modello matematico non si è tenuto conto di alcune cause di dissipazioni della energia.
E’ da osservare ancora che nell’equazione del moto non si è tenuto conto della forza peso. L’effetto di quest’ultima è solo quello di spostare, di una quantità costante xP, la posizione di equilibrio statico del sistema e, pertanto non ha nessuna influenza sul suo comportamento dinamico:

  da cui:

  essendo:  Kxp = P

            4.7.1.2 Vibrazioni forzate armoniche

  Si consideri ora che sul sistema rappresentato in fig.4.13 agisca una forza armonica F(t) = F0 cosωt  applicata alla massa come mostrato in fig.4.14.

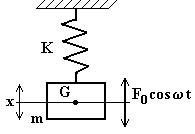
Fig.4.14

 L’equazione del moto è:

ossia:

  L’integrale generale è dato da:

x(t) = C1 cos wnt + C2 sin wnt + Xf  cos wt

  Il primo ed il secondo termine a secondo membro rappresentano il moto libero del sistema e le costanti C1 e C2 vanno determinate sostituendo tale integrale particolare e rappresenta il moto forzato a regime.
Malgrado nel modello non si tenga conto di alcune cause di dissipazione dell’energia, dall’esperienza è noto che, dopo un transitorio iniziale, l’oscillazione libera del sistema (che nel nostro caso viene destata sia dalle condizioni iniziali che dalla applicazione della forza F0 cosωt) si estingue. Per questo motivo, se interessa conoscere la legge del moto a regime, (cioè dopo che il transitorio iniziale si è estinto) si può porre:

x(t) = Xf cos wt

  Sostituendo questo integrale particolare si ha:

-mw2 Xf cos wt + K Xf cos wt = F0 cos wt

da cui:

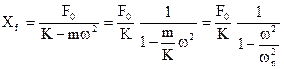
ponendo:

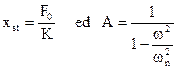
risulta:

Xf = xst A

e quindi:

x(t) = xst A cos wt

  La quantità xst è detta spostamento statico e rappresenta lo spostamento che la massa subisce per la applicazione di una forza costante di intensità F0, applicata staticamente.
Il termine A è detto coefficiente di amplificazione e rappresenta l’amplificazione dell’ampiezza del moto (rispetto allo spostamento statico) per effetto del fatto che la forza è applicata dinamicamente.
L’andamento di A è rappresentato in fig.4.15,a ed in valore assoluto in fig.4.15,b, in funzione di ω/ωn.

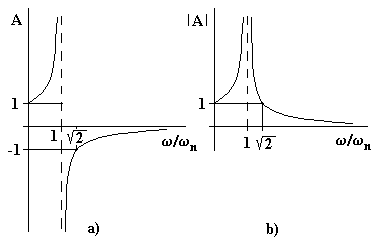
Fig.4.15

  Dall’espressione di A e dai diagrammi di fig.4.15 si evince quanto segue:
- Per valori molto piccoli di ω/ωn, l’amplificazione dinamica è prossima ad uno.
- Per ω/ωn che tende ad 1 il coefficiente di amplificazione tende ad infinito; cioè se la pulsazione della causa forzante è prossima alla pulsazione naturale del sistema, l’ampiezza dell’oscillazione tende ad infinito.
- Per ω/ωn>1, A ha segno negativo assume il valore -1 per ω/ωn=√2 e tende a 0 per ω/ωn tendente all’infinito.
La condizione per la quale ω=ωn è detta risonanza. In corrispondenza della risonanza, risulta A = ∞ perché nel nostro semplice modello matematico non si è tenuto conto di alcuna dissipazione di energia. Nella realtà fisica, in prossimità della risonanza l’ampiezza delle deformazioni del sistema sono tali da portare a rottura.

Vibrazioni forzate dal moto del vincolo.

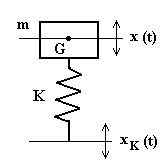
Fig.4.16

  Consideriamo una massa m collegata da un organo elastico di rigidità K ad un punto che si muove con legge armonica:

xK (t) = XK cos wt

  L’equazione del moto è:

ossia:

cioè:

  La quantità KXK ha le dimensioni di una forza e quindi l’equazione appena scritta coincide con quella del moto forzata se si pone KXK = F0.
La legge del moto della massa m è ancora:

x(t) = xst A cos wt

dove:  xst = K XK / K = XK .

            Vibrazioni forzate periodiche
Se la forzante ha andamento periodico, come si è visto nel paragrafo per l’analisi armonica, essa può essere considerata come somma di termini armonici le cui pulsazioni si susseguono come la successione dei numeri naturali. Se il sistema è lineare, vale il principio di sovrapposizione degli effetti: mediante i risultati dei paragrafi precedenti si può calcolare la legge del moto per ciascuna delle componenti armoniche della forzante; il moto del sistema sarà dato dalla somma delle leggi del moto dovuto a ciascuna delle componenti armoniche.
Se è noto il periodo della forzante, è facile calcolare le pulsazioni delle componenti armoniche e quindi valutare se qualcuna di esse è prossima alla pulsazione naturale del sistema.

            4.7.1.3 Esempi di sistemi conservativi ad 1 grado di libertà

  Si esaminano, quindi seguito, alcuni sistemi ad 1 grado di libertà per i quali, quindi, l’equazioni del moto e le leggi del moto sono dello stesso tipo di quelle scritte nei paragrafi precedenti.

            Pendolo semplice
Se si assume come coordinata lagrangiana la posizione angolare J (valutata rispetto alla verticale) l’equazione del moto è:

Dove:
I0 = momento di inerzia di massa del sistema rispetto all’asse di oscillazione (di traccia 0 nella figura) = ml2
KJ= momento di richiamo = P l sinJ = m g l sinJ.
Tale espressione mostra che il momento di richiamo non è lineare; tuttavia, per piccole oscillazioni, si può assumere:  e quindi  .

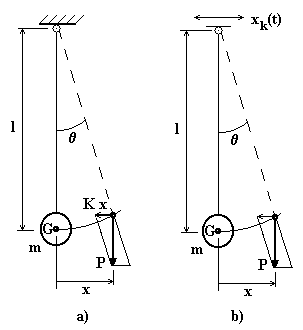
Fig.4.17

  L’equazione del moto si può quindi scrivere:

                       

da cui:

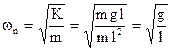
  Come coordinata lagrangiana può essere considerato lo spostamento lineare x dalla posizione di queste. L’equazione del moto, in questo caso, è:

dove:

per piccoli spostamenti:

                       

 e quindi:

da cui:

 

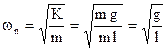
            Moto forzato di un pendolo semplice

  Si consideri il pendolo semplice dell’esempio precedente per il quale il punto di sospensione O si muove (v. fig.4.17,b) con una legge del moto data da:

xK = XK cosωt

  Applicando le relazioni riportate nel par. 4.7.1.2 si può scrivere immediatamente la legge del moto:

 

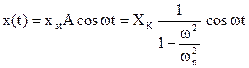
            Moto libero di un pendolo composto

  In fig.4.18 sono rappresentate due viste di un pendolo composto.
L’equazione del moto si scrive :

per cui:

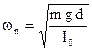
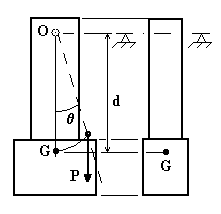
Fig.4.18

  Ricordando che I0 = IG + md2 = m + md2, risulta:

                       

 

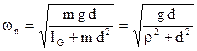
            Applicazione del pendolo composto

Le relazioni scritte per un pendolo composto possono essere impiegate per la determinazione sperimentale del momento di inerzia di massa di un oggetto. Si consideri un volano rappresentato in pianta ed in sezione nella fig.4.19
Si sospende il volano mediante due supporti a coltello, indicati con s, in modo da fare oscillare il volano stesso rispetto ad un asse fisso. Si allontana il pendolo composto così ottenuto dalla posizione di equilibrio mettendolo così in oscillazione e si misura il periodo di oscillazione.
Quest’ultimo sarà dato da:

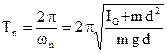
  Nota la massa m e la distanza d dell’asse di oscillazione dall’asse rispetto al quale si vuol conoscere il momento di inerzia di massa IG, quest’ultimo è l’unica incognita nell’equazione appena scritta e può essere ricavato immediatamente.

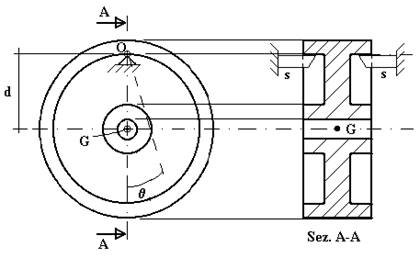
Fig.4.19

            Per effettuare la prova sperimentale con un accettabile precisione occorre tenere presente quanto segue:
- Per misurare il periodo di oscillazione è opportuno prendere il tempo necessario a che un buon numero di oscillazioni siano compiute (tipicamente 2050). E’ difficile infatti valutare correttamente l’inizio e la fine di un oscillazione; questo errore viene compiuto quando si fa partire il cronometro e quando lo si ferma e rappresenta un tempo. Se il tempo misurato è sufficientemente lungo (perché si è contato un buon numero di oscillazioni) l’errore commesso alla partenza ed all’arresto è percentualmente molto modesto.
- E’ opportuno che la quantità di md2 ed IG siano dello stesso ordine di grandezza per ridurre l’influenza degli errori che inevitabilmente si commettono nelle misure delle varie grandezze. Ciò significa che d e  debbano essere dello stesso ordine di grandezza.

Manometro a liquido
Per il manometro rappresentato in fig.4.20, determinare la pulsazione naturale del liquido monometrico. Sono noti:
L = lunghezza rettificata della colonna liquida
Ω = sezione del tubo
δ = densità del liquido

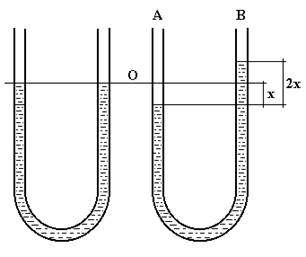
Fig.4.20

  Il sistema ha un grado di libertà rappresentato dallo spostamento x del liquido dalla posizione di equilibrio. Per tale motivo l’equazione del moto del sistema è:

dove:
m = massa della colonna liquida = l Ω δ
Kx = forze di richiamo = 2x Ω δ g
per cui:

  Dunque la pulsazione naturale del sistema dipende solo da l.

  Il manometro dell’esempio precedente è collegato ad un tubo (v. fig.4.21) nel quale la pressione varia con legge armonica con valore medio diverso da zero: p(t) = p0 + p1 cosωt

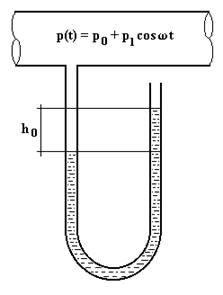
Fig.4.21

  Si desidera leggere il valore medio della pressione (lettura h0) con oscillazioni trascurabili della lettura stessa.
Sono noti:
p0/p1 = rapporto fra il valore medio della pressione e l’ampiezza della parte variabile con legge armonica; p0/p1 = 2
ωn = pulsazione della pressione = rad/s

  Quello descritto è un sistema ad 1 g.d.l. (grado di libertà) sotto l’azione di una forzante armonica.
La lettura dovuta al valore medio della pressione si ottiene dalla relazione di equilibrio tra la forza dovuta alla pressione ed il peso della colonna di fluido alta h0:

p0 W = h0 d g W

da cui:

                        h0 = p0 / (d g)

  Il moto forzato ha ampiezza:

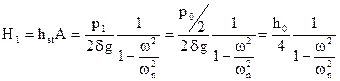
  Se si realizza il manometro in modo che la lunghezza della colonna liquida sia tale che risulti ωn = ω/5, l’ampiezza dell’oscillazione dovute alla parte variabile della pressione varrà:

  Se quindi si fa in modo che risulti ω/ωn = 5, ne consegue che l’ampiezza del moto forzato, cioè l’ampiezza della lettura dovuta alla parte variabile della pressione, è circa 1/100 della lettura dovuta al valore medio della pressione. La lettura quindi fornirà, praticamente, solo il valore di quest’ultima.

 

            Oscillazione torsionali forzate

  Sul sistema torsionale rappresentato schematicamente in fig.4.22 agisce un momento armonico M(t) = M0 cosωt. Calcolare l’ampiezza del moto forzato.

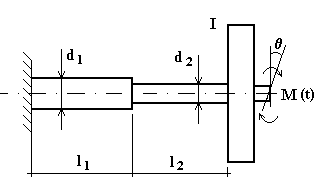
Fig.4.22

  Sono noti:
I = momento di inerzia di massa del disco = 1 kg m2
l1 = 500mm
l2 = 500mm
d1 = 40mm
d2 = 30mm
materiale: acciaio
G = 8,5 x 1010 Nm-2
M0 = 100 Nm
ω = 10 rad/s

  Applicando le relazioni miste per i sistemi forzati ad 1 g.d.l. si scrive immediatamente l’equazione del moto:

e la legge del moto:

l’ampiezza del moto forzato vale:

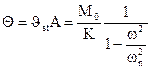
  Occorre quindi calcolare la rigidità del sistema; essa è data dalle rigidità dei due tronchi disposti in serie:

1/K= 1/K1 + 1/K2 

con:

IP1 = p/32 d4 = p/32 (40×10-3) 4 = 2,51×10-7 m4

K1 = G IP1/l = 8,5×1011 2,51×10-7 = 2,14×104 Nm/rad

Analogamente si calcola K2 = 6,76 x 103 Nm/rad
In definitiva:

K = 5,14×103 Nm/rad

E quindi:

In definitiva, l’ampiezza del moto forzato vale:

                       

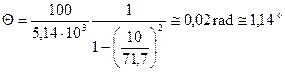
4.7.2 Modelli con attrito viscoso

  Con i modelli nei quali non si tiene conto di alcuna dissipazione di energia si sono ottenuti risultati che descrivono la realtà in modo non del tutto soddisfacente. Per aumentare l’approssimazione si può tenere conto delle cause di dissipazione della energia introducendo, nel modello, una forza proporzionale alla prima potenza della velocità, detta forza di attrito viscosa, che si ottiene al moto. L’equazione del moto, considerando tale forza, è ancora lineare.

4.7.2.1 Vibrazioni libere

  Si consideri il modello rappresentato in fig.4.23; esso è quello di fig.4.14 al quale è stato aggiunto uno smorzatore oleodinamico. Quest’ultimo (v. fig.4.23,b) è costituito da un cilindro pieno di un fluido viscoso (generalmente un olio minerale). Nel cilindro scorre un pistone nel quale sono ricavati dei fori di piccolo diametro. Quando il pistone si muove nel cilindro il fluido passa da una camera all’altra attraversando i fori calibrati ricavati nel pistone. Il flusso è laminare perché i fori sono di piccolo diametro e per tanto la forza di attrito è proporzionale alla velocità.
La costante σ che lega la forza alla velocità è detta costante di smorzamento viscoso.
L’equazione del moto libero si scrive :

  Sostituendo l’integrale generale x(t) = nell’equazione del moto si ottiene:

m C l2 elt + s l elt + K C elt = 0

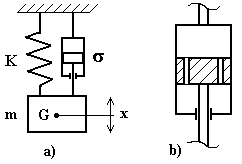
Fig.4.23
Dividendo tutti i termini per m e ricordando che  si ottiene:

e quindi:

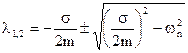
  E quindi la legge del moto è:

                        x(t) = C1elt  + C2elt                                                  (4.10)

  Le radici saranno reali, coincidenti o complesse a seconda che risulti:

                                                                                      (4.11)

  Si definisce smorzamento critico la quantità:

  Moltiplicando ambo i membri della (4.11) per σcr :

 

ossia:

                                                     (4.11’)

            Come si vede dalla (4.10) il moto del sistema è, in ogni caso, aperiodico e presenta caratteristiche differenti a seconda che lo smorzamento sia maggiore o minore di quello critico.

            1) σ > σcr
In questo caso λ1 λ2 sono reali e negative. La (4.10) mostra che il moto libero tende asintoticamente a 0 per t che tende ad infinito, qualunque siano le condizioni iniziali.

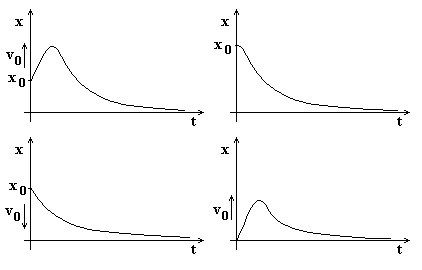
Fig.4.24

2) σ = σcr
Le due λ1 λ2 sono coincidenti:

-

per cui:

x(t) = (C1 + C2 t) e-ωnt 

Il moto del sistema è qualitativamente analogo a quello riportato in fig.4.24.

3) σ < σcr
Le due λ1 λ2 sono complesse e coniugate:

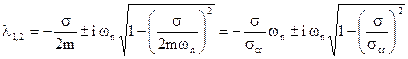
se si pone:

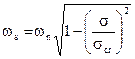
la legge del moto ha espressione:

che, per le formule di Eulero si può scrivere:

  Il moto del sistema è una vibrazione armonica di pulsazione ωs la cui ampiezza decresce nel tempo. Per questo motivo non si tratta di un moto armonico e neppure periodico, ma che si annulla periodicamente ad intervalli di tempo ; tale moto prende il nome di moto armonico smorzato. L’andamento di questo moto è rappresentato in fig.4.25.
Si dimostra che le curve di equazioni:

sono le curve in sviluppo della legge del moto.

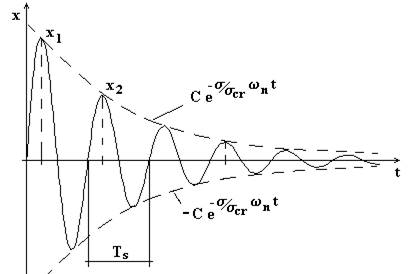
Fig.4.25

            Decremento logaritmico

  I due istanti t1 e t2 tali che t2 = t1 + Ts , i valori di x1 e x2 sono:

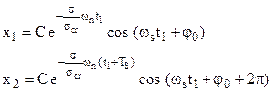
per cui:

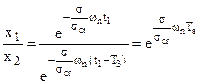
e quindi:
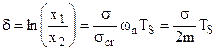                             (4.13)

  La quantità δ = ln(x1/x2) è detta decremento logaritmico ed ha una notevole importanza per lo studio del moto dei sistemi sui quali agisce uno smorzamento viscoso.
Se si dispone di una registrazione (del tipo di fig.4.25) la misura di Ts e di due massimi successivi, note le caratteristiche del sistema (massa e rigidità), consente di determinare lo smorzamento σ. Dalla (4.13) infatti:

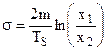
ovvero:

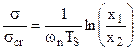
  E’ poi da osservare che in presenza di smorzamento viscoso risulterà:

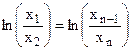                                                  (4.14)

  Se si calcolano i valori di δ per diverse coppie di massimi consecutivi essi dovrebbero risultare uguali; dunque, se si dispone della registrazione di un moto libero di un sistema reale,  un modello del sistema con attrito viscoso (del tipo rappresentato in figura 4.23) sarà tanto più aderante al sistema  reale  quanto più saranno prossimi i due membri della 4.14. Un valore medio del decremento logaritmico può essere calcolato con la seguente relazione:

            4.7.2.1 Vibrazioni forzate di sistemi con smorzamento viscoso

  Consideriamo ora un sistema come quello rappresentato in fig.4.23 sotto l’azione di una forza armonica che agisce sulla massa m (v. fig.4.26).

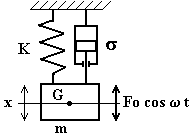
Fig.4.26

  L’equazione del moto è:

ossia:

  Come si è già detto a proposito dei modelli senza smorzamento (ora a maggior ragione) il moto del sistema è somma di un moto libero (destato dalle condizioni iniziali e dall’applicazione della forzante) e del moto forzato. Dopo il transitorio iniziale, a regime, il moto libero si estingue ed è presente solo il moto forzato:

                        x(t) » Xf cos (wt + j)

  L’equazione appena scritta rappresenta quindi un integrale particolare. La fase j, dal punto di vista analitico è resa necessaria dalla presenza del  termine; dal punto di vista fisico esprime il concetto per il quale lo spostamento (cioè l’effetto) è in ritardo rispetto alla forzante (la causa).
Sostituendo l’integrale particolare nella equazione del moto si ottiene:

- m w2 Xf cos (wt + j) - s w Xf sin (wt + j) +
+ K Xf cos (wt + j) = F0 cos wt                                             (4.15)

  In questa equazione sono contenute due incognite:
-    Xf, l’ampiezza del moto forzato a regime
-  j0 il ritardo con il quale lo spostamento raggiunge un massimo rispetto al massimo della forzante.

  Per ottenere le due incognite si scrive la (4.15) per due particolari istanti di tempo:

   I )     (wt + j) = 0          Þ   (K-mw2 Xf ) = F0 cos j                    (4.15’)
II)     (wt + j) = p/2    Þ     -s w Xf = -F0 sin j                           (4.15’’)

  Dal sistema di due equazioni appena scritte si ricava:

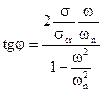
e

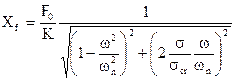
  Il primo termine a secondo membro è lo spostamento statico Xst ; il secondo è il coefficiente di amplificazione A in presenza di smorzamento. Dunque la relazione precedente si può scrivere, sinteticamente com’esegue:

Xf = Xst A

  In fig.4.27 è riportato l’andamento di A in valore assoluto in funzione del rapporto ω/ωn per diversi valori di σ/σcr.

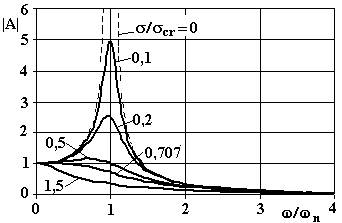
Fig.4.27

  Dalla fig.4.27 si può osservare che:
- All’aumentare dello smorzamento il coefficiente di amplificazione diminuisce ed il massimo si sposta in corrispondenza di valori di ω/ωn più bassi. Il valore per il quale si verifica il massimo di A è dato da:

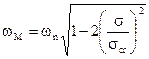
e risulta quindi più basso sia di ωn che di ωs . Per σ/σcr = 0,707 il massimo di A si ha per ω0 . Per valori maggiori del rapporto σ/σcr le curve non hanno più un massimo.
- Per piccoli valori del rapporto di smorzamento σ/σcr < 0,1, se ω non è prossimo a ωn , il comportamento dinamico del sistema è analogo a quello che si determina senza tener conto dello smorzamento.
In fig.4.28 è riportato l’andamento del ritardo di fase φ in funzione del rapporto ω/ωn per diversi valori di σ/σcr .   Da tale figura si può osservare quanto segue:
- Per ω/ωn = 1, qualunque sia il valore di σ , risulta φ = π/2.
- In assenza di smorzamento risulta: φ = 0 al disotto della risonanza e φ = π al disopra.
- Per piccoli valori del rapporto di smorzamento σ/σcr < 0,1, l’andamento di φ è simile a quello in assenza di smorzamento.

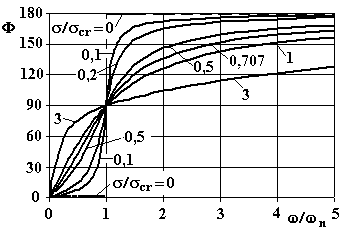
Fig.4.28

  Le forze che compaiono nell’equazione del moto (4.15) possono esser rappresentate graficamente come in fig.4.29.

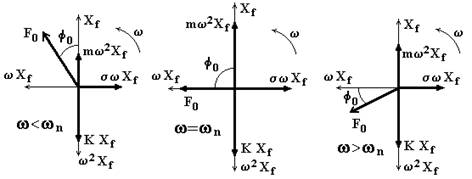
Fig.4.29

            Vibrazioni eccitate dal moto del vincolo

  Il moto forzato del sistema può essere destato anche dal moto del vincolo come mostrato in fig.4.30.

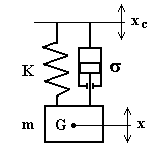
Fig.4.30

  In questo caso, detto  la posizione della massa rispetto a quella del vincolo, l’equazione del moto è:

ossia:

   Se il moto del vincolo è armonico: , la precedente equazione si scrive:

  Dunque il comportamento dinamico del sistema è quello che si ottiene considerando l’azione di una forza armonica di ampiezza:

e fase data da:

 

            4.7.3 Isolamento delle vibrazioni

  Il problema dell’isolamento delle vibrazioni si presenta in due modi differenti:
- Un sistema meccanico (ad esempio un gruppo di macchine) genera delle forze di inerzia le quali essendo forze esterne al sistema si scaricano sulla struttura di sostegno. Interponendo dei vincoli elastici si vuole limitare l’ampiezza forze trasmesse al basamento. Questo problema prende il nome di isolamento attivo.
- Un sistema (ad esempio uno strumento di precisione) poggia su di un basamento che vibra per una causa qualsiasi. Mediante l’interposizione di elementi elastici tra il basamento ed il sistema si vuole limitare che l’ampiezza della vibrazione della struttura di sostegno si trasmetta integralmente al sistema. Questo problema prende il nome di isolamento passivo. In entrambi gli aspetti, una massa sospesa mediante vincoli deformabili ha sei gradi di libertà, come mostrato in fig.4.31.
Tuttavia lo studio del problema mediante modelli ad 1 grado di libertà quali quelli rappresentati nelle figure 4.32 e 4.34 consente di ottenere risultati molto utili alla comprensione del problema stesso ed, in alcuni casi, applicabili direttamente.

Fig.4.31

 

            Isolamento attivo

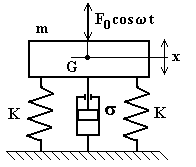
Fig.4.32

  In fig.4.32 è rappresentato un modello ad 1 g.d.l. relativo al problema dell’isolamento attivo delle vibrazioni. L’unico moto del sistema è quello verticale (moto di rimbalzo). Consideriamo l’azione di una forza armonica l’equazione del moto del sistema è quella già nota:

  Alla struttura si trasmette una forza Ft attraverso le molle e gli smorzatori; pertanto essa è il risultante di due forze: una di ampiezza KX che si trasmette per l’elasticità dei vincoli elastici ed una di ampiezza σωX che si trasmette a causa dello smorzamento.
Tali forze sono in quadratura, come mostrato in fig.4.29, per cui il loro risultante è:

  L’efficacia del sistema di sospensione è quantificata da un parametro detto coefficiente di trasmissibilità definito come rapporto tra l’ampiezza della forza trasmessa e l’ampiezza della forzante:

         deve risultare < 1

ricordando che , risulta:

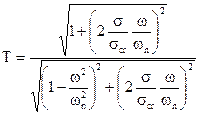
  In fig.4.33 è rappresentato l’andamento di  in funzione di ω/ωn per diversi valori del parametro σ/σcr . Dalla figura si osserva essenzialmente quanto segue:

- Per ottenere che sia T<1 occorre che sia ω/ωn>, qualunque sia il valore dello smorzamento.
- Per ω/ωn>, all’aumentare dello smorzamento T aumenta. Ciò può essere interpretato considerando che lo smorzatore costituisce un mezzo attraverso il quale la forza si trasmette al basamento.

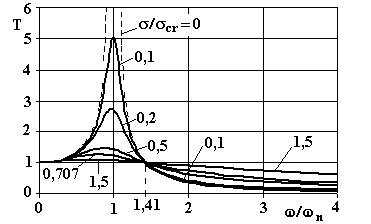
Fig.4.33

  Gli elementi elastici possono essere realizzati con i seguenti materiali:
Acciaio (molle ad elica, molle a tazza ecc.); Gomma; Sughero; Feltro
Ognuno di questi materiali può essere utilizzato in un campo di valori della pulsazione naturale del sistema, come riportato nella tabella che segue.

Tab. 4.I - Materiali per elementi elastici

wn (rad/s)	fn (Hz)	Materiale
7 - 14	1,1 – 2,2	Acciaio
14 - 18	2,2 – 2,85	Gomma
18 - 40,5	2,85 – 6,5	Sughero
40,5 -	6,5 -	Feltro

  Come si può osservare dalla tabella, non è possibile realizzare elementi elastici di sospensione che consentano di ottenere, per il sistema massa sospesa su elementi elastici, una pulsazione naturale più bassa di 7 rad/s. All’aumentare di ωn possono essere impiegati elementi elastici via via più economici.

            Isolamento passivo

  In fig.4.34 è rappresentato il modello ad 1 g.d.l. per il problema dell’isolamento passivo delle vibrazioni.


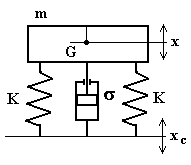
Fig.4.34
Se la struttura di sostegno del sistema avente massa m vibra con legge armonica:

l’equazione del moto del sistema è identica a quella vista a proposito delle vibrazioni forzate dal moto del vincolo:

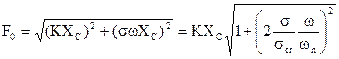
con:

  Nel caso di isolamento passivo, il coefficiente di trasmissibilità è definito come rapporto tra l’ampiezza del moto (forzato) della massa e quella della forzante: T = Xf/Xc . Ricordando l’espressione di Xf, risulta:

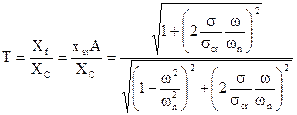
e cioè il coefficiente di trasmissibilità è identico a quello ricavato per l’isolamento attivo; valgono quindi le stesse considerazioni.
Nello studio fin qui illustrato, si sono fatte due ipotesi semplificative:
1) Si è considerato che la forza, nel caso di isolamento attivo, o la vibrazione della struttura di sostegno, nel caso di isolamento passivo, avessero andamento armonico.
2) Si sono presi in esame modelli ad un solo g.d.l.
Per quanto riguarda la prima ipotesi semplificativa, si ricordi che una grandezza periodica può esser vista come somma di termini armonici; per tanto si può concludere che l’effetto, in termini di trasmissibilità è dato dalla somma dei contributi dovuti alle singole armoniche. Occorre tener presente, però, che se il rapporto ω/ωn vale ad esempio 5 per la prima armonica, risulterà:

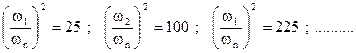
e così via. Cioè il contributo delle armoniche di ordine superiore alla fondamentale è trascurabile.
Per quanto riguarda la seconda ipotesi semplificativa, come già detto, una massa sospesa elasticamente ha sei g.d.l. e quindi le equazioni del moto costituiscono un sistema di sei equazioni differenziali.
Tuttavia se il sistema di sospensione elastica ha tre assi di simmetria, le sei equazioni sono indipendenti. Fisicamente ciò significa che ad ognuno dei moti che costituisce uno dei sei gradi di libertà del sistema, non si accoppia nessuno degli altri moti. In questo caso ognuno dei moti è descritto completamente da una sola equazione del tipo di quella riportata precedentemente e quindi di ognuno dei sei moti può essere studiato separatamente dagli altri applicando i risultati del modello ad 1 g.d.l.

Esempio 4.III:
Calcolo degli elementi elastici per un problema di isolamento passivo.
Uno strumento è montato su di un supporto che vibra con legge armonica; si desidera che tali vibrazioni non si trasmettano integralmente allo strumento stesso.
Sono noti:
La massa dello strumento m = 2Kg
L’ampiezza della vibrazione del supporto Xc = 2mm
La frequenza della vibrazione del supporto fc = 10 Hz
Il valore massimo dell’accelerazione alla quale strumento può essere sottoposto Amax = 5 x 10-3g
Si decide, innanzi tutto, di porre :

  Da cui:

quindi, la rigidità del sistema di sospensione sarà pari a:

K = m wn2 = 493,5 N/m

  Se si decide di adottare 4 elementi elastici disposti, in parallelo, come in fig.4.31 la rigidità di ciascuno di essi deve essere:

                        Ki = K/4 = 123 N/m

essendo fn = 2,5 Hz, dalla tabella 4.I si ricava che gli elementi elastici saranno tamponi di gomma.
Il moto forzato dello strumento montato su tali elementi elastici può essere calcolato con buona approssimazione trascurando lo smorzamento; quest’ultimo, infatti, si può ritenere piccolo rispetto a quello critico e la sua influenza si può ritenere minima essendo ω = 4ωn. Pertanto, l’ampiezza del moto forzato si può valutare sia pari a:

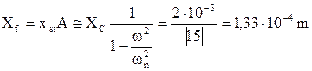
E l’ampiezza dell’accelerazione pari a:

 

4.8 Sistemi a DUE gradi di libertà

Lo studio dei sistemi a più gradi di libertà verrà affrontato facendo  riferimento, per semplicità, solo a sistemi conservativi, trascurando, cioè lo smorzamento.

4.8.1 Moto libero

Si esamina dapprima il moto libero del sistema, considerando, quindi, che su di esso non agisca nessuna forza esterna e che il moto sia imposto allontanando nell’istante iniziale le masse dalla loro posizione di equilibrio.
Consideriamo il sistema a due gradi di libertà ( x1 ed x2 ) rappresentato in fig. 4.35. Sulla massa m1 agiscono le seguenti forze:

• La forza di inerzia :
• La reazione della molla K1 :
• La reazione della molla K3 :

  Sulla massa m2 agiscono le seguenti forze:

• La forza di inerzia :
• La reazione della molla K2 :
• La reazione della molla K3 :

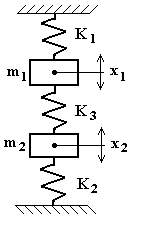
Fig. 4.35

Applicando in principio di d’Alembert, e cambiando segno  tutti i termini per comodità, le (due) equazioni del moto del sistema si scrivono:

  Ovvero:

  Coefficienti di rigidità
E’ utile definire i coefficienti di rigidità kij del sistema , il generico kij è definito come
- La reazione con segno cambiato che il sistema esercita sulla massa (o sulla sezione) i-esima per uno spostamento unitario della massa (o della sezione) j-esima, ferma restando tutte le altre masse (o sezioni). -
Dalla definizione di coefficienti di rigidità, per il sistema considerato risulta:

k11 = K1+K3               k22 = K2+K3              k12 = -K3 = k21

 

  Le equazioni del moto si possono allora scrivere nel seguente modo:

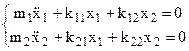                                    (4.16)

che costituiscono un sistema di equazioni differenziali lineari omogenee a coefficienti costanti.
L’integrale generale di tale sistema di equazioni è:

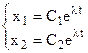
ma, per semplicità, supporremo direttamente che la soluzione sia di tipo armonico, per cui, nelle 4.15 sostituiremo l’integrale particolare:

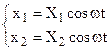                                                       (4.17)

  In altri termini, assumere che le 4.16 siano un integrale delle 4.16, significa supporre che sia possibile un moto per il quale ciascuna massa si muove con moto armonico di pulsazione w ed ampiezza Xi. Tale ipotesi risulta essere verificata nella realtà come si vedrà, anche, in alcuni degli esempi di applicazione.
Sostituendo l’integrale particolare 4.17 nelle 4.16 si ottiene:

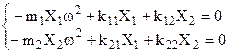                          (4.18)

che possono essere ordinate nel modo che segue:

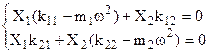                               (4.18’)

  Le 4.18 costituiscono un sistema di equazioni algebriche omogenee associate alle equazioni del moto; come è noto, affinché tale sistema ammetta soluzioni diverse da quella banale, è necessario che sia nullo il determinante D dei coefficienti delle incognite:

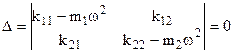
  E’ da osservare che se fosse D≠0 , si avrebbe la soluzione banale : X1 = X2 = 0 che fisicamente corrisponde ad assenza di moto.
Sviluppando tale determinante, si ottiene:

 ossia:

 e quindi una equazione biquadratica con due soluzioni doppie:

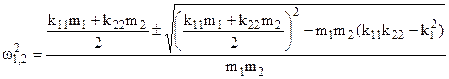                                                                                                                (4.19)

che rappresentano le due pulsazioni naturali del sistema.
Avendo imposto che sia D=0, le soluzioni sono diverse da quelle banali ma sono indeterminate (del tipo 0/0) per cui è possibile conoscere solo il loro rapporto X1/X2 che si può ottenere facilmente dalle 4.18’.
Dalla prima delle 4.17’:

                                          (4.20) 

  Sostituendo ciascuno dei due valori delle pulsazioni naturali (w1 ed w2) nella precedente equazione, si ottiene il rapporto fra le ampiezze delle vibrazioni delle due masse in corrispondenza di quella pulsazione. Se si sostituisce il valore più piccolo dato dalla 4.18 (cioè w1) si ottiene che X1/X2 > 0 ; se invece si sostituisce il valore più grande (cioè w2) si ottiene che X1/X2 < 0.

  Condizione di normalizzazione
Poiché non sono note le ampiezze ma solo il loro rapporto, per rappresentare le deformazioni del sistema che vibra con ciascuna delle due pulsazioni naturali, si stabilisce una condizione di normalizzazione.
La più semplice condizione di normalizzazione consiste nell’assumere che l’ampiezza della oscillazione della prima massa sia uguale ad 1 e si calcola di conseguenza l’ampiezza della oscillazione della seconda massa. Un esempio è riportato in fig.4.36. In tale figura le linee che congiungono le estremità dei segmenti che rappresentano le ampiezze delle oscillazioni sono dette linee elastiche. Il generico termine Xi,j di quest’ultima rappresenta l’ampiezza di oscillazione della massa i-esima per il j-esimo modo di vibrare.
Come si può osservare dalla fig.4.36, in corrispondenza della più bassa delle due pulsazioni naturali del sistema le due masse oscillano muovendosi entrambe nello stesso verso, mentre in corrispondenza della più alta delle due pulsazioni naturali del sistema le due masse oscillano muovendosi in verso opposto. Di conseguenza in corrispondenza della pulsazione più elevata la linea elastica presenta un punto che non si sposta, tale punto è detto nodo; in fig.4.36 il nodo è evidenziato da un cerchietto ed è indicato con n.
Da quanto detto si evince che:

• Un sistema a due gradi di libertà ha due pulsazioni naturali che individuano due modi di vibrare. Ciascuno di questi ultimi è rappresentato da una linea elastica del tipo riportato in fig.4.36.
• Il primo modo di vibrare (quello a pulsazione più bassa) presenta una linea elastica senza nodi, mentre il secondo modo di vibrare presenta un nodo.

  La circostanza per la quale le ampiezze delle vibrazioni non sono note, fisicamente, dipende dal fatto che il moto del sistema è un moto libero e pertanto è destato dalle condizioni iniziali, solo se queste ultime sono assegnate è possibile calcolare le ampiezze delle vibrazioni libere.

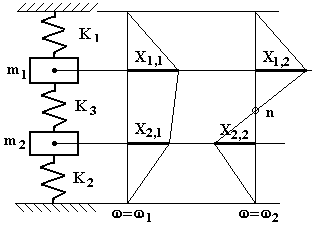
Fig.4.36

  Le equazioni 4.16 possono essere scritte in forma matriciale:

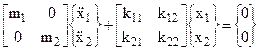
  Si dimostra che gli autovalori {wi}e gli autovettori [uij] della matrice [A] :

                        [A] = [M]-1 [k i,j]

rappresentano rispettivamente i quadrati delle le pulsazioni naturali del sistema e le ampiezze di oscillazione a meno di una costante arbitraria.
E’ da precisare che il primo pedice del generico termine uij si riferisce alla massa ed il secondo pedice riferisce al modo di vibrare; in altri termini, ciascuna delle colonne della matrice degli autovettori rappresenta la linea elastica del sistema per j-esimo modo di vibrare.

Esempio 4.I:
Il sistema rappresentato in fig. 4.35 ha le seguenti caratteristiche:
m1=2 kg ;  m2=5 kg ; 
K1=20000 N/m ;  K2=40000 N/m ;  K3=30000 N/m ;
Si desidera calcolare le pulsazioni naturali e le linee elastiche.

Si calcolano, innanzi tutto, i coefficienti di rigidità:

  k11 = K1+K3 = 5·104 N/m               k22 = K2+K3 = 7·104 N/m                
k12 = k21 = -K3 = -3·104 N/m

  Si scrive ora il sistema di equazioni del moto:

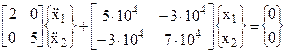
  Si calcolano autovalori ed autovettori della matrice:

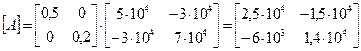
e si ottengono quindi:

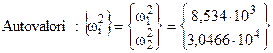
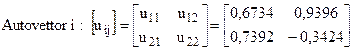
  Le pulsazioni naturali si ottengono come radici quadrate degli autovalori:

                        w1 = 92,38 rad/s
w2 = 174,55 rad/s

  Se si impone la condizione di normalizzazione u1j=1, le ampiezze delle linee elastiche dell’altra massa si calcolano come rapporto tra l’autovettore u2j e l’autovettore u1j :

  Primo modo di vibrare w=w1:
X1,1= 1   ;        X2,1= u2,1/ u1,1 = / = 1,098.

 Secondo modo di vibrare w=w2:
X1,2= 1   ;        X2,2= u2,2/ u1,2 = / = -0,364

  Le linee elastiche sono mostrate in fig. 4.37.
E’ possibile controllare che i risultati siano coretti applicando, con criterio, quanto è noto dallo studio dei sistemi ad 1 g.d.l. (grado di libertà). Per il secondo modo di vibrare, se sulla linea elastica si osservano i due triangoli che hanno il nodo come vertice comune, si può ricavare che il nodo stesso si trova sulla molla K3 ad una distanza pari a 1/(1+0,364) =  0,733 la sua lunghezza dalla massa 1, ovvero ad una distanza pari a 0,364/(1+0,364) = 0,267 della sua lunghezza dalla massa 2. Per quanto detto a proposito della sezione nodale, il sistema che oscilla nel secondo modo di vibrare può essere quindi considerato come formato da due sottosistemi:

• un primo sottosistema costituito dalla massa m1 cui sono collegate due molle (in parallelo) una delle quali di rigidità K1 e l’altra di rigidità K3/0,733 = 40928 N/m, per una rigidità complessiva pari a : K’= 20000 + 40928 = 60928 N/m.
• un secondo  sottosistema costituito dalla massa m2 cui sono collegate due molle (in parallelo) una delle quali di rigidità K2 e l’altra di rigidità K3/0,267 = 1127782 N/m, per una rigidità complessiva pari a : K’’= 40000 + 113636 = 153636 N/m.

 

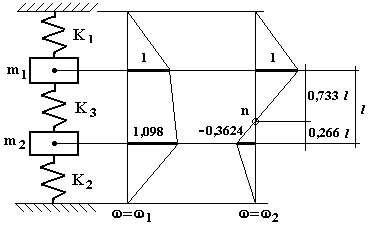
Fig. 4.37

Pertanto, per il primo sottosistema si calcola una pulsazione naturale pari a:

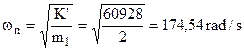
e, per il secondo sottosistema si calcola una pulsazione naturale pari a:

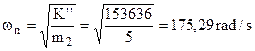
  A meno di errori numerici, le due pulsazioni sono identiche tra loro e coincidono con quella del secondo modo di vibrare.
Si è detto che le oscillazioni delle masse possono essere armoniche con pulsazione w1 oppure w2. Tali oscillazioni sono destate dalle condizioni  iniziali cioè dagli spostamenti iniziali X1(0) ed X2(0) e/o dalle velocità iniziali V1(0) ed V2(0). Se il rapporto tra le condizioni iniziali è uguale al rapporto tra gli autovettori relativi al j-esimo modo di vibrare, cioè se:

X1(0) / X2(0) e/o V1(0) / V2(0)= u1,j/ u2,j 

allora le condizioni iniziali destano solo il modo di vibrare j-esimo e le masse si muoveranno di moto armonico con pulsazione e con una linea elastica rappresentata dalla j–esima colonna della matrice [uij]. Tale comportamento si verifica anche se entrambe gli spostamenti iniziali sono nulli, mentre il rapporto tra le velocità iniziali soddisfa la condizione sopra riportata oppure se entrambe le velocità iniziali sono nulle, mentre il rapporto tra gli spostamenti iniziali soddisfa la condizione sopra riportata.
Se invece le condizioni iniziali sono qualsiasi, ciascuna massa si muoverà con un moto che è dato dalla soma di tutti i modi di vibrare (destati, ciascuno, con ampiezza diversa). Pertanto (cfr. somma di moti armonici diretti secondo lo stesso asse), se il rapporto tra le pulsazioni dei modi di vibrare è un numero razionale, il moto di ciascuna massa sarà periodico; se il rapporto tra le pulsazioni dei modi di vibrare non è un numero razionale, il moto di ciascuna massa sarà aperiodico.

4.8.2 Sistemi semidefiniti

  Si consideri il sistema rappresentato in fig. 4.38, per tale sistema i coefficienti di rigidità del sistema valgono:

k11 = k22 = K  ;           k12 = k21 = - K

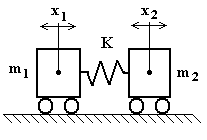
Fig. 4.38

  Le equazioni algebriche associate alle equazioni del moto si scrivono:

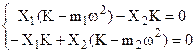                      (4.18’’)

 
Imponendo che sia D=0, si ottiene:

ossia:

                       

 

   Tale equazione consente di calcolare i valori delle due pulsazioni naturali:

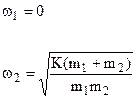
  La 4.19 consente di determinare le linee elastiche:
Primo modo di vibrare:

                       

 Secondo modo di vibrare:

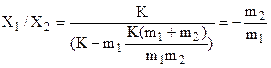
  In definitiva, si ottiene che:

• il primo modo di vibrare è caratterizzato dall’essere : w1=0 ed X1 =X2. Ciò può essere interpretato fisicamente come segue:

  Se si impongono condizioni iniziali congruenti con questa linea elastica, e cioè si spostano le due masse di quantità identiche dalla loro posizione di equilibrio (X1(0) = X2(0) ) e/o si impongono uguali velocità iniziali (V1(0) ed V2(0) ) , nessuna forza di richiamo agisce sul sistema che quindi si porterà in una nuova posizione di equilibrio e dunque non ritornerà mai nella posizione di equilibrio precedente. Il periodo di tale “oscillazione rigida” è quindi infinito e, di conseguenza, la pulsazione è nulla. Questo comportamento è proprio di tutti i sistemi ad estremi liberi o semidefiniti, quei sistemi, cioè, per i quali se le masse vengono allontanate di quantità identiche dalla loro posizione di equilibrio nessuna forza di richiamo agisce sul alcuna massa del sistema stesso.
- il secondo modo di vibrare è caratterizzato da una linea elastica per la quale la posizione del nodo è più vicina alla massa più grande, ciò tanto più quanto maggiore è il rapporto massa maggiore/massa minore.

4.8.3 Moto forzato

  Si consideri che sulla massa m1 agisca una forza armonica F0 cos wt, come rappresentato in fig.4.39.
Le equazioni del moto si possono scrivere nel seguente modo:

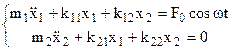                         (4.21) 


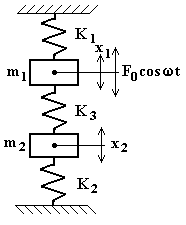
Fig.4.39

L’integrale generale di tale sistema di equazioni è:

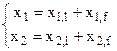
  Le precedenti relazioni mostrano che l’integrale generale è somma di due termini: xl che rappresenta l’integrale generale delle equazioni omogenee e quindi, fisicamente, il moto libero ed xf che rappresenta l’integrale particolare, ossia il moto forzato.
Se su di un sistema lineare agisce una forzante armonica di pulsazione w, a regime, (ossia dopo un transitorio iniziale) il sistema stesso oscillerà  con un moto armonico avente la stessa pulsazione w della causa forzante. Pertanto nelle 4.21 sostituiremo l’integrale particolare:

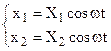                                                       (4.16)

  Si ottiene così:

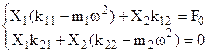                               (4.22)

  Indicando con D il determinante del sistema di equazioni 4.22:

                     (4.23)

si possono calcolare le ampiezze di oscillazione:

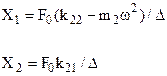                                         (4.24)

  In fig. 4.40 è rappresentato l’andamento qualitativo delle ampiezze delle oscillazioni di un sistema a 2g.d.l. al variare della pulsazione w della forzante.
Dalla figura si può osservare quanto segue:

• le ampiezze delle oscillazioni tendono ad infinito (si è trascurato lo smorzamento) per w= w1 e per w = w2. Ciò è evidente dalle 4.23 e 4.24, essendo i valori delle pulsazioni naturali quelli per i quali si annulla il determinante dei coefficienti.
• Esiste un valore della pulsazione w* della forzante per la quale risulta X1=0 ossia la massa sulla quale agisce la forzante è ferma.

 

  Il valore w* della pulsazione della forzante per il quale risulta X1=0 si può facilmente ottenere dalla prima delle 4.23:

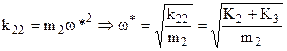                       (4.25)

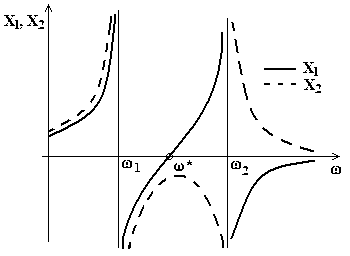
Fig.4.40

 

4.8.4 Smorzatori dinamici

  L’ultima osservazione riportata nel paragrafo precedente trova applicazione negli smorzatori dinamici. Nella fig.4.41 è rappresentato schematicamente un sistema costituito da una massa m1 sulla quale agisce una forzante armonica e da una massa m2 (più piccola) collegata elasticamente alla prima.
Nota la pulsazione w della forzante, dalla 4.24 si evince che se il valore della massa m2 e delle rigidità che la collegano alla massa m1 sono tali che risulti:

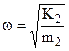
la massa 1 resterà ferma, mentre la massa 2 sarà l’unica ad oscillare.
Su tale principio vengono costruiti gli smorzatori dinamici. Il principio di funzionamento di questi ultimi si può riassumere come segue: ad una massa che si vuole impedire che vibri, si collega un’altra massa tramite un vincolo elastico tale da soddisfare la condizione data dalla 4.25.

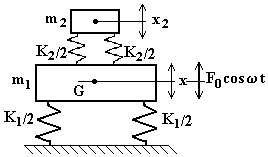
fig.4.41

Se tale condizione è rispettata, la massa che è stata aggiunta (la m2 nel caso considerato) oscillerà in controfase alla massa (m1) sulla quale agisce la forzante (essendo w1 < w* < w2) ed eserciterà sulla massa m1 una forza che istante per istante è uguale ed opposta alla F0coswt.

 

4.9 Cenni sui sistemi a più gradi di libertà

In generale per i sistemi a più gradi di libertà le equazioni del moto si possono ottenere applicando il principio di d’Alembert in modo analogo a quello visto per i sistemi ad 1 g.d.l. .

4.9.1 Moto libero

 Si consideri, ad esempio, il sistema a più gradi di libertà rappresentato in fig.4.42, trascurando le azioni smorzanti, le equazioni del moto per ciascuna massa si scriveranno:

Massa 1: 
Massa 2: 
……
……
Massa n: 

  Si ottiene quindi un sistema di n equazioni differenziali che costituisce il sistema di equazione del moto del sistema fisico considerato.
Se si utilizzano i coefficienti di rigidità del sistema kij , definiti nel paragrafo 4.8, per il sistema rappresentato in fig.4.42 risulterà:

k11 = K1+K2               k22 = K2+K3              k33 = K3+K4 
k12 = -K2 = k21              k23 = -K3 = k32          k13 = k14= k1n= 0      
……………                …………..                 …………..
……………                …………..                 knn = Kn-1+Kn

per cui, le precedenti equazioni si possono scrivere:

                       
                        (4.25)
…………..

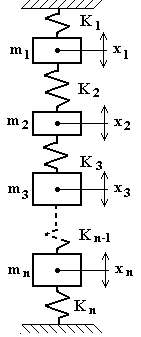
Fig. 4.42

Questo sistema si può scrivere in forma matriciale:

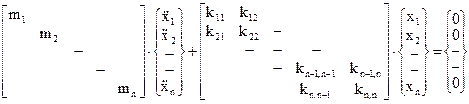
e, in forma simbolica:

  Come si può osservare quest’ultima equazione è formalmente analoga a quella vista per i sistemi ad 1 g.d.l. in assenza di smorzamento.
E’ ancora da osservare che, nell’esempio considerato, la matrice delle masse è diagonale e quella dei coefficienti di rigidità è tridiagonale; ciò è dovuto alla particolare struttura del sistema che viene detto ad accoppiamento elastico adiacente. Nel caso generale, invece, tali matrici contengono anche altri termini.
In generale le pulsazioni naturali e le linee elastiche si ottengono come già visto nel par.4.8.1., ossia come autovalori ed autovettori della matrice [A] :

                        [A] = [M]-1 [k i,j]

 

            Esempio 4.I:
Si consideri il sistema rappresentato in fig.4.43, per il quale sono assegnati i valori delle masse e delle rigidità delle molle:
m1=2 kg ;  m2=5 kg ;  m3=3 kg ;  m4=8 kg ; 
K1=20000 N/m ;  K2=40000 N/m ; K3=30000 N/m ;
K4=30000 N/m ;  K5=50000 N/m ;
Si desidera calcolare le pulsazioni naturali e le linee elastiche.

Si procede come visto per il sistema a 2 g.d.l.: si calcolano, innanzi tutto, i coefficienti di rigidità:

  k11 = K1+K3 = 5·104 N/m               k22 = K2+K3 = 7·104 N/m                
k12 = k21 = -K2 = -4·104 N/m         k13 = k31 = k14 = k41 = 0
k23 = k32 = -K3 = -3·104 N/m         k24 = k42 = 0
k34 = k43 = -K4 = -3·104 N/m
k33 = K3+K4 = 6·104 N/m               k44 = K4+K5 = 8·104 N/m

  Si scrive poi il sistema di equazioni del moto:

 

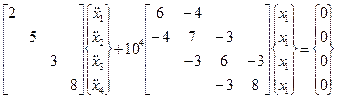
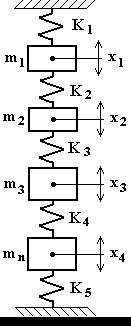
Fig.4.43

  Si calcolano autovalori ed autovettori della matrice:

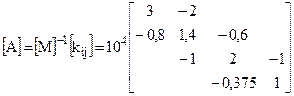
e si ottengono quindi:

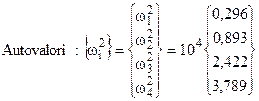
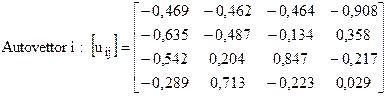
  Le pulsazioni naturali si ottengono come radici quadrate degli autovalori:

                        w1 = 54,41 rad/s
w2 = 94,48 rad/s
w3 = 155,66 rad/s
w4 = 194,66 rad/s

  Se si impone la condizione di normalizzazione u1j=1, le ampiezze delle linee elastiche delle altre masse si calcolano come rapporto tra l’autovettore uij (con i≠1) e l’autovettore u1j :

  Primo modo di vibrare w=w1:
X1,1= 1                                   ;           X2,1= u2,1/ u1,1 =1,36 ;
X3,1= u3,1/ u1,1= 1,16            ;           X4,1= u4,1/ u1,1 = 0,62 .

  Analogamente si procede per gli altri modi di vibrare.
Le linee elastiche sono mostrate in fig. 4.44.
Come si può osservare la linea elastica del primo modo di vibrare non ha nodi, quella del secondo ha 1 nodo, quella del terzo ha 2 nodi e quella del quarto ha 3 nodi. In generale, nelle linee elastiche dei sistemi ad n g.d.l., il numero di nodi è pari al numero del modo di vibrare meno 1.

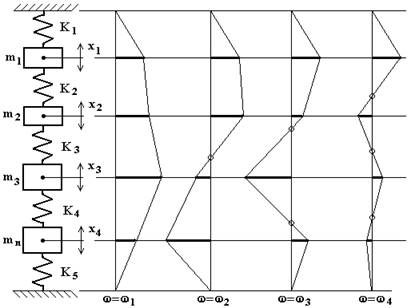
fig.4.44

 
4.9.2 Moto forzato

  Si consideri  che sul sistema rappresentato in fig.4.43 agiscono alcune forze armoniche, ciascuna di esse applicata su di una massa, di ampiezza Fi, ciascuna con una fase iniziale ji e tutte con la stessa pulsazione w. Le equazioni del moto si scrivono, in forma simbolica:

                      (4.26)

  Si dimostra (teorema di espansione) che le ampiezze delle oscillazioni forzate delle masse valgono:

                 (4.27)

dove uij sono gli autovettori e le hj(t) sono delle coordinate normali che consentono di risolvere il sistema di n equazioni in n incognite (4.26) come un insieme di n equazioni indipendenti. Si dimostra infatti che la generica hj(t) vale:

  Si osservi che la precedente relazione è formalmente simile a quella già vista per i sistemi forzati ad 1 g.d.l. . I termini che compaiono in tale relazione valgono:

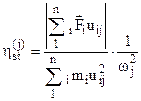
ed è detta ampiezza di equilibrio;

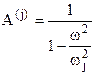
e rappresenta il coefficiente di amplificazione del modo di vibrare j-esimo, essendo wj la pulsazione di tale modo di vibrare. Infine, il termine y(j) rappresenta la fase del vettore risultante degli n vettori Fiuij, come mostrato in fig. 4.45.
In definitiva, quindi, risulta:

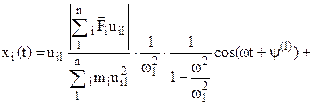
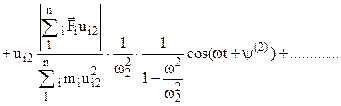
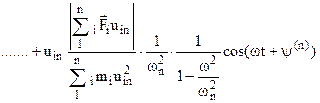
Tale relazione consente di calcolare la legge del moto di ciascuna massa.

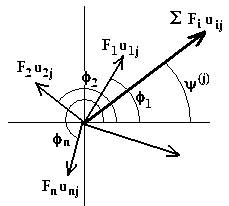
Fig.4.45