postulato di continuità

 

 

Il postulato di continuità

 

11-1 - Prime enunciazioni

Dopo aver effettuato una prima investigazione su come è "fatta" la "nostra" retta ordinaria, una domanda naturale che viene da porsi a questo punto è: ma quanti sono (nel senso della teoria dei numeri cardinali) i punti di  R  ?

   Come vedremo, la riposta non è semplice, e ci condurrà alla scoperta di una delle proprietà più riposte di quel concetto (lo "spazio" matematico) che verrà successivamente denominato appunto "continuo geometrico". Comunque, già sin d'ora potremmo dire, in accordo con la filosofia che ispira la presente esposizione: i punti della retta saranno tanti quanti se ne riescono (si è costretti) a concepire!

   Cominciamo prima di tutto con l'osservare che l'intelletto umano è costituito in modo da dover "vedere" infiniti punti di  R  , e ciò è un'immediata conseguenza delle considerazioni che ci hanno condotto a riconoscere la divisibilità del semigruppo  S (a partire da un dato segmento   , si consideri il suo punto medio  c , e quindi di nuovo il punto medio per esempio di   , ottenendo così una successione di punti distinti di  R  tutta all'interno del segmento prefissato, e quindi limitata) . Peraltro, Euclide stesso in uno dei suoi postulati (il secondo) ammetteva la prolungabilità di un segmento, proprietà che implica essa pure la possibilità di costruire successioni

p1, p2, p3, ...

di punti distinti di  R , in questo caso non limitate:

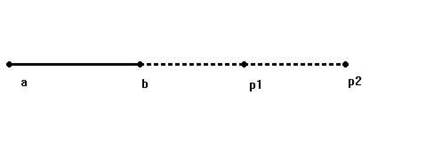
Fig. 11-1-1

[Il segmento    si prolunga nel segmento   , il segmento    nel segmento   , etc..]

   Nei termini che ci sono ormai familiari, possiamo cioè asserire la verità della seguente affermazione:

Teorema (11-1-2) -       ³  !0   .

   Naturalmente non possiamo essere del tutto soddisfatti della disuguaglianza (11-1-2), perché vorremmo sapere per esempio se risulta addirittura    =  !0 , oppure no, e se in tal caso    coincida con uno dei (pochi!) cardinali infiniti che conosciamo, vale a dire   2! , 2^(2!) , etc. (qui il simbolo ^ indica l'elevazione a potenza).

   Per andare avanti nell'analisi che intendiamo effettuare, non sono sufficienti le proprietà di  R  che abbiamo finora individuato, e dobbiamo formularne una nuova (adempimento peraltro consueto, laddove si abbia a che fare con problemi di esistenza, e qui si tratta proprio di riconoscere quanti punti della retta "esistono"), che avrà comunque sempre il suo fondamento nell'intuizione. A tale proprietà si dà il nome di postulato di continuità (della retta ordinaria), d'onde, come dicevamo dianzi, il termine "continuo geometrico".

   Prima di enunciare il postulato in oggetto, spendiamo qualche parola a dimostrare che di esso si trovano tracce sin nell'antichità, a riprova che esso appartiene in effetti al regno della descrizione, e non a quello dell'invenzione. Gli studenti che hanno avuto la ventura di capitare con un buon insegnante di filosofia, ricorderanno il celebre episodio di Socrate che cerca di dimostrare come chiunque sia in grado, grazie a quello che già sa, di risolvere un problema quale la duplicazione del quadrato (episodio narrato nel Menone di Platone). Per descrivere brevemente la situazione (che in realtà richiede, per essere descritta nel modo rigoroso che ci proponiamo costantemente come obiettivo, dei concetti che esamineremo più avanti, quando tratteremo di teoria della misura), si immagini un quadrato  Q , il cui lato possiamo supporre unitario, e di voler costruire un altro quadrato  Q'  la cui area sia doppia di quella di  Q , e pertanto uguale a  2 . Socrate comincia con l'osservare che il lato di  Q'  dovrà essere più grande di quello di  Q , ma che se si prende il doppio di questo si ottiene un quadrato  Q''  troppo grande rispetto a quanto si vuole, perché esso avrebbe manifestamente area quadrupla di quella di  Q :

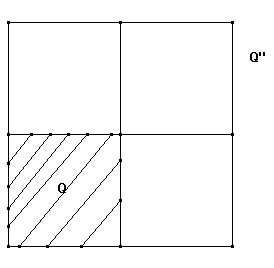
Fig. 11-1-3

   L'antico filosofo conduce quindi il suo interlocutore a comprendere come il quadrato richiesto sia esattamente quello costruito sulla diagonale di  Q :

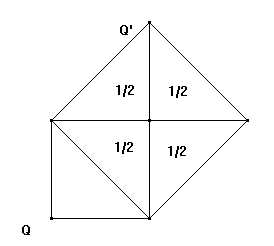
Fig. 11-1-4

ma non è tale costruzione che qui ci interessa, quanto piuttosto mettere in luce la circostanza che la ricerca di  Q'  già presuppone che esso esista, ovvero che esista un punto sulla retta che sia l'estremo del lato ricercato (l'altro estremo sarà a comune con il lato primitivo di  Q ). Orbene, quando si vanno ad analizzare le ragioni della nostra persuasione, cioè che tale punto esiste, è proprio con il postulato di continuità, e questioni connesse, che abbiamo in sostanza a che fare.

   Ciò premesso, come si può-deve enunciare il postulato che stiamo ricercando, avendo sempre presente l'ammonimento epistemologico-didattico di Galileo che abbiamo citato nell'Introduzione?

   Tra tante enunciazioni equivalenti, che pure presto introdurremo, una lunga esperienza ci conduce a scegliere la seguente:

PC - Fissato ad arbitrio - ma in modo inessenziale - uno dei due ordinamenti naturali di  R , si immagini in  R  un qualsiasi sottoinsieme di punti  X  che sia non vuoto e limitato (per il significato di questo termine si veda la sezione sull'ordine). Ciò equivale a dire che, detto  A  l'insieme dei minoranti di  X , esso non è vuoto, e superiormente limitato, mentre quello  B  dei maggioranti di  X  è pure non vuoto e inferiormente limitato. Orbene, l'intuizione geometrica conduce a riconoscere che  A  deve avere un massimo  mA  ( A  coincide con un semiretta inferiore chiusa -  mA  si dice l'estremo inferiore di  X ), così come  B  deve avere un minimo  mB  ( B  coincide con una semiretta superiore chiusa -  mB  si dice l'estremo superiore di  X ), ovvero che, qualora  X  non si riduca a un unico punto, esiste un minimo segmento contenente  X , il quale segmento coincide esattamente con   .

[Qui "minimo segmento" è inteso ovviamente con riferimento all'ordinamento parziale naturale di Segm(R).]

   PC si può manifestamente "spezzare" (poiché la scelta del verso di  R  è, come abbiamo specificato, inessenziale, e si può passare da un'orientazione all'opposta) in due enunciati equivalenti tra loro ed equivalenti a PC.

PC1 - Fissato ad arbitrio un verso di  R , comunque dato un sottoinsieme  A Ì R  non vuoto e superiormente limitato, esso ammette un estremo superiore, in simboli  sup(A) , ovvero un minimo maggiorante.

PC2 - Fissato ad arbitrio un verso di  R , comunque dato un sottoinsieme  A Ì R  non vuoto e inferiormente limitato, esso ammette un estremo inferiore, in simboli  inf(A) , ovvero un massimo minorante.

[Come pure dire che l'intuizione geometrica forza a ipotizzare un'esistenza di taluni enti che sarebbe più congrua in un contesto di "buon ordinamento", ma è appena il caso di ripetere che gli ordinamenti naturali della retta non costituiscono affatto dei buoni ordinamenti!]

[A prescindere dalla menzionata possibilità di invertire il verso di  R , è logicamente dimostrabile che PC1 e PC2 sono equivalenti, e alla circostanza vogliamo dedicare qualche esplicita considerazione, perché istruttiva al fine di comprendere bene i concetti di cui trattasi. Resta il fatto però che, al di là appunto dell'aspetto logico della questione, la situazione appare chiarissima dal punto di vista dell'intuizione geometrica. Supponiamo per esempio che valga PC1, e dimostriamo che un sottoinsieme  A Ì R  non vuoto e inferiormente limitato ammette un estremo inferiore  inf(A) . Introduciamo all'uopo l'insieme  M  dei minoranti di  A , il quale risulta non vuoto e superiormente limitato per ipotesi. Possiamo quindi introdurre il punto  m = sup(M) , certo esistente in virtù di PC1, e dimostriamo che si verifica invero  m = inf(A) . Per dimostrare quest'ultima identità, e cioè che  m  è il massimo dei minoranti di  A , bisogna dunque provare: uno, che  m  è un minorante di  A ; due, che  m  è il massimo di tali minoranti. Quanto alla prima asserzione, se  $ a Î A , a < m , allora sarebbe pure  M £ a < m , e  m  non potrebbe essere un estremo superiore per  M (ovvero, il minimo dei maggioranti di  M : il punto  a  risulterebbe un maggiorante di  M  minore di  m ). Quanto alla seconda, se  $ m' Î M , m < m' , ecco che  m  non sarebbe allora un maggiorante di  M , qed.]

   In parole "semplici", PC significa che non è possibile concepire un sottoinsieme limitato costituito da più punti della retta senza immaginare, non solo un segmento nel quale esso è contenuto (che è la definizione stessa di sottoinsieme limitato), ma anche un minimo tale segmento (nei casi PC1 e PC2, una minima semiretta chiusa, rispettivamente inferiore e superiore).

[Nel caso dianzi ricordato di Socrate, PC si può utilizzare per dimostrare l'esistenza del lato ricercato al seguente modo. Diciamo    il lato unitario di partenza, e orientiamo la retta da  a  verso b . Consideriamo poi tutti i punti  x  , sulla semiretta aperta superiore di vertice  a , tali che il lato    corrisponda a un quadrato di area minore di due. E' chiaro che si ottiene così un sottoinsieme  X  superiormente limitato (il doppio del lato di partenza è "troppo"), e che il lato del quadrato di area 2 è esattamente   , dove  z  designi l'estremo superiore di  z . Lo studente diligente che andasse a provare dettagliatamente la verità di questo asserto scoprirebbe che in realtà tale dimostrazione non è immediata, e che tra i "presupposti" di essa c'è la circostanza che la "funzione" area è continua, - ovvero, che se un quadrato ha area minore di una quantità data, è possibile pensare un quadrato che abbia area maggiore della precedente, ma ancora minore della quantità data, più l'analogo asserto nel caso di un'area maggiore - tutte nozioni di cui ci dovremo più estesamente e precisamente occupare. Il successivo teorema 11-4-1 ha in effetti ancora a che fare con la questione, che, ripetiamo, si potrà però considerare completamente risolta solamente dopo l'introduzione dei numeri reali, e di un'adeguata teoria della misura per le superficie, ancorché di tipo "semplice".]

   Altre forme assai comuni nelle quali si può trovare espresso il PC sono le seguenti.

PC3 - Sia  s1 Ê s2 Ê s3 Ê ...  una successione monotona decrescente di segmenti di  R . L'intersezione di tutti i segmenti in oggetto non può essere vuota.

[Si noti che è qui essenziale che si tratti di segmenti di  R , ovvero di sottoinsiemi di  R  i quali, rispetto a un fissato verso di  R , siano intervalli chiusi e limitati. Trovare un controesempio nel caso di intervalli aperti, o non limitati, sarebbe del tutto ovvio.]

PC4 - Fissiamo ancora una volta per comodità, ma ad arbitrio, un verso di  R , e diciamo che una coppia ordinata  (A,B)  di sottoinsiemi non vuoti di  R  costituisce una coppia di classi contigue se: (i)  A £ B  (il che significa ovviamente: " a Î A , " b Î B  Þ a £ b - A si dice in tali condizioni, e con relazione al prefissato verso di  R , la classe inferiore della coppia, e B quella superiore); (ii) A  e  B sono indefinitamente vicine, il che si esprime richiedendo che, " segmento libero  s Î S , esistono due punti  a Î A , b Î B  tali che
ab < a  (ovvero, che esiste un rappresentante  s  di  s  contenente al proprio interno  a  e  b ,  Ì s ). Orbene, una coppia di classi contigue ammette sempre un (ovviamente unico) elemento di separazione, vale a dire, esiste uno ed un sol punto  p  tale che:  A £ p £ B .

[Esempi di classi contigue sono ovviamente numerosissimi, dal caso più banale, minimale, in cui  A  e  B  si riducono allo stesso punto, a quello massimale (la terminologia è giustificata dalla circostanza che nell'insieme delle classi contigue di  R  si può introdurre un relazione d'ordine parziale naturale: (A,B) £ (A',B') se e soltanto se  A Í A', B Í B' ), in cui  A  e  B  sono due semirette chiuse con la medesima origine (si noti che non si è richiesto esplicitamente nella definizione che i due sottoinsiemi  A, B  siano disgiunti, caso che può pure invero verificarsi). Anche due semirette aperte con la medesima origine forniscono un esempio di classi contigue, adesso disgiunte, di cui il comune vertice è l'elemento di separazione. Siamo qui di fronte a un esempio di sezione di  R , con il quale termine si indica una coppia di classi contigue disgiunte massimale (nell'insieme delle coppie di classi contigue di tale particolare tipo!). Il PC si può esprimere anche dicendo che una sezione  (A,B)  di  R  non può mai essere tale che  A È B = R , anzi, che in tale caso esiste un (unico) punto  p Î R  tale che  A È B = R - {p} , o anche che l'esempio di una coppia di semirette aperte aventi la medesima origine è il solo caso di sezione della retta. Il caso forse più celebre di coppia di classi contigue (e tanti altri simili ne incontreremo trattando di teoria della misura) è dato dalla cosiddetta rettificazione della circonferenza. Si immaginino invero una circonferenza, e rispetto ad essa due poligoni  P  e  P'  rispettivamente inscritto e circoscritto, e si costruiscano due segmenti   ,  , i quali, con riferimento a un punto  o  scelto ad arbitrio, e "dalla stessa parte" della retta, rappresentino lo sviluppo lineare di  P  e di  P' , con palese significato dei termini. Orbene, i due insiemi, al variare di  P  e  P',  A = {p} , B = {p'}, costituiscono una coppia di classi contigue, il cui elemento separatore  z  è tale che il segmento    "rettifica" appunto la circonferenza - la sua "misura", supponendo per esempio il raggio della circonferenza unitario, è il famoso  2p .]

 

11-2 - Conseguenze dinamiche

   Le cinque enunciazioni precedenti del postulato di continuità hanno un carattere che possiamo definire statico. Eccone invece delle conseguenze (come prima, le dimostrazioni assai facili si lasciano al lettore) di carattere dinamico (e non si ritengano incongrui questi termini nel presente contesto, tenuto conto di quanto si è affermato in precedenza in ordine ai rapporti tra l'insieme dei numeri naturali  N  e il tempo), pur esse equivalenti tra di loro.

Teorema (11-2-1) - Fissato al solito un verso di  R , comunque data una successione  f  di punti di  R : p1, p2, p3, ... , che sia monotona crescente e superiormente limitata, allora essa convergerà verso il proprio estremo superiore (cioè, verso l'estremo superiore del codominio della successione).

Teorema (11-2-2) - Fissato al solito un verso di  R , comunque data una successione  f  di punti di  R : p1, p2, p3, ... , che sia monotona decrescente e inferiormente limitata, allora essa convergerà verso il proprio estremo inferiore (cioè, verso l'estremo inferiore del codominio della successione).

Teorema (11-2-3) - Fissato al solito un verso di  R , comunque data una successione  f  di punti di  R : p1, p2, p3, ... , che sia limitata, allora si possono introdurre le seguenti successioni:

a1 = estremo inferiore di  f
a2 = estremo inferiore di  f  ristretta al complementare di  s1
(ovvero, la successione p2, p3, p4, ...)
a3 = estremo inferiore di  f  ristretta al complementare di  s2
(ovvero, la successione p3, p4, p5, ...)
etc.

b1 = estremo superiore di  f
b2 = estremo superiore di  f  ristretta al complementare di  s1
b3 = estremo superiore di  f  ristretta al complementare di  s2
etc.

le quali successioni risultano, ovviamente, la prima monotona crescente (e superiormente limitata), la seconda monotona decrescente (e inferiormente limitata). Detti allora  a  il limite della prima, e  b  il limite della seconda, essi si chiamano rispettivamente il minimo e il massimo limite di  f  (in simboli,
a = minlim f , b = maxlim f), e  f  è convergente se, e soltanto se,  a = b  (questo punto coincide con il limite di  f ). Da  f  si possono sempre estrarre una sottosuccessione convergente ad  a , ed una convergente a  b , mentre se si prende in generale una sottosuccessione di  f  convergente allora il suo limite  z  sarà compreso fra  a  e  b . Se  f  converge, allora ogni sottosuccessione di  f  è convergente, e verso lo stesso limite di  f .

[Nei corsi di Analisi si impara ad usare un enunciato che generalizza il precedente teorema al caso delle successioni non limitate, introducendo i "limiti", e in corrispondenza gli estremi, di sottoinsiemi non limitati, in simboli:  +¥  e  - ¥ .]

   Con gli enunciati di cui sopra abbiamo utilizzato nozioni proprie della struttura topologica della retta. Un'analisi più approfondita di tali strutture viene offerta dai corsi di Analisi, ma qui ci sembra opportuno dare comunque alcuni cenni di tale studio, soprattutto dal punto di vista della relativa nomenclatura, e in vista di due importanti nuove formulazioni di PC.

 

11-3 - Interludio topologico

Una struttura topologica su un dato insieme, che si chiamerà ancora una volta il sostegno (o supporto) della struttura (o spazio topologico), è "qualcosa" che ci permetterà di introdurre in quell'insieme le nozioni di limite (di successioni) e di continuità (di funzioni tra spazi topologici), le quali si fondano su una nozione di "vicinanza" che viene specificata con l'introduzione del concetto di intorno. Si tratta di strutture di cui solo in tempi recenti (all'inizio del XX secolo) si è compresa la rilevanza nei fondamenti della matematica, e che vengono tradizionalmente considerate in una famiglia a parte rispetto alle strutture algebriche e d'ordine, anche se volendo le si potrebbe riguardare tra le prime (una topologia sull'insieme  A  può essere concepita come un'operazione unaria interna non in  A , bensì in  P(A) , soddisfacente a certi determinati assiomi - l'operazione è quella che associa a un sottoinsieme  X Í A  la sua chiusura   , approccio di Kuratowski alla topologia).

   Noi preferiremo operare in un modo più "tradizionale", cominciando con l'introdurre la nozione di intorno di un punto  p  della retta  R  al seguente modo: un sottoinsieme  X Í R  si dice un intorno di  p  se  X ' p , e se, oltre a  p , esso contiene un intero segmento di  R  avente centro in  p . Ovviamente, l'intersezione di intorni risulta ancora un intorno, e ogni sottoinsieme contenente un intorno di un punto risulta egli stesso un intorno di quel punto.

[Tale definizione si estende al piano ed allo spazio ordinario considerando, anziché segmenti, per esempio cerchi, o quadrati, e sfere (solide) o cubi, sicché tutti gli enti geometrici fondamentali risultano essere il supporto di strutture topologiche "naturali", mentre non altrettanto può dirsi, come abbiamo visto, per strutture algebriche o d'ordine.]

   Data la nozione di intorno, si dirà che un sottoinsieme  X Í R  è aperto se esso risulta intorno di ogni proprio punto, e chiuso invece se il suo complementare (si intende in  R) risulta aperto. Notiamo che tali definizioni hanno il merito di corrispondere alle analoghe di cui siamo già in possesso in conseguenza della teoria dell'ordine, sicché un intervallo di  R  (una volta che si sia fissato su di essa uno dei due versi) sarà in effetti aperto o chiuso in accordo con questa nuova definizione, e così pure per il caso delle semirette (inferiori o superiori).

   Si scopre facilmente che in  R  esistono sottoinsiemi che sono aperti, altri che sono chiusi (non potendosi escludere che qualcuno possa essere al tempo stesso chiuso e aperto, come è per esempio il caso dell'intera retta  R , dal momento che, in forza della definizione, l'insieme vuoto si deve considerare aperto), altri che non sono né aperti né chiusi. Inoltre, che un insieme  X  di  R  è un intorno di un suo punto  p  se e soltanto se contiene un sottoinsieme aperto di  R  il quale a sua volta contiene  p , sicché sarà possibile limitarsi spesso alla considerazione dei soli intorni aperti di un punto; che se consideriamo due qualsiasi punti distinti di  R , diciamoli  p  e  q , esisteranno un intorno di  p  e uno di  q  disgiunti (assioma di separazione di Hausdorff), etc..

   L'insieme  AR  degli aperti di  R  è un sottoinsieme di  P(R)  che soddisfa manifestamente alle seguenti proprietà:

(11-3-1) L'unione di una qualsivoglia famiglia di aperti è un aperto.

(11-3-2) L'intersezione di una famiglia finita di aperti è un aperto.

(11-3-3) Il sottoinsieme vuoto e  X  sono elementi di  AR  .

laddove quello dei chiusi, diciamolo  CR , soddisfa invece alle proprietà duali:

(11-3-1') L'intersezione di una famiglia finita di chiusi è un chiuso.

(11-3-2') L'unione di una qualsivoglia famiglia di chiusi è un chiuso.

(11-3-3') Il sottoinsieme vuoto e  X  sono elementi di  CR  .

   Ciò premesso, si perviene alla nozione astratta di spazio topologico chiamando tale ogni coppia ordinata costituita da un insieme  X , sostegno dello spazio (i cui elementi si diranno punti), e da un sottoinsieme  AX Í P(X)  , i cui elementi, che si diranno gli aperti di  X , soddisfano alle proprietà (11-3-1,2,3) (una definizione equivalente si otterrebbe scegliendo invece l'insieme dei chiusi  CX , e le proprietà con apice). E' chiaro come si dovrà dare in uno spazio topologico astratto la nozione di intorno di un punto, alla quale aggiungiamo le seguenti definizioni (e proposizioni, tutte però di immediata dimostrazione - più o meno!), che elenchiamo tanto per dare un'idea di cosa sia la topologia, e che non solo potranno introdursi nel caso di oggetti quali la retta, il piano ordinario, etc., ma anzi proprio in essi trovano la loro migliore illustrazione.

(11-3-4) Se  (X, AX)  è uno spazio topologico, e  Y  è un sottoinsieme di  X , un punto  p Î X  si dice un punto di aderenza per  Y  se ogni intorno di  p  contiene qualche punto di  Y .

(11-3-5) Se  (X, AX)  è uno spazio topologico, e  Y  è un sottoinsieme di  X , un punto  p Î X  si dice un punto di accumulazione per  Y  se ogni intorno di  p  contiene qualche punto di  Y  diverso da  p . L'insieme dei punti di accumulazione di  Y  si chiama il derivato di  Y , e pertanto lo si indica talora con il simbolo  ¶Y . Il derivato di un insieme  Y  è sempre un insieme chiuso.

[Manifestamente, un punto di accumulazione è sempre un punto di aderenza, ma non viceversa; inoltre, esso può appartenere oppure no ad  Y . Un punto di aderenza che non sia un punto di accumulazione è necessariamente un punto di  Y , ed è quello che si dice un punto isolato di  Y .]

[E' forse opportuno rammentare qui un importante Teorema di Bolzano, ulteriore conseguenza del postulato di continuità: Un sottoinsieme infinito e limitato della retta  R  ammette sempre almeno un punto di accumulazione.]

(11-3-6) Se  (X, AX)  è uno spazio topologico, e  Y  è un sottoinsieme di  X , un punto  p Î X  si dice un punto di frontiera per  Y  se ogni intorno di  p  contiene tanto qualche punto di  Y , quanto del complementare di  Y  (in  X). La frontiera di  Y , che indicheremo con  Fr(Y) , è per definizione l'insieme dei punti di frontiera di  Y , e risulta sempre un insieme chiuso

(11-3-7) Se  (X, AX)  è uno spazio topologico, e  Y  è un sottoinsieme di  X , si dice chiusura di  Y , e la si indica con il simbolo  , il sottoinsieme costituito da tutti i punti di aderenza di  Y .   risulta un chiuso di  X , ed è precisamente il minimo chiuso di  X  contenente  Y  (nel senso che se  C  è un sottoinsieme chiuso di  X  contenente  Y , allora  C Ê . Inoltre, risulta:

 = Y È ¶Y = Y È Fr(Y) .

(11-3-8) Se  (X, AX)  è uno spazio topologico, e  Y  è un sottoinsieme di  X , si dice interno di  Y  l'insieme dei suoi punti interni, ovvero di quei punti di  Y  dei quali  Y risulta un intorno. Si chiama invece punto esterno ad  Y  un punto interno al suo complementare, e l'insieme di tali punti lo si dice l'esterno di  Y .

(11-3-9) Se  (X, AX)  è uno spazio topologico, e  Y  è un sottoinsieme di  X , si dice che  Y  è denso in  X  se ogni punto di  X  è un punto di accumulazione per  Y , ovvero se  X Í ¶Y . Naturalmente, in tal caso, risulta di necessità   = X . Y  si dice invece denso in sé se  Y Í ¶Y . Un sottoinsieme di  X  che sia denso in sé e chiuso lo si dice perfetto.

[Esempi di sottoinsiemi perfetti di  R  sono naturalmente, oltre ai banali  Æ  e  R  stessa, tutti i segmenti, e le semirette chiuse.]

   La topologia è quella branca della matematica che studia gli spazi topologici, che andranno anch'essi a costituire una grande categoria    che verremo presto a definire. Facciamo vedere subito invece come la nozione di topologia - ancorché troppo generale per avere teoremi particolarmente significativi (nel senso che limitarsi alle sole tre proprietà (11-3-1,2,3) rende la nozione di spazio topologico troppo "debole", e gli spazi topologici "troppi"), per ottenere i quali bisognerà aggiungere alle dette proprietà degli assiomi addizionali che specificheranno di volta in volta le particolari sottofamiglie di spazi oggetto di studio - consente di introdurre precisamente il concetto di limite di una successione di punti in uno spazio topologico, e quindi in particolare in  R .

[Che gli spazi topologici siano tanti, e di tipi assai diversi tra loro, è dimostrato anche dalla seguente considerazione, che dato uno spazio topologico  (X, AX) , e un suo qualunque sottoinsieme  Y , Y  eredita da  X , per il solo fatto di esservi contenuto, la struttura topologica (una tra le molteplici che in effetti  Y  possiede), tanto che si può non impropriamente parlare, anziché di sottoinsiemi, di sottospazi di  X . Tale topologia è semplicemente quella che dichiara aperti di  Y  le intersezioni degli aperti di  X  con  Y , e la si dice talora la topologia indotta per relativizzazione.]

   Sia dunque data un successione  f : N ® X  di punti di uno spazio topologico  (X, AX) , diciamola  x1, x2, x3, ... . Si dice che un punto  x0 Î X  è un limite di  f , se per ogni intorno  U(x0)  in  X  esiste un indice  kU Î N  (variabile in generale con la scelta di  U(x0) ) tale che  U(x0) ' xk  per tutti gli indici  k ³ kU  (ovvero tutti i punti della successione, da un certo punto in poi - o da un certo momento in poi, conformemente alla nostra interpretazione dinamica! - sono "vicini" al limite quanto io voglio).

   Dicevamo che la nozione di topologia è troppo generale, e ne abbiamo immediata riprova quando ci rendiamo conto che con essa non possiamo neppure dimostrare un teorema di unicità del limite, sicché possiamo parlare solo dell'insieme dei limiti di  f (eventualmente vuoto), e scrivere  x0 Î lim(f) , anziché  x0 = lim(f) . Un esempio, seppure assai banale, lo si trova subito considerando la topologia banale che dichiara unici aperti di  X  il vuoto e lo stesso  X (tale topologia minima la si dice la topologia condensata su  X ; al contrario quella massima, che dichiara aperti tutti i sottoinsiemi di  X , la si dice la topologia discreta su  X ). In questo caso infatti, comunque data una successione  f  di  X , ogni punto di  X  risulta un limite della successione! Si ottiene invece il desiderato teorema (e la dimostrazione è ovvia) quando si considerino per esempio i soli spazi topologici separati, ovvero quelli che soddisfano al sunnominato assioma di separazione di Hausdorff. Essendo invero la retta ordinaria, il piano, etc., spazi topologici separati, ecco che in tali casi la situazione si presenta "decente" come è auspicabile.

   Quello di Hausdorff non è l'unico "assioma di separazione" che è usuale introdurre in topologia, la questione anzi costituisce un interessante capitolo della disciplina, qualora si vogliano appunto separare, in modi più o meno "forti", punti da punti, o punti da chiusi, o chiusi da chiusi, etc.. Qui ci limiteremo soltanto a mostrare l'interessante esempio del cosiddetto assioma di separazione  T1 , o di Fréchet (laddove quello di Hausdorff lo si indica come assioma  T2 ), il quale richiede che:

T1 - Comunque dati due punti distinti  p  e  q  dello spazio topologico  (X, AX) , esistono un intorno  U(p)  di  p che non contiene  q , ed un intorno  U(q)  di  q  che non contiene  p .

[Abbiamo usato per la prima volta qui il tradizionale, in topologia, simbolo "U" per intorno, che sta a ricordare l'iniziale del vocabolo tedesco Umgebung, appunto, in senso geografico: "dintorni".]

   E' chiaro che uno spazio di Hausdorff, come pure si potrà dire uno spazio topologico separato T2 , è sempre uno spazio di Fréchet, mentre il viceversa non è necessariamente vero. Un semplice esempio è fornito da     , ma piuttosto che disperderci in siffatte interminabili casistiche, preferiamo rilevare come gli spazi di Fréchet siano esattamente quelli tali per i quali vale il seguente:

Teorema (11-3-10) -  Uno spazio topologico  (X, AX)  soddisfa all'assioma di separazione  T1  se e soltanto se tutti i suoi punti sono chiusi, o anche se e soltanto se l'intersezione di tutti gli intorni di un qualsiasi punto  x  è uguale al singleton  {x} .

Dim. (Facile).

   Prima di procedere oltre, osserviamo esplicitamente che, ancorché le successioni sono, come sappiamo, delle particolari funzioni, non abbiamo voluto dare, e non daremo, il concetto generale di limite di una funzione qualsiasi  f  definita tra i supporti di due spazi topologici  X  ed  X' (limite da considerarsi in un particolare punto del dominio di  f ), sia perché di tale concetto si occuperanno in modo esauriente i corsi di Analisi (anche nei casi in cui  f  sia definita solamente in un sottoinsieme  Y  di  X , e il punto in cui si voglia considerare il limite non appartenga ad  Y ), sia perché esso non è strettamente indispensabile per i nostri propositi, vale a dire che esso non è necessario se si vuole soltanto definire il concetto di continuità di una funzione (in un punto, o in tutto il proprio dominio). Osserviamo infine che nel caso delle successioni non abbiamo in realtà utilizzato alcuna topologia in  N , anche se l'esempio delle successioni (ove si aggreghi all'insieme  N  un nuovo elemento che si indica usualmente con il simbolo  +¥ , e si definisca un'opportuna topologia nell'insieme risultante da tale estensione) potrebbe invero essere riguardato come un caso particolare di una teoria alla quale, come detto, non faremo neppure fugace cenno. Anche perché per tale via, vale a dire sostanzialmente attraverso il grafico della successione, si sarebbe costretti a visualizzare la teoria dei limiti di successioni in un modo che ci appare irrimediabilmente statico, laddove al contrario, in conformità con la convinzione dell'esistenza di un'analogia profonda tra aritmetica (ordinaria) e tempo, invitiamo piuttosto a concepire le successioni in un modo dinamico, immaginando un punto (o più punti, qualora si introducano delle sottosuccessioni) che si muove nell'appropriato ambiente verso la sua eventuale mèta.

   Torniamo adesso al problema della definizione della categoria    , che, come sempre quando ci si trova di fronte a un nuovo concetto matematico generale, dobbiamo considerare un compito primario.

   Gli oggetti della nostra nuova categoria, Ob() , saranno ovviamente tutti gli spazi topologici, il problema è adesso "decidere" quali morfismi dobbiamo scegliere a costituire  M() , soddisfacendo comunque alle note prescrizioni, e pervenendo a una definizione di isomorfismo topologico (che viene detto usualmente, con una sola parola, omeomorfismo) che corrisponda a quella "naturale". Essendo qualitativamente, come ci si può attendere, un morfismo topologico  j  costituito dalla solita terna ordinata  ((X, AX), (X', AX'), f) , dove i primi due elementi di  j  sono i due spazi topologici rispettivamente dominio e codominio del morfismo, ed  f  una funzione ordinaria tra i rispettivi supporti
( f Î (X,X') = H(X,X') , soddisfacente certe condizioni da determinare), un isomorfismo dovrà essere semplicemente tale che le due famiglie di aperti  AX  e  AX'  si corrispondano biunivocamente tramite  f .

   Orbene, i morfismi topologici vengono identificati con le cosiddette funzioni continue, vale a dire quelle funzioni  f  tra  X  e  X'  che soddisfano intuitivamente al criterio che, dato comunque un punto  x0 Î X , punti "vicini" ad  x0  si trasformano mediante  f  in punti vicini ad  f(x0) .

   Tale condizioni si esplicita formalmente nel seguente modo:

(11-3-11) - " x0 Î X , " intorno U(f(x0)) Í Y , $ intorno V(x0) Í X , tale che
f(V(x0)) Í U(f(x0)) .

[Si badi bene all'ordine logico con cui appaiono dominio e codominio del morfismo! Osserviamo poi che se la condizione precedente è soddisfatta soltanto per qualche punto  x0 Î X , allora si dice che la funzione  f  è continua in  x0 ; vale a dire, la continuità è una proprietà puntuale.]

   Naturalmente la definizione è tale che il prodotto (operatorio) di funzioni continue è una funzione continua, le identità sono funzioni continue, sicché non abbiamo problemi con la struttura categoriale che ci interessa. Qui vogliamo piuttosto verificare subito che risulta in effetti soddisfatta la condizione desiderata per gli omeomorfismi, il che è conseguenza immediata della seguente caratterizzazione delle funzioni continue:

Teorema (11-3-12) - Una funzione  f : X ® X'  (tra i supporti dei due soliti dati spazi topologici) è continua se e soltanto se  " A' Î AX' Þ f-1(A') Î AX .

   Omettiamo la facile dimostrazione di tale teorema, preferendo esibire un'altra caratterizzazione delle funzioni continue, in grado di illustrarne il significato profondo.

Teorema (11-3-13) - Ferma restando l'interpretazione dei simboli, se una funzione  f : X ® X'  è continua, allora, comunque dato un punto  x0 Î X , e comunque scelta una successione di punti  x1, x2, ...  in  X  convergente a  x0 , la corrispondente successione tramite  f : f(x1), f(x2), ... converge in  X'  a  f(x0) .

   Omettiamo anche adesso la facile dimostrazione, completando la discussione osservando che il precedente teorema non può essere perfezionato inserendovi un "se e soltanto se" al posto del semplice "se". Perché si possa avere anche il viceversa del teorema (11-3-13), e quindi una nuova caratterizzazione della continuità, è necessaria qualche ulteriore specificazione sullo spazio topologico dominio del morfismo, per esempio la seguente:

(11-3-14) " x0 Î X , $ una successione monotona decrescente di intorni
U1 Ê U2  Ê U3 ... di x0  in  X , tale che l'intersezione di tutti questi intorni è uguale al singleton  {x} , e per ogni intorno  U(x0)  in  X  esiste un indice  k Î N  tale che  U(x0) Ê Uk .

[Alla seconda proprietà enunciata in (11-3-14) si fa riferimento dicendo che la successione in parola è un sistema fondamentale di intorni di  x0 , mentre la prima, data la seconda, ci garantisce che lo spazio topologico in questione è uno spazio separato alla Fréchet, giusta il teorema (11-3-10). La proprietà (11-3-14) è certamente soddisfatta nel caso della topologia della retta ordinaria (lo studente comprenderà subito la dipendenza di questa asserzione dal Postulato di Archimede: basta prendere un qualsiasi segmento astratto  s Î S , prendere un suo rappresentante centrato in  x0 , poi considerare  s , etc.), del piano ordinario, etc., e in generale di tutti quegli spazi topologici che si dicono metrici, un concetto che verrà introdotto in corsi di livello superiore a quello presente. Osserviamo qui soltanto che tali spazi, nei quali si definisce un'opportuna nozione di distanza, "ereditano" peraltro in qualche senso le loro proprietà topologiche da quelle delle strutture geometriche ordinarie, che abbiamo posto a base della matematica.]

   Concludiamo questo lungo excursus provando che in effetti sussiste il seguente:

Teorema (11-3-15) - Ferma restando l'interpretazione dei simboli, nel caso si abbia a che fare con un spazio topologico  (X, AX)  soddisfacente alla condizione (11-3-15), allora una funzione  f : X ® X'  risulta certamente continua qualora essa sia tale che, comunque dato un punto  x0 Î X , e comunque scelta una successione di punti  x1, x2, ...  in  X  convergente a  x0 , la corrispondente successione tramite  f : f(x1), f(x2), ... converge in  X'  a  f(x0) .

Dim. Supponiamo per assurdo che  f  non sia continua in x0 , e quindi che esista un intorno  U(f(x0))  in  X'  tale che, comunque si prenda un intorno  V(x0)  in
X , la di lui immagine  f(V(x0))  non sia per intero contenuta in  U(f(x0)) . Ciò implica in particolare che, preso l'intorno  U1  di  x0  di cui alla (11-3-15), esisterà un punto  x1 Î U1  tale che  f(x1) Ï  U(f(x0)) , e poi che esisterà un punto x2 Î U2  tale che  f(x2) Ï  U(f(x0)), etc.. Così procedendo, in forza delle proprietà degli enti in gioco, si determina una successione di punti  x1, x2, ...  in  X  convergente a  x0 , ma tale che la corrispondente successione tramite  f : f(x1), f(x2), ... non converge in  X'  a  f(x0) , perché tutti i suoi elementi sono fuori di U(f(x0)) , e la conclusione assurda prova il teorema.

 

11-4 - Continuità e connessione

Introduciamo in questo paragrafo l'annunciata nuova formulazione di PC, in termini squisitamente topologici (statici).

   Premettiamo qualche altra più avanzata nozione di topologia. Abbiamo visto che in ogni spazio topologico  (X, AX)  sia il sottoinsieme vuoto che l'intero  X  sono al tempo stesso tanto aperti quanto chiusi. Orbene, uno spazio topologico tale che questi siano gli unici due insiemi aperti-chiusi si dice connesso. Tale proprietà si enuncia anche dicendo che è impossibile trovare in  X  due sottoinsiemi aperti  A, A' , non vuoti e disgiunti, tali che  X = A È A' . In uno spazio sconnesso, invece, tali spezzamenti possono darsi ( {A,A'} risulta in effetti una bipartizione di  X ), e si dicono appunto sconnessioni dello spazio topologico in oggetto.

   Ciò detto, il postulato di continuità può enunciarsi anche nel seguente modo:

PC5 - La retta ordinaria è uno spazio topologico connesso.

[La dimostrazione che segue mostrerà che risultano connessi, nella topologia indotta per relativizzazione, anche gli intervalli di  R - rispetto a un verso fissato - di qualsiasi specie, chiusi, aperti, etc., e così pure tutte le semirette, sia chiuse che aperte. I sottoinsiemi chiusi e connessi della retta ordinaria si dicono i suoi continui, mentre i suoi sottoinsiemi aperti e connessi si dicono i suoi campi (assistiamo così all'utilizzazione del medesimo termine in un ulteriore contesto semantico, oltre ai "campi" dell'algebra, di cui diremo più avanti in questo libro, e ai "campi di forze" della fisica). In generale, un altro teorema, a questo punto non difficile, identifica i sottoinsiemi connessi di  R  con i suoi sottoinsiemi convessi, ovvero con quei sottoinsiemi  A Í R  tali che, " p, q Î A , il segmento    è interamente contenuto in  A . Ovviamente, una tale caratterizzazione cessa di essere valida nel piano o nello spazio ordinari.]

Dim. Per provare che PC5 è equivalente a uno degli enunciati precedenti di PC, dimostriamo prima di tutto che dal postulato di continuità si deduce che la topologia naturale della retta ordinaria la rende uno spazio topologico connesso. Procedendo per assurdo, sia invero  R = A È A'  una sconnessione di  R , e siano  a , a' due punti scelti ad arbitrio rispettivamente in  A  e in  A' (che sono per ipotesi non vuoti). Poiché  A  e  A'  sono anche supposti disgiunti, a  e  a'  saranno certamente distinti, sicché, fissato per comodità il verso della retta in cui  a'  segue  a , possiamo considerare il segmento    , e in esso il sottoinsieme  A* =  Ç A . Ora  A* , essendo l'intersezione di due chiusi di  R , sarà anch'esso un chiuso di  R . Inoltre, essendo superiormente limitato, avrà un estremo superiore, diciamolo  m , il quale sarà senz'altro un elemento di  A* , in virtù del fatto che detto sottoinsieme è appunto chiuso. Per lo stesso motivo  m  non può coincidere con  a' , il quale si trova in A'* =  Ç A'  che è disgiunto da  A* , e pure tutto l'intervallo semi-aperto inferiormente  ]m,a']  dovrà trovarsi in  A'*  (i punti maggiori di  m  che appartengono al segmento dato non possono stare in  A* , e quindi neanche in  A ). Del resto, in virtù dell'ipotesi ammessa, anche  A'*  è un chiuso di  R , sicché deve contenere tutti i propri punti di aderenza, tra i quali  m , e tale punto verrebbe così ad essere a comune tanto ad  A*  quanto ad  A'* , ovvero tanto ad  A  quanto  ad  A' , contro l'ipotesi di disgiunzione di questi due insiemi.
Dimostriamo viceversa che, noto che la retta  R  è connessa, allora da questa proprietà segue PC, per esempio nella forma PC1. Consideriamo in effetti un sottoinsieme  X Ì R  non vuoto e superiormente limitato rispetto a un verso della retta (fissato al solito in modo arbitrario), e supponiamo per assurdo che  X  non ammetta estremo superiore, ovvero che l'insieme  M  dei maggioranti di  X  non abbia minimo. Tale asserzione implica intanto manifestamente che  M  è un insieme aperto (oltre che non vuoto) di  R , disgiunto da  X . Consideriamo quindi, per ogni punto  x Î X , la semiretta inferiore chiusa di vertice  x , diciamola  S(x) , e facciamo l'unione di tutte queste semirette  S(x)  al variare di  x Î X . Otteniamo in questo modo un sottoinsieme  M' , e l'assurdo sarà provato quando avremo constatato facilmente che: uno, M'  non è vuoto; due, M'  è disgiunto da  M ; tre, M'  è aperto in  R (ogni punto  m' Î M'  appartiene per costruzione a qualche semiretta  S(x) , e se  m' < x  è ovvio che  M'  è intorno di  m' , mentre se  m' = x  la circostanza risulta pure vera, in quanto  x  non può per ipotesi essere un massimo di  X , e quindi esiste sicuramente un  x' Î X  tale che  x < x' ); quattro,  R = M È M' (perché se un punto  p  non è un maggiorante di  X , ovvero non sta in  M , allora esisterà necessariamente un punto  x Î X  tale che risulti  p £ x , ovvero p Î S(x) ), qed.

   Concludiamo questa sezione dedicata allo studio della connessione provando un importante teorema (che verrà opportunamente generalizzato nei corsi di Analisi, con il nome di Teorema di Weierstrass), capace di dare un'idea del ruolo che può svolgere la connessione in determinate questioni.

Teorema (11-4-1) - Considerati due punti distinti  a , b  sulla retta ordinaria  R , e fissato per esempio su  R  il verso in cui  b  segue  a , sia  f : [a,b] ® R  una funzione continua monotona crescente in senso stretto. Allora, ogni punto  p'  in  R  compreso strettamente tra  f(a)  ed  f(b) , f(a) < p' < f(b) , è immagine tramite  f  di uno ed un sol punto  p  compreso strettamente tra  a  e  b , a < p < b . Come dire, l'immagine dell'intervallo  [a,b]  coincide esattamente con l'intervallo [f(a),f(b)] .

Dim. Consideriamo i due sottoinsiemi aperti di [f(a),f(b)] (nella topologia indotta per relativizzazione): A' = [f(a),p'[ , A'' = ]p',f(b)] . Poiché  f  è continua, in virtù del teorema (11-3-12) i due sottoinsiemi  f-1(A')  ed  f-1(A'')  di  [a,b]  risulteranno pur essi aperti in  [a,b]  (e ancora nella topologia indotta per relativizzazione). Se non esistesse alcun punto  p Î [a,b]  tale che  f(p) = p' , allora saremmo evidentemente in presenza di una sconnessione di  [a,b] , e l'assurdo prova l'asserto.

 

11-4 - Il criterio di convergenza di Cauchy

Discuteremo invece in questo paragrafo un'ulteriore formulazione di PC, questa volta in termini, come ci piace dire, dinamici.

   Premettiamo allo scopo la seguente definizione. Una successione

p1, p2, p3, ...

di punti di  R  la si dice una successione di Cauchy, se tutti i suoi elementi sono, da un certo punto in poi, arbitrariamente vicini, ovvero, formalizzando tale concezione intuitiva così come si è fatto a proposito di classi contigue, quando la successione soddisfa alla seguente proprietà:

C -  " segmento libero  s Î S , esiste un indice  ks Î N  (variabile in generale con la scelta di  s ) tale che, comunque presi due numeri naturali  k , k' ³ ks , tali che  pk ¹ pk' , risulta  pkpk' < s . Se si sceglie in particolare una coppia di indici
k ³ ks , ks , si trova che tutti i corrispondenti punti  pk  risultano allora interni a quel rappresentante  s  di  2s  centrato nel punto corrispondente all'indice ks . Ne consegue che, eliminando il fattore  2  sostanzialmente superfluo (basterebbe partire all'inizio da    anziché da  s ) la proprietà in parola si può anche esprimere richiedendo che, comunque fissato un segmento libero  s Î S , esiste un indice  ks Î N  (variabile in generale con la scelta di  s ) tale che tutti i segmenti    (resta sottinteso che essi si prendono in considerazione soltanto nel caso  pk ¹ pk' ) appartengono, dall'indice  ks  in poi, all'interno di in un unico rappresentante  s  di  s ,  Ì s .

   Data la precedente definizione, sussiste allora il seguente:

Teorema (11-4-1) - Una successione convergente soddisfa necessariamente alla condizione C.

Dim. (Facile, e indipendente da PC).

   Il precedente asserto ammette anche una formulazione inversa, la qual circostanza consente appunto l'annunciata nuova enunciazione di PC:

PC6 - Ogni successione di Cauchy della retta è convergente, ovvero, successioni di Cauchy e successioni convergenti costituiscono la medesima totalità, ancorché a priori le prime siano più delle seconde.

Dim. Sarà sufficiente provare per esempio che, ammesso PC6, si può dimostrare PC1, e viceversa. Sia dunque, fermo restando il significato dei termini,  A  un sottoinsieme di punti di  R  non vuoto e superiormente limitato. Nostro intento è dimostrare che  A  ammette un estremo superiore, alla cui esistenza perverremo al seguente modo. Si scelgano un maggiorante qualsiasi  m1  di  A  e un elemento  a1  qualsiasi di  A . Se  a1 = m1  siamo a posto, abbiamo già l'estremo superiore ricercato, supponiamo dunque che risulti invece  a1 < m1 . Si consideri in tale caso il centro  c1  di   . Se  c1  risulta un maggiorante di  A , poniamo
a2 = a1 , m2 = c1 . Se  c1  non risulta un maggiorante di  A , ciò implica che esiste un punto  a2 Î A  con  c1 < a2  , e poniamo in questo caso  m2 = m1 . Se  a2 = m2  siamo ancora una volta a posto, se no abbiamo a che fare, in entrambe le eventualità, con un segmento libero  s2 = a2m2  minore o uguale di  1 , avendo detto  s1  il segmento libero corrispondente al segmento iniziale   . Ripetiamo adesso la costruzione precedente a partire da  a2 , m2 , fino ad ottenere due punti  a3 , m3  tali che o coincidono, ed abbiamo trovato allora l'estremo superiore che ci interessa, oppure tali che  s3 = a3m3 £ 1 , etc.. E' chiaro che, così procedendo, se mai un elemento  ak  viene a coincidere con il corrispondente  mk , riusciremo a costruire due successioni, una di maggioranti di  A , l'altra di elementi di  A , diciamole rispettivamente

m1 ³ m2 ³ m3 ³ ...

e

a1 £ a2 £ a3 £ ... ,

(in effetti:  a1 £ a2 £ a3 £  ...  £ m3 £ m2 £ m1)

la prima delle quali sarà monotona decrescente (in senso lato), e la seconda monotona crescente (in senso lato), tali però che i punti  ak , mk  (nelle attuali assunzioni, sempre distinti tra di loro,  ak ¹ mk ), risultino "indefinitamente vicini" al divergere dell'indice  k  (ancora una volta, ecco qui intervenire il Postulato di Archimede!). E' manifesto che, per costruzione, entrambe le successioni risultano successioni di Cauchy, e allora entrambe, in virtù di PC6, sono convergenti. Diciamo  m  il limite della prima successione, e  a  quello della seconda. Il fatto che i termini delle due successioni siano indefinitamente vicini implica subito che  a = m , e poiché il limite  m  deve "ereditare" dalla successione  m1, m2, ...  la proprietà di essere un maggiorante di  A  (se esistesse un elemento  a Î A  con  m < a , allora tutti gli elementi della successione  m1 , m2 , m3 ... necessariamente presenti da un certo punto in poi in  [m,a[  non potrebbero essere maggioranti di  A , perché in particolare minori di  a - è pure chiaro, in virtù dell'assioma di separazione, che gli elementi  mk  non potranno mai, per alcuna scelta dell'indice  k , essere minori di  m ), ecco che avremo finalmente determinato un maggiorante di  A  che risulta anche un elemento di  A , e quindi addirittura un massimo di A, il che conclude la prima metà della dimostrazione.
Per concludere dobbiamo ancora provare che, inversamente, dato PC, una successione  f  di Cauchy di  R  è necessariamente convergente. In effetti, è chiaro innanzitutto che  f  è limitata (dall'indice  ks  in poi, direttamente in forza della condizione C, mentre i primi  ks-1  elementi di  f , che potrebbero eventualmente essere fuori dal segmento che contiene tutti i successivi, sono soltanto un numero finito, sicché è possibile comprendere l'intera immagine di  f  in un unico segmento). In virtù di tale peculiarità, alla successione possiamo applicare le considerazioni di cui al teorema (11-2-3), in particolare introdurre i due punti  a = minlim(f) £ b = maxlim(f) . E' palese che, poiché alcuni punti di  f  si addensano su  a , mentre altri si addensano su  b , i primi dovendo comunque restare indefinitamente vicini ai secondi, deve risultare  a = b  (se fosse  a < b , i due punti in parola potrebbero essere separati mediante due intorni disgiunti), ovvero  a = b = lim(f) , qed.

 

11-5 - La non numerabilità della retta ordinaria

Siamo ora finalmente in grado (in effetti, lo eravamo già da un pezzo) di tornare alla domanda che avevamo posto all'origine del presente capitolo, e cioè: quanti sono i punti di  R  ? Specificheremo il Teorema 11-1-2 dimostrando che:

Teorema (11-5-1) -       >  !0  ,

ovvero, che  R  non può essere concepita come un insieme numerabile. Rimandiamo al successivo capitolo sui numeri reali la dimostrazione del fatto che risulta invero   =  2! - per tale motivo  2!  si dice la potenza del continuo - provata la quale identità il Teorema (11-5-1) non è altro che una diretta conseguenza del II Teorema di Cantor.

Dim. Ma veniamo a una dimostrazione dell'asserto che ci interessa, dimostrando in particolare che l'interno di un qualsiasi segmento    è esso stesso non numerabile. Fissiamo, ancora una volta per comodità, il verso di  R  in cui  b  segue  a , e consideriamo, una qualsiasi successione di punti distinti

p1, p2, p3, ...

tale che essi siano tutti compresi all'interno del segmento prescelto (ovvero, tali che,  " i Î N ,  a < pi < b ). Considerato il segmento   , dividiamolo in tre parti uguali (tricotomia), introducendo allo scopo due punti q1 , q2  tali che:
p1 < q1 < q2 < b , e   =  =  . Guardiamo adesso al punto  p2  e al segmento   . Se  p2  non è interno a tale segmento, si introducano i punti r1, r2 , interni ad esso, tali che il segmento    corrisponda alla terza parte (quella "centrale") di   , e si proceda oltre a considerare  p3  in relazione a   . Se invece  p2  è interno a   , si ripeta la tricotomia di cui al primo passo con riguardo al segmento   .

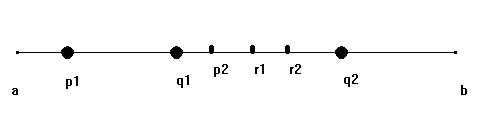
Fig. 11-5-2

   E' chiaro che, così procedendo, si determina una successione monotona decrescente (in senso stretto) di segmenti

 É  É   ...

tale che un punto ad essa comune, certo esistente in virtù di PC3, non può coincidere, per costruzione!, con nessuno dei punti della successione di partenza, qed.

[E' forse opportuno osservare che l'interno di un segmento ha lo stesso numero cardinale dell'intera retta, come mostra per esempio la corrispondenza biunivoca  p ® p'  che viene illustrata nella seguente figura:

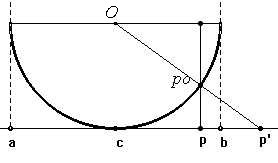
Fig. 11-5-3

   Per il centro  c  di    si lascia passare la semicirconferenza tangente  C , di centro  O , riportata in figura, inscritta al quadrato di lato   ; poi, dato un qualsiasi punto  p  all'interno del segmento, si determina il punto  p0  su  C  , situato sulla medesima verticale di  p , e infine si costruisce  p' Î R  come illustrato.
Osserviamo infine che hanno lo stesso numero cardinale, in forza dei noti teoremi sui cardinali infiniti, tutte le semirette e tutti i segmenti di  R , sia aperti che chiusi, etc.. Il "teorema dell'infinito" mostra anche che il piano ordinario, e lo spazio ordinario, hanno lo stesso numero cardinale della retta ordinaria, così come un cerchio, l'interno di un cerchio, etc., e pertanto tutti questi insiemi sono essi pure non numerabili.]