Teoria degli insiemi e delle funzioni

 

Parte I - Insiemi

Prendiamo le mosse, nel nostro itinerario alla ricerca del contenuto della matematica, dai concetti generali, e sostanzialmente "primitivi", di INSIEME e di FUNZIONE, movendoci così su un terreno che potrebbe ancora dirsi aspecifico della nostra particolare disciplina, in quanto comune a ogni scienza che voglia pervenire a una sistemazione concettuale dei fenomeni di sua competenza. Tenendo conto della puntualizzazione kantiana riportata nell'Introduzione, non sarebbe errato ritenere di stare compiendo alcune investigazioni nell'ambito della logica generale.

Concretizziamo tale proposito analizzando avanti tutto la capacità dell'intelletto puramente "logica" di considerare, e quindi trattare, collettività di enti come un unico nuovo ente. Ecco la definizione cantoriana di insieme: [Georg Cantor fu il primo ad occuparsi sistematicamente, dal 1874 in poi, di teoria degli insiemi; andrebbe sottolineato con cura il dettaglio che proprio uno dei settori della matematica ultimo arrivato venga viceversa oggi comunemente accettato quale punto di partenza su cui costruire gradualmente ("fondare") l'intero complesso edificio della matematica.]

<<Per insieme si intende un raggruppamento in un tutto di oggetti ben distinti della nostra intuizione o del nostro pensiero>>.

(I-1) Nota. In quell'aggettivo <<distinti>> presumiamo avvertire echi di cartesianesimo, come pure nel termine <<nostra intuizione>>, che fa implicito riferimento a quelle che potrebbero dirsi le modalità con cui si "struttura" il pensiero umano (una prospettiva antropocentrica sgradevole a certe orecchie postdarwiniste). <<Vi sono anche delle persone che, in tutta la loro vita, non percepiscono nulla come è necessario per bene giudicarne. Poiché la conoscenza sulla quale si può stabilire un giudizio indubbio dev'essere non solo chiara, ma anche distinta. Io chiamo chiara quella che è presente e manifesta [...] ad uno spirito attento [...] E distinta, quella che è talmente precisa e differente da tutte le altre, da non comprendere in sé se non ciò che appare manifestamente a chi la considera come si deve. [...] la conoscenza può essere chiara senza essere distinta, ma non può essere distinta senza essere in pari tempo chiara>> (dai principi NN. 45 e 46, Parte I dei Principia Philosophiae di Cartesio, 1644). <<E' certo che noi non prenderemo mai il falso per vero, fino a che non giudicheremo se non di ciò che percepiamo chiaramente e distintamente>> (dal principio N. 43, Parte I dei Principia...). L'esortazione agli studenti di matematica principianti è di non accettare mai per scontato nulla che non sia chiaro e distinto, secondo la loro esperienza e coscienza.

Gli <<oggetti>> da cui è costituito un insieme si dicono i suoi elementi. Il termine "insieme" ammette diversi sinonimi, che noi cercheremo usualmente di evitare, [Sebbene non sempre, concedendo qualcosa al fenomeno linguistico della ridondanza, che può avere ricadute benefiche sia sul piano estetico, sia su quello "psicologico", a tener desta cioè l'attenzione. Si potrebbe ritenere infatti che un'esposizione troppo "coerente", cioè automatica simil "macchina", potrebbe essere controproducente da un punto di vista didattico, indurre cioè un aumento del livello di sonnolenza da parte del discente.] preferendo riservare a qualcuno di essi un significato più specifico. Essi sono: collezione, collettività, aggregato, totalità, gruppo, classe, famiglia, etc. (è preferibile evitare l'uso degli ultimi tre in particolare).

Dicevamo che quello d'insieme va inteso come un concetto sostanzialmente primitivo, perché non si sente il bisogno (né si sentì nel primo momento della sua introduzione) di dare una "definizione" del concetto di insieme che si poggi a sua volta su altri concetti ad esso preliminari. Soprattutto, non si sente il bisogno di darne una definizione formale ("assiomatica"), mediante un'elencazione delle proprietà di cui godono gli insiemi, osservazione questa che si capirà meglio nel seguito quando da definizioni formali saremo (talora giustamente) sommersi. Citiamo ancora Cartesio: <<vi sono delle nozioni di per se stesse così chiare, che le si oscura volendole definire alla maniera della scuola, e che non s'acquistano con lo studio, ma nascono con noi>> (principio N. 10, Parte I dei Principia...).

Spendiamo appena qualche parola sulla "questione di senso": come si dà un insieme? (ad altri o a noi stessi!), una risposta alla quale domanda deve considerarsi comunque già implicitamente fornita nella definizione cantoriana di insieme, e nella successiva nota (I.1). Un insieme A può considerarsi "dato" quando sia assegnato un "criterio" che permetta di individuare univocamente tutti e soli gli elementi dell'insieme, e vedremo come tale concetto si preciserà (o si estenderà) mano a mano che si acquisterà maggiore dimestichezza con i procedimenti usuali della matematica. E' opportuno però aggiungere sin da ora che si incontreranno sostanzialmente due tipi di "definizione" di un insieme, una più "comune", e una più "rara". Quella che si incontra più frequente consiste nell'individuazione di un'espressione linguistica, o proposizione (costruita mediante le regole del "linguaggio", più o meno formale, che si utilizza), la quale specifichi le proprietà caratterizzanti gli elementi dell'insieme che si vuole definire. Una simile definizione può dirsi sintetica, implicita, nominale (l'importante è comprendersi), o anche, come preferiremo, intensiva, termine che fa riferimento al concetto di "concentrato". Un esempio di definizione intensiva dell'insieme A dei numeri primi naturali non superiori a 20 (per il momento basterà ricordare che si dicono naturali i numeri {1, 2, 3,...}, e che alla loro totalità - infinita - si fa consueto riferimento con il simbolo N; sottolineiamo subito la circostanza che per definire un insieme si usano generalmente delle parentesi graffe) è quella che pone:
A = {x Î N tali che 1 < x £ 20 e x non ha divisori diversi da se stesso e dall'unità} (è usuale non considerare 1 come un numero primo). Per contro, una definizione estensiva dello stesso insieme (estensiva come contrario di intensiva, ma vanno anche bene: esplicita, palese, o, come preferiremo, ostensiva, con chiaro significato del termine - si pensi all'ostensorio nelle chiese cattoliche) è semplicemente la seguente: A = {2, 3, 5, 7, 11, 13, 17, 19}. Si noti che la precedente definizione dell'insieme infinito N era anch'essa ostensiva, e che il simbolo dei tre puntini "..." stava a significare semplicemente che l'interlocutore concepiva benissimo nel suo intelletto cosa dovesse esserci al posto dei puntini. E' ovvio che il primo tipo di definizione ci informa sul criterio con cui A deve concepirsi, ma non di renderci (almeno immediatamente) edotti su quanti e quali siano i suoi elementi. Per esempio, facendo riferimento a un celebre secolare (e tuttora irrisolto) problema di "teoria dei numeri", potremo senz'altro distintamente concepire quello che possiamo denominare l'insieme G dei "numeri di Goldbach", ovvero l'insieme di quei numeri naturali pari che non siano somma di due numeri primi dispari, ma non sapremmo dire se G contiene qualche altro elemento oltre agli ovvi 2 e 4 (sapremmo dire per esempio che G non contiene 6 = 3+3, non contiene 8 = 3+5, non contiene 10 = 5+5 = 3+7, etc.), dal momento che proprio una congettura di Goldbach ipotizza che ogni numero pari superiore a 4 sia sempre somma di due numeri primi dispari. Con il secondo tipo di definizione (che comincia ovviamente a incontrare qualche difficoltà nel caso di insiemi con infiniti elementi) sappiamo invece subito esattamente come è fatto l'insieme di cui trattasi, mentre rischia peraltro di sfuggirci la proprietà "collettivizzante" con cui esso è stato pensato. Si tenga comunque costantemente conto che stiamo parlando di enti del pensiero, e che, laddove la concezione che abbiamo di un qualche ente può (deve) essere chiara e distinta, ci troveremo spesso di fronte al fenomeno dell'inadeguatezza del linguaggio (soprattutto nel caso di enti "infiniti"): <<le language est source de malentendus>> (il linguaggio è all'origine di fraintendimenti), come si osserva in Le petit prince di Antoine de Saint-Exupéry. Però il pensato non va confuso con il parlato, ed anche se l'aspetto comunicativo-formale della matematica è quello più appariscente, è manifesto che essa, quanto a significato-contenuto, appartiene tutta al regno del pensato. Comunque, ci accontenteremo che sia chiara e distinta la procedura di costruzione dell'insieme A, o la specificazione dei suoi oggetti, o anche solo la semplice "esistenza" di A nella nostra mente, in base a certe sue proprietà che ci sembra possano essere sufficienti allo scopo (vedremo nel seguito per esempio l'uso che si fa in questo senso del cosiddetto assioma della scelta). L'idea di fondo è che esistono certi "oggetti" a loro volta primitivi in una sorta di universo (potenziale e indeterminato), e che di essi si possano considerare talune collettività di prima generazione, le quali vanno ad aumentare il numero degli oggetti dell'universo (che va quindi concepito come una "entità" in espansione), sicché insiemi di seconda generazione possono essere costituiti tanto da oggetti primitivi quanto da insiemi di prima generazione. [Per evitare alcuni noti "paradossi di fondazione", ai quali qua e là accenneremo, si eviti di considerare lo stesso universo U come un oggetto primitivo, sicché U non è elemento di se stesso. Se si vuol costruire un insieme di prima generazione che contenga tutti gli oggetti primitivi, lo si chiami pure per esempio U, ma con questa operazione l'universo deve ritenersi "cresciuto"; ovvero, abbiamo adesso un "secondo" universo, denotiamolo U2, che contiene quel "primo" universo U, che allora potrebbe essere denotato con il simbolo U1, etc..] Quale esempio, prendiamo come oggetti primitivi i simboli numerici 1, 2 e 3, e consideriamo gli insiemi di prima generazione:
I = {1, 2}, J = {1, 2, 3}. Possiamo poi senz'altro concepire l'insieme di seconda generazione: A = {1, 2, 3, I} = {1, 2, 3, {1, 2, 3}} (attenzione alle parentesi graffe ripetute!), e così via. Un importante caso particolare di tale procedura è di costruire, a partire da un qualsiasi insieme A, un nuovo insieme {A}, definito come quell'insieme il cui unico elemento sia l'insieme A (quando si è di fronte a un insieme con un unico elemento, si dice che esso è un singleton; nel caso in considerazione si parla allora del singleton di A). Per esempio, possiamo introdurre il singleton di J: {J} = {{1, 2, 3}}.

E' conveniente cominciare a introdurre presto delle scritture simboliche (semplice utile stenografia) per esprimere certe asserzioni.

a Î A si legge: l'oggetto a, di qualsiasi natura esso possa essere, è un elemento dell'insieme A (in ciò che precede si è implicitamente introdotta la convenzione di usare lettere latine maiuscole per gli insiemi, mentre lettere latine minuscole indicheranno di solito gli elementi di un insieme; poiché un insieme può a sua volta essere costituito da insiemi, tale convenzione è però destinata spesso a cadere). Il simbolo Î si dice il simbolo di Peano (dal nome del matematico torinese Giuseppe Peano), o simbolo di appartenenza. Come esempio, notiamo che la scrittura A Î {A} è allora corretta, mentre la scrittura A Î A "di solito" non lo è, per esempio se A è l'insieme {1, 2, 3, I} di cui sopra. Può in tal caso scriversi correttamente A Ï A, una barra trasversale apposta su un simbolo significando la sua negazione.

(I.2) Nota. Nelle righe precedenti si è toccata di sfuggita una questione che ha dato origine a un celebre "paradosso" della teoria degli insiemi (Bertrand Russell, 1902). A tali problematiche daremo un cenno in uno dei capitoli successivi dei presenti Elementi..., ma possiamo dire sin d'ora che, lasciandoci guidare dal criterio delle idee "chiare e distinte", è legittimo concepire un insieme A quando siano stati assegnati in precedenza certi oggetti che andranno a costituire A, il quale "nasce" quindi soltanto dopo quegli oggetti, e non può coincidere pertanto con uno di essi. Come dire che, per ogni insieme A correttamente individuato, non può essere mai A Î A (su un altro simile "rompicapo" logico spenderemo qualche parola tra poco).

Si introducono speciali notazioni simboliche pure per indicare la circostanza che un insieme A sia sottoinsieme di un altro insieme B, ovvero che tutti gli elementi di A siano anche elementi dell'insieme B: A Í B. La barra orizzontale sta a prevedere, come nel caso dei noti simboli di disuguaglianza numerica, minore o uguale £ e maggiore o uguale ³, che i due insiemi in parola possono al limite essere uguali. Si usa invece il simbolo: A Ì B quando si vuole specificare la circostanza che: A Í B e A ¹ B, e si parla in questo caso di un'inclusione propria, o "in senso stretto" (si sottolinea a parole il fatto che una certa inclusione non è, o potrebbe eventualmente non essere, propria, dicendo che essa è impropria, o "in senso lato"). Si osservi che, come è usuale per i predetti simboli di disuguaglianza, tutte le precedenti "relazioni" possono essere scritte anche in senso inverso: A ' a, B Ê A, B É A. Si osservi inoltre, per esempio, che in ordine al singleton {A}, non è vero né che sia {A} Í A (se così fosse, poiché A Î {A}, ne potremmo dedurre A Î A, che abbiamo giudicato assurda nella nota (II.2)), né che sia A Í {A}, tranne un caso particolare che andremo a illustrare (in (I.3)) dopo aver introdotto un nuovo importante concetto.

Tra i sottoinsiemi di un dato insieme A conviene considerare il cosiddetto insieme vuoto, che si designa con il simbolo Æ, e deve ritenersi come quell'unico insieme che è assolutamente privo di elementi, e che in quanto tale deve allora considerarsi come sottoinsieme di ogni insieme. Di conseguenza sono corrette le seguenti scritture: Æ Í A per ogni insieme A, anzi Æ Ì A con inclusione propria, a meno che non sia A stesso l'insieme vuoto, nel qual caso è corretto scrivere Æ Í Æ, ma non è corretto scrivere Æ Ì Æ.

Tanto per rimanere in quest'ambito di considerazioni (che possono a prima vista apparire speciose, ma sono invece assai istruttive e utili), non è corretto scrivere Æ Î Æ, mentre è corretto scrivere sia Æ Î {Æ} sia "ovviamente" Æ Í {Æ}, anzi Æ Ì {Æ}.

L'insieme di tutti i sottoinsiemi di un dato insieme A è un insieme che ricorrerà spesso nelle nostre considerazioni, e si indica con il simbolo P(A), dove la lettera P sta a ricordare che si tratta di "parti" dell'insieme A. Si può scrivere sinteticamente: P(A) = {tutti gli insiemi X ô X Í A}, osservazione che ci consente di introdurre un'altra abbreviazione, una barra verticale ô che si legge "tale (o tali) che" (al posto del simbolo "½" si può usare il simbolo ":", di cui faremo uso talvolta per evitare ripetizioni ravvicinate della barra verticale; ci sono pure altre convenzioni, che noi però ignoreremo). In P(A) sono compresi naturalmente l'insieme vuoto, l'insieme A stesso, tutti i singleton {a} dei diversi elementi di A (allorché A non sia vuoto!), sicché tutte le seguenti asserzioni sono corrette:

X Í A è la stessa cosa che X Î P(A) ; Æ Î P(A) ; A Î P(A) ; per ogni elemento di a, {a} Î P(A).

(Si noti che stiamo in qualche senso introducendo delle regole generative che permettono di asserire l'esistenza nel nostro "universo" di certi enti una volta che ne siano dati degli altri, per esempio il singleton di un insieme A o di un oggetto x una volta che siano dati A o x, l'insieme delle parti P(A) di ogni dato insieme A, etc., oltre a delle vere e proprie asserzioni contenutistiche di esistenza: nell'universo ci deve essere almeno un insieme vuoto Æ, privo cioè di elementi, che risulterà poi anche l'unico insieme privo di elementi, ci devono essere almeno i "numeri" 1, 2, 3,... etc., la scelta è piuttosto "libera".)

Aggiungiamo che risultano entrambe legittime le asserzioni Æ Î P(A) e
Æ Í P(Æ), e che mentre A Î P(A) è pure sempre corretta, invece l'asserzione
A Í P(A) non lo è in generale (vedi (I.3) e (I.7)). Inoltre, che P(A) non è mai vuoto, qualunque sia l'insieme A, compreso il caso A = Æ (l'insieme P(Æ) coincide con il singleton del vuoto, P(Æ) = {Æ}). Infine, che siamo adesso in grado di discutere completamente la possibile inclusione A Í {A}. Da essa si trae infatti: A Î P({A}) = {Æ, {A}}, e quindi abbiamo due casi mutuamente escludentisi: o A = Æ, o A = {A}. La seconda eventualità va certo scartata, perché da essa, e dalla A Î {A}, si dedurrebbe ancora una volta l'assurda
A Î A, mentre la prima eventualità, A = Æ, fornisce l'unico caso in cui risulti di fatto A Í {A}.

(I.3) Piccolo rompicapo. Abbiamo accennato al fatto che è "raro" risulti A Í P(A), una questione che è collegata al caso in cui un elemento a di un insieme A sia anche un sottoinsieme di quell'insieme, cioè si abbia simultaneamente: a Î A e a Í A. Se prendiamo per esempio i seguenti oggetti: i simboli numerici 1, 2 e 3, e l'insieme I = {1, 2}, possiamo senz'altro concepire l'insieme A = {1, 2, 3, I} = {1, 2, 3, {1, 2, 3}} di cui abbiamo già parlato, ed ecco allora che risulta manifestamente sia I Î A, sia I Í A, ovvero I Î A e I Î P(A) (ma non A Í P(A)). Più difficile è capire che esistono insiemi per cui la precedente circostanza sussiste per tutti gli elementi di A (nel caso analizzato essa valeva di fatto solo per l'elemento I, ovvero I era l'unico elemento a comune tra A e P(A)), ovvero tali che A Í P(A). Per avere un siffatto "strano" insieme, basta prendere ad esempio i seguenti oggetti: l'insieme vuoto Æ, e l'insieme K che ha come unico elemento l'insieme vuoto, vale a dire K = {Æ} (singleton del vuoto). Costruito adesso l'insieme con due elementi A = {Æ, K} = {Æ, {Æ}}, ecco che risulta: P(A) = {Æ, {Æ}, {{Æ}}, A}, ed è chiaro che in questo caso vale proprio l'inclusione A Í P(A). Si osservi, per concludere questa nota, che A non può mai essere uguale a P(A) (basta osservare che: A Î P(A), ma A Ï A), e che in quanto precede non avremmo potuto per esempio sostituire all'insieme vuoto il simbolo numerico 1, poiché l'insieme B = {1, {1}} non gode della proprietà richiesta. Infatti, risulta: P(B) = {Æ, {1}, {{1}}, B}, e tutto ciò dimostra quanto il vuoto debba ritenersi un insieme assai speciale. Il problema è che uno stesso insieme vuoto viene inteso come sottoinsieme di qualsiasi insieme (ne consegue che l'intersezione di tutti gli insiemi P(X), ciascuno dei quali è diverso dal vuoto, al variare di X, non è vuota, dovendo contenere l'insieme vuoto!), sicché il vuoto che rappresenta l'insieme dei miliardi nel conto in banca di chi scrive - e assai presumibilmente pure di chi legge - viene inteso come il medesimo vuoto che rappresenta l'insieme delle occorrenze della parola "mxyzptlk" nel prossimo capitolo di questo libro. In effetti, nel caso precedente, a partire dal "simbolo" Æ (passo 1) abbiamo costruito l'insieme A (passo 2), e lo stesso simbolo Æ (passo 3) ha designato il sottoinsieme vuoto di A.

Per affrontare meglio lo studio dei "fenomeni" di nostro interesse, conviene introdurre subito ulteriori simboli, appartenenti a quella che potrebbe dirsi la stenografia della "logica".

Prima di tutto due simboli quantificatori: " che significa "per ogni", ed $ che significa "esiste" (ad esso viene talora aggiunto un punto esclamativo, $!, per esprimere il concetto "esiste ed è unico"). Notiamo che talvolta " può essere letto come un semplice "tutto", o "tutti".

Poi due connettivi logici: Ù che indica la congiunzione "e" (latino et), e Ú che indica la disgiunzione inclusiva "o" (ossia il latino vel, non l'aut che è disgiunzione esclusiva, che si usa quando un'alternativa esclude l'altra).

Un prefisso di negazione, Ø, che collocato davanti a un certo asserto significa che esso è falso.

Esempio: come è possibile esprimere la disgiunzione esclusiva aut con i soli simboli precedenti, ovvero senza introdurne uno nuovo apposito? Dati due asserti p e q, se li si vuole escludere a vicenda, basta scrivere:
p aut q = (pÙØq)Ú(ØpÙq).

Un simbolo di implicazione: Þ . Esso significa che l'asserto che si trova alla sinistra del simbolo implica l'asserto che si trova alla destra del simbolo (c'è chi usa il simbolo ®, che noi preferiamo però riservare al caso delle funzioni, che presto discuteremo). Un modo di intendere l'implicazione p Þ q tra due asserti p e q, è quello di dire che pÙ(Øq) è impossibile.

Qualora due asserti p e q si implichino reciprocamente, si introduce un nuovo simbolo Û, che può essere interpretato come un simbolo di equivalenza logica: anziché scrivere (p Þ q)Ù(q Þ p), si scriverà più brevemente p Û q (quanto detto nella sezione precedente potrebbe allora esprimersi simbolicamente come:
(p Þ q) Û [Ø(pÙ(Øq))]. Notiamo che talvolta Þ può essere letto come un semplice "segue", "allora".

Esercizio: come si nega la congiunzione Ù? Come si nega la congiunzione Ú?

Ø(pÙq) Û [(Øp)Ú(Øq)]

(esempio: (p Þ q) Û [Ø(pÙ(Øq))] Û [(Øp)Ú(Ø(Øq))] Û [(Øp)Úq], poiché Ø(Ø(q)) Û q, due negazioni successive si elidono)

Ø(pÚq) Û [(Øp)Ù(Øq)].

Prima di abbandonare l'ambito puramente logico-descrittivo delle considerazioni precedenti, diamo un cenno a due celebri "modi" di utilizzare un'implicazione, che si dicono rispettivamente del modus ponens e del modus tollens:

(I.4) [(p Þ q)Ùp] Þ q,

(I.5) [(p Þ q)Ù(Øq)] Þ (Øp),

e riportiamo un'altra importante legge dell'inferenza logica generale, molto usata nelle dimostrazioni matematiche, soprattutto quelle "per assurdo". Essa afferma che:

(I.6) (p Þ q) Û (Øq Þ Øp)

In effetti, se ho per esempio (p Þ q), e se avessi anche p, allora per modus ponens sarei sicuro della validità di q, sicché se so pure che q non è vera, ecco allora che non può essere di conseguenza vera p; reciprocamente, se parto da (Øq Þ Øp), allora pÙ(Øq) non può che essere impossibile, perché se avessi un caso in cui p e Øq coesistono, e dal momento che Øq implica p, ecco che avrei anche un caso in cui p e Øp coesistono. La pÙ(Øp) è un'impossibilità logica, mentre la pÚ(Øp) è una tautologia, cioè un'affermazione sempre vera.

(I.7) Nota. L'introduzione dei simboli quantificatori consente di soffermarci un poco sul significato del termine "in generale", che spesso si incontra in matematica. Affermare per esempio che l'inclusione A Í P(A) non sussiste in generale, ovvero che in generale
Ø(A Í P(A)), significa che nella precedente proposizione formalizzata si intende sottintesa una quantificazione della variabile A con il simbolo $, vale a dire che la formalizzazione completa dell'asserzione in oggetto è: [$ A ½ Ø(A Í P(A))]. A parole, si può dire che l'insieme A = {Æ, K} è un esempio di validità della relazione A Í P(A) (o della A Ì P(A)), la quale quindi non è vuota, però non è neppure vera in generale, dal momento che esiste qualche insieme A (A si chiama allora un controesempio alla validità della relazione in causa; nel caso specifico, poi, sono controesempi "quasi tutti" gli insiemi!), per cui si può dire che la relazione in oggetto non sussiste tout court. Possiamo anche provare a rispiegare il tutto attraverso altri concetti, cogliendo l'occasione per effettuare un'analisi più dettagliata di alcuni importanti fenomeni logico-linguistici. Assegnati: (1) un certo insieme A; (2) un certo predicato P(x), [Ora P è iniziale di "predicato", e non di "parte"; purtroppo i simboli dell'alfabeto a nostra disposizione sono pochi, e per questa ragione si utilizzano a volte anche altri alfabeti, senza comunque riuscire a ovviare completamente alla penuria di simboli di fronte alla molteplicità di concetti] che può essere semplicemente inteso come un'asserzione "sensata" per gli elementi di A, la quale per " singolo x Î A possa dirsi inequivocabilmente o vera o falsa (qui la particella "o" funge da aut); allora noi possiamo concepire il sottoinsieme A' Í A costituito da quegli elementi x Î A tali che per essi il predicato P sia vero. In simboli, A' = {x Î A ½ P(x)}. Orbene, l'asserzione di cui trattasi si dirà vera, sottinteso senza eccezioni, in A, se A' = A, cioè se: " x Î A Þ P(x). Si dirà falsa, o non vera in generale, se A' ¹ A, ovvero se:
Ø[" x Î A Þ P(x)], il che equivale a dire: [$ x Î A Þ ØP(x)]. Ma si noti bene che la proposizione p = "P(x) non è vera in A", o anche "P(x) è falsa in A", non va confusa con la proposizione "(ØP(x)) è vera in A", la quale significa invece che [" x Î A Þ ØP(x)] (in p compare un quantificatore $ al posto del precedente quantificatore "). L'identità logica tra le due proposizioni sussisterebbe soltanto nel caso in cui A', oltre ad essere diverso da A, fosse addirittura vuoto, sicché si può concludere che "in generale" abbiamo tre possibilità: A' = A (P(x) è vera in A); A' ¹ A e A' ¹ Æ (P(x) non è vera in A, o è falsa in A, e in A ci sono sia esempi che controesempi del predicato P(x)); A' = Æ ((ØP(x)) è vera in A, ovvero P(x) è vuota in A). Perché abbiamo usato ancora una volta la specificazione "in generale"? Ma perché quanto precede vale a rigore solo se A ha almeno due elementi: infatti, nel caso di un singleton, le tre possibilità si riducono a due (e cosa può dirsi nel caso che A sia l'insieme vuoto? Vero e falso qui diventano la stessa cosa!). Allo studente non mancheranno "infiniti" casi nei quali mettere in pratica la semplice analisi logica che precede (un predicato può essere un'asserzione sull'età dei suoi conoscenti, sul luogo di provenienza dei suoi compagni di studio, etc.). Aggiungiamo piuttosto una riflessione sulla circostanza che, quando nel "linguaggio comune" si dice che una certa proprietà è valida o non è valida in generale, si intende anche specificare che è "raro", infrequente, il caso in cui così non sia, ma questa è una modalità dell'espressione assai più difficile da precisare in un senso matematico esatto. Accenniamo soltanto al fatto che in geometria la precisazione avverrebbe mediante il concetto di dimensione, e che in teoria degli insiemi si potrebbe usare il confronto tra numeri cardinali, che illustreremo nel III capitolo. In generale (un'altra volta, appunto!), è necessario avere una sorta di "misura" dell'insieme dei casi "eccezionali" rispetto a quelli "generali", ma se le eccezioni sono relativamente poche, e sono quindi elencabili, è preferibile per esempio affermare che un certo asserto è vero o non è vero tranne alcuni casi che vengono esplicitamente determinati. Per esempio, abbiamo visto che l'inclusione A Í {A} non è mai vera, per nessun insieme A, tranne nel caso in cui A sia l'insieme vuoto, un'enunciazione questa che è più esauriente della semplice: "A Í {A} non è vera in generale", la quale deve ritenersi comunque corretta.

Si osservi che in quanto precede abbiamo fatto largo uso di parentesi (se si vuole di vario tipo, secondo le convenzioni certamente a tutti note; è però preferibile evitare l'uso delle parentesi graffe, che è meglio riservare, come abbiamo visto, alle "definizioni" degli insiemi). Queste, assieme a possibilmente diversi segni di interpunzione, vengono introdotte per maggiore chiarezza, in un modo che può essere più o meno pedante, a piacere; l'importante è che anche un'esposizione "trasandata" sia capace di tramutarsi, se del caso a richiesta, in una "perfetta".

(I-8) Nota. Andrebbe forse sottolineato il fatto che stiamo considerando anche l'implicazione come un concetto sostanzialmente primitivo, nel senso che riconosciamo al nostro intelletto la facoltà incondizionata di accettare o meno la validità di un'implicazione; ovvero, che lo lasciamo libero di decidere quando un'implicazione tra due termini di un discorso possa essere concepita sussistere in modo chiaro e distinto. Per esempio, può ritenersi abbastanza comprensibile-accettabile la convenzione secondo la quale un'implicazione si considera comunque corretta se la "premessa" è vuota o falsa, qualsiasi sia la "tesi", vuota, vera o falsa. In ogni caso, ribadiamo il suggerimento, tutto va preso cum grano salis, cioè fino a nostra completa e onesta soddisfazione (che è l'unica degna mèta a cui lo spirito di uno studioso deve aspirare).

Diamo qualche esempio di applicazione di tale strumentario in casi semplicissimi.

Esprimiamo l'inclusione tra due insiemi, A Í B:

A Í B Û (" x Î A) Þ (x Î B),

mentre l'identità tra due insiemi, A = B, si esprime ovviamente come:

A = B Û (A Í B)Ù(A Ê B) Û [(" x Î A) Þ (x Î B)]Ù[(" x Î B) Þ (x Î A)].

Esercizio: come si esprime invece l'enunciato che due insiemi A e B sono diversi tra loro, ovvero che: A ¹ B? Bisognerà negare l'ultima delle stringhe precedenti (il termine sta per una sequenza di "segni" di un dato "alfabeto", e avremo occasione di precisarlo e utilizzarlo meglio nel seguito), ovvero scrivere, "semplificandola" un poco:
Ø[[(" x Î A) Þ (x Î B)]Ù[(" x Î B) Þ (x Î A)]].
In base alle regole che già conosciamo, risulterà:
Ø[[(" x Î A) Þ (x Î B)]Ù[(" x Î B) Þ (x Î A)]] Û
Û[Ø[(" x Î A) Þ (x Î B)]]Ú[Ø[(" x Î B) Þ (x Î A)]] Û
Û [($ x Î A) ½ Ø(x Î B)]Ú[($ x Î B) ½ Ø(x Î A)].
Così come l'uguaglianza tra A e B, la disuguaglianza tra A e B si esprime attraverso la congiunzione di due enunciati, diciamoli p e q, nell'ordine, ciascuno dei quali preso separatamente implica detta disuguaglianza, ma non equivale ad essa: (A ¹ B) Û pÚq ; p Þ A ¹ B (ma non: p Û (A ¹ B));
q Þ A ¹ B (ma non: q Û (A ¹ B)); (A = B) Þ Øp; (A = B) Þ Øq. Si può cogliere l'occasione per segnalare in modo esplicito l'ovvia validità generale (ovverosia, per ogni coppia di proposizioni p, q) delle: p Þ pÚq, q Þ pÚq (invero, i due asserti sono la stessa cosa, poiché: pÚq Û qÚp, allo stesso modo:
pÙq Û qÙp; Ø(pÚq) Þ Øp; (Øp)Ù(Øq) Þ Øp; la quale ultima corrisponde manifestamente alla: pÙq Þ p, etc.).

Lo studente si eserciti anche a leggere, o se si preferisce "tradurre", le seguenti asserzioni "compatte":

* (" oggetto x) Þ (x ÏÆ) ; o anche (" oggetto x) Þ Ø(x Î Æ) ;

** (" insieme A) Þ (Æ Î P(A)) ; (" insieme A) Þ (A Î P(A)) ;

*** (" insieme A) Þ (P(A) ¹ Æ) ;

**** (" insieme A) Þ [(P(A) è un singleton) Û (A = Æ)] ;

***** (" coppia di insiemi A, B) Þ [(A Í B) Û (P(A) Í P(B))] ;

****** (" terna di insiemi A, B, C) Þ [(A Í B)Ù(B Í C) Þ (A Í C)]

etc. etc., di simili asserzioni "luminosamente evidenti" ce n'è a iosa.

Quanto precede risulta estremamente comodo per definire e descrivere in modo sintetico le OPERAZIONI naturali tra insiemi.

Unione, per la quale si usa il simbolo È (corrispondente a Ú):

AÈB = {" x ½ (xÎA)Ú(xÎB)}

Intersezione, per la quale si usa il simbolo Ç (corrispondente a Ù):

AÇB = {" x ½ (xÎA)Ù(xÎB)}

Complementazione (corrispondente a Ø):

per ciascun elemento X Î P(A), ovvero per ciascun sottoinsieme X Í P(A), con il simbolo CA(X) si indica il sottoinsieme di A complementare di X (esso si dice il complementare di X in A, la specificazione "in A" venendo di solito omessa quando sia chiaro il riferimento all'ambiente), vale a dire l'insieme di tutti gli elementi a Î A tali che a Ï X. In simboli:

CA(X) = {" a Î A ½ Ø(aÎX)}.

Ovviamente, risulta sempre: A = XÈCA(X), e XÇCA(X) = Æ, la seconda relazione esprimendosi a parole con il dire che X e CA(X) sono disgiunti.

Differenza, per la quale si usa il simbolo "-", ma c'è pure chi usa il simbolo "\":

A-B (oppure A\B) = CA(AÇB) = {" a Î A ½ Ø(a Î B)}

Si noti che, per esempio: " coppia d'insiemi A, B, (A-B = Æ) Û (A Í B), e che: AÈB = (A-B)È (B-A)È(AÇB), i tre insiemi che compaiono nel RHS della precedente identità risultando a due a due disgiunti (abbiamo introdotto un'abbreviazione assai comoda, che sta per right hand side = parte destra; analogo è il significato di LHS, left hand side).

Nei primi due casi, e nel quarto, si tratta di operazioni binarie, che richiedono cioè un doppio input, che va considerato a priori sempre ordinato nel tempo, ossia un primo input a cui segue un secondo input; nel terzo caso, invece, si tratta di un'operazione che potrebbe dirsi unaria (anche se è una parola poco "elegante").

Discutiamo adesso alcune proprietà delle precedenti operazioni.

La commutatività esprime la circostanza che il risultato dell'operazione è indipendente dall'ordine in cui vengono assegnati gli input. Questo è per esempio il caso dell'unione e dell'intersezione:

(I.9)  AÈB = BÈA   ;   AÇB = BÇA

(dove è sottintesa la quantificazione: " coppia di insiemi A e B),

ma non è il caso della differenza, dal momento che, in generale, risulta:

(I.10) A-B ¹ B-A .

(Perché solo "in generale"? Quali sono le possibili eccezioni? Vedi l'esercizio discusso tra breve).

Altre proprietà dell'unione e dell'intersezione, che scriviamo ancora in coppia (a sottolineare l'evidente dualismo che esiste tra le due operazioni).

Associatività:

(I.11)  AÈ(BÈC) = (AÈB)ÈC   ;   AÇ(BÇC) = (AÇB)ÇC

(dove è sottintesa la quantificazione: " terna di insiemi A, B, C).

[Si constati che, al contrario, l'operazione di differenza non è associativa, ossia che non risulta, ovviamente in generale: A-(B-C) = (A-B)-C, del che ci si persuade facilmente attraverso esempi.]

Idempotenza:

(I.12)  AÈA = A   ;   AÇA = A

(dove è sottintesa la quantificazione: " insieme A).

Distributività (dell'unione rispetto all'intersezione, e dell'intersezione rispetto all'unione):

(I.13) AÈ(BÇC) = (AÈB)Ç(AÈC)   ;
AÇ(BÈC) = (AÇB)È(AÇC) .

(dove è sottintesa la quantificazione: " terna di insiemi A, B, C).

Dalla distributività, e dalle ovvie:

(I.14) A Í B Û AÈB = B Û AÇB = A,

si deducono infine le seguenti leggi di assorbimento:

(I.15) AÈ(AÇB) = A   ;   AÇ(AÈB) = A .

Quel dualismo tra unione e intersezione al quale si è fatto cenno, si precisa anche attraverso le seguenti proprietà della complementazione (corrispondenti evidentemente a proprietà logiche generali - negazione dell'et e del vel):

(I.16') " insieme A, e " X, Y Î P(A) Þ CA(XÈY) = CA(X)ÇCA(Y),

e "dualmente":

(I.16'') " insieme A, e " X, Y Î P(A) Þ CA(XÇY) = CA(X)ÈCA(Y) .

Le (I.16) esprimono formalmente l'ovvia circostanza di natura logica, già notata, secondo cui la negazione del quantificatore " è il quantificatore $, e inversamente che la negazione del quantificatore $ è il quantificatore ". Si può cogliere l'occasione per osservare che i sei simboli logici "essenziali" (diversi cioè da parentesi, barre, etc., che sono abbreviazioni del linguaggio ancora più semplici), vale a dire: " , $ , Ú , Ù , Ø , Þ , risultano in effetti sovrabbondanti. Oltre a quanto appena osservato, si rammenti che pure et e vel risultano tra loro collegate tramite il simbolo di negazione, e che l'implicazione p Þ q equivale logicamente alla Ø[(pÙ(Øq)], oppure, usando il vel anziché l'et: (Øp)Úq. Basterebbero quindi solo tre "segni" dei sei, per esempio " , Ú , Ø , ma si tratta di una "economia di pensiero" che ci sembra inopportuna sotto vari punti di vista: poiché l'uomo non è una macchina (per esempio, il suo intelletto "soffre" enunciazioni - e "dimostrazioni", o "comunicazioni" in genere! - troppo lunghe; il tempo di una vita è del resto un "tempo finito"), ecco che un eccesso di "riduzionismo" è quasi sempre controproducente ai fini della "chiarezza" della comprensione.

Notiamo inoltre che, mentre unione e intersezione sono operazioni che godono della proprietà che abbiamo chiamato idempotenza, la complementazione gode di quella che si chiama involutorietà. Ovvero, si tratta di un'operazione unaria che, come la negazione, ripetuta due volte su uno stesso elemento, fa tornare al punto di partenza:

(I.17) " X Î P(A) Þ CA(CA(X)) = X .

La ricerca delle naturali proprietà della differenza può essere ormai lasciata per esercizio al lettore, e comunque il nostro scopo non è di elencare subito tutte le proprietà che potrebbero tornarci utili nel seguito, riservandoci di tornare sopra uno stesso argomento quando necessario. [Pierre de la Ramée (1515-1572), noto anche con il nome latino Petrus Ramus, <<ben prima di Descartes proclamò l'impero della ragione sul principio d'autorità; in conseguenza insorse contro il feticismo per Aristotele e poi contro la cieca adorazione per Euclide. [...] Per esempio nella più celebre delle sue opere scientifiche - le Scholae mathematicae - egli osservò quanto fosse didatticamente opportuno il distribuire gli assiomi e i postulati nel corso dell'opera, invece di accatastarli nell'esordio come fece Euclide>> - da: Gino Loria, Storia delle matematiche - Dall'alba della civiltà al tramonto del secolo XIX, 3 voll., Torino, 1929-33, riediti in un unico volume da Cisaplino-Goliardica, 1982.]

Analogamente, sempre come esercizio può chiedersi di trovare la risposta alla seguente semplice domanda: quand'è che risulta A-B = B-A?

Risposta (da guardare solo dopo che ci si è un po' sforzati di provare da soli):
[(A-B) = (B-A)]Ù[(A-B)Ç(B-A) = Æ] Þ [(A-B)Ç(B-A) = (A-B) = (B-A) = Æ (per idempotenza)] Þ [(A Í B)Ù(B Í A)] Þ A = B.

Sono state così mostrate diverse applicazioni della teoria degli insiemi interne alla nostra materia, ma in conformità alle premesse "filosofiche" che abbiamo enunciato, gli infiniti esempi di sua presenza, e delle leggi della logica generale, dovrebbero in effetti essere tratti da un ambito appunto generale, e non da quello specifico della matematica, come è viceversa usuale nei testi scritti dai cultori di tale disciplina. Diamo allora un esempio di analisi testuale evangelica, mettendo due celebri affermazioni a confronto.

Nel vangelo di Luca 9,50 (il primo numero si riferisce al capitolo, il secondo al verso), troviamo scritto: <<qui enim non est adversum vos, pro vobis est>>, ovvero <<chi non è contro di voi è con voi>>. Tale affermazione si trova tale e quale in Marco 9,40, mentre ancora Luca, in un altro passo (11, 23), si esprime in modo "diverso": <<qui non est mecum contra me est>> (<<chi non è con me è contro di me >>). Tale brano è riportato tale e quale in Matteo 12, 30. Si tratta di affermazioni certamente diverse dal punto di vista letterale-testuale, ma dal punto di vista del loro significato? La psicologia ordinaria avverte in effetti una differenza: la prima appare benevola, "aperta", la seconda restrittiva, "chiusa" (in effetti da essa prende fondamento l'opinione: extra Ecclesiam nulla salus, non c'è salvezza per coloro che non fanno parte della Chiesa, salvo poi a stabilire quale sia la Chiesa "giusta").

Ma cerchiamo di vedere se le cose stanno proprio così, ovvero se le due affermazioni sono logicamente differenti. Entrambe si riferiscono ovviamente all'insieme dei cristiani, di coloro che hanno "fede" nel Cristo, diciamolo F, un insieme che deve essere concepito come un sottoinsieme dell'insieme U di tutti gli esseri umani (un insieme piuttosto "astratto"), ovvero: F Í U. Ad esso viene affiancato l'insieme di coloro che ai cristiani (o al Cristo) sono <<contrari>>, <<avversi>> (con il senno di poi, per esempio, coloro che perseguitarono i cristiani), diciamolo A (per non confondere con l'iniziale C di "complementare", un simbolo che dovremo presto introdurre in questa discussione). Ciò premesso, la prima affermazione si può formalizzare nel modo seguente:

" x Î U, x Ï A Þ x Î F,

la seconda:

" x Î U, x Ï F Þ x Î A.

Sono le due affermazioni semanticamente diverse? In virtù delle leggi della logica generale esse sono semplicemente la medesima affermazione. Infatti, scrivendo Ø(x Î A) in luogo di x Ï A, e lo stesso per x Ï F, le due affermazioni precedenti si scrivono rispettivamente come: Ø(x Î A) Þ x Î F  e  Ø(x Î F) Þ x Î A, sicché, in virtù della (I.4):

[Ø(x Î A) Þ x Î F] Û [Ø(x Î F) Þ Ø(Ø(x Î A))],

d'onde la conclusione (si rammenti l'involutorietà della negazione).

Può essere un utile esercizio, a un livello iniziale in cui lo studente deve prendere ancora confidenza con un linguaggio e un simbolismo che possono a prima vista apparire ostici, dimostrare che quanto appena asserito si può anche esprimere attraverso alcune semplici "equazioni" di teoria degli insiemi.

[" x Î U, x Ï A Þ x Î F] Û [CU(A) Í F],

anzi, poiché è sottinteso a priori che sia F Ç A = Æ (il che equivale a dire che sussistono le seguenti due inclusioni: [F Í CU(A)] Ù [A Í CU(F)]), ecco che abbiamo anche addirittura:

[" x Î U, x Ï A Þ x Î F ] Û [CU(A) = F].

Del tutto analogamente:

[" x Î U, x Ï F Þ x Î A] Û [CU(F) Í A],

la quale, unita all'inclusione A Í CU(F), che si è detto essere sempre valida a priori, fornisce infine:

[" x Î U, x Ï F Þ x Î A] Û [CU(F) = A].

Come esercizio, si utilizzi per esempio l'involutorietà (I.17) per dimostrare che i due asserti CU(A) = F, CU(F) = A sono identici come asserito:

CU(A) = F Þ CU(CU(A)) = CU(F) Þ A = CU(F) ;
CU(F) = A Þ CU(CU(F)) = CU(A) Þ F = CU(A)) .

Perché allora quell'indubitabile effetto psicologico, che induce a ritenere "differenti" le due dichiarazioni? A parte il fatto che sostenere in una "tesi" che qualcuno sia <<contro>> qualcosa suona "aggressivo" a orecchie le quali non gradiscono che si sottolinei l'esistenza di "conflitti" (un effetto che la "stessa" proposizione non provocherebbe qualora la tesi venisse espressa in una forma conciliante, come è senz'altro quella confortante che ci informa che qualcuno almeno <<è con noi>>; un modo diverso di esprimere il medesimo concetto, che è sovente possibile raggiungere giocando sulla (I.4)), riteniamo che si tratti qui piuttosto dell'aspettativa dell'ascoltatore. In effetti, ciò che taluni si attendono dalle parole in esame è che attraverso di esse venga stabilita una precisa bipartizione (che la mentalità "pratica" considera ovviamente essenziale) nell'insieme U degli esseri umani: "salvi" (il cui insieme indicheremo con S, S Í U) e "dannati" (un insieme D Í U); ovvero, agnelli e capri, coloro che il giorno del giudizio saranno alla destra del Padre o alla sua sinistra. Le due affermazioni che stiamo analizzando sono invero perfettamente coerenti con questo punto di vista dicotomico (che divide in due), dal momento che, così come U risulta adesso l'unione di due sottoinsiemi disgiunti,
U = SÈD, lo stesso insieme U veniva dianzi decomposto nell'unione di altri due (a priori diversi) sottoinsiemi pure disgiunti, U = FÈA, con la naturale suggestione che si trattasse della medesima bipartizione, ovvero che: F = S,
A = D. E' noto però che l'umana pietà ama poco codeste rigorose dicotomie, tanto è vero che, per esempio, ha introdotto apposta concetti quali il Purgatorio, (per attenuare la contrapposizione Paradiso-Inferno che incute timore; qualche teologo si è spinto addirittura a ipotizzare che l'infinita bontà del Dio che lui concepisce sarà poi di fatto tale da rendere l'insieme D vuoto, un insieme che sarebbe quindi da ritenersi vuoto come l'Inferno), o il Limbo (si rammentino le discussioni relative alla sorte delle persone "buone" che avevano l'unico torto di essere vissute prima dell'"incarnazione"). La persona pietosa sostituisce allora alla bipartizione {F, A} una tripartizione, introducendo (senza bisogno di chiedere lumi a nessuno, fosse anche il figlio di Dio), che l'insieme degli esseri umani va logicamente tripartito tramite l'insieme F degli "eletti", quello A di coloro che sono stati proprio e irrimediabilmente cattivi nei loro confronti (caso paradigmatico: Nerone, un personaggio forse un po' calunniato dalla storia), e un terzo insieme I (la lettera I sta per l'iniziale di "indifferenti"), nel quale vanno inclusi coloro che sospendono il giudizio sulla delicata questione, oppure hanno un giudizio negativo nei confronti di chiacchiere "celesti", ma non lo mettono in pratica con cattive azioni nei confronti dei "teomani". La presenza di queste due partizioni può indurre in effetti in qualche fraintendimento, perché quando si mette a confronto la tripartizione {F, A, I} (invero del tutto "logica") con la bipartizione fondamentale {S, D}, ecco che la prima affermazione, quella "bonaria", viene interpretata come:

" x Î U, x Ï A Þ x Î S, e quindi I Í S (in questo caso il figlio di Dio conforterebbe gli interlocutori pietosi, o quelli più tiepidi, scettici, con una prospettiva rassicurante),

mentre la seconda come:

" x Î U, x Ï F Þ x Î D, e quindi I Í D (in questo caso il figlio di Dio si comporterebbe invece come un giudice inflessibile, spedendo gli ignavi ad arrostire per l'eternità insieme a Nerone).

In un caso, quei soggetti che si trovano in I vengono salvati, nell'altro vengono dannati, ed è chiaro che almeno per loro (e per i loro amici) la differenza tra le due dichiarazioni (o minacce) sarebbe assai significativa. Ci sembra che solo in questo modo si possa spiegare perché taluni percepiscano segni di "schizofrenia", in verità del tutto inesistente, in due affermazioni che sono invece perfettamente equivalenti. Ripetiamo che la contraddizione sarebbe stata invece presente qualora una volta si fosse sostenuta l'inclusione I Í S, un'altra l'inclusione I Í D, a meno che naturalmente I non sia da ritenersi vuoto (ipotesi che è del resto corrispondente al testo evangelico), ma, a parte il fatto che una siffatta ipotesi appare inverosimile (ovviamente, secondo una mentalità che non accetta la proposta dicotomia), non si vedrebbe allora la convenienza di introdurre un terzo insieme, destinato a rimanere puramente "potenziale". La "confusione" non è quindi nelle parole della "buona novella", ma soltanto nella mente di chi cade in equivoco sovrapponendo il proprio pensiero a quello dell'interlocutore, e crede di avere fatto opera di sintesi coerente senza aver abbastanza curato la formalizzazione dei concetti, o degli enunciati su cui opera. Si tratta di quelle <<persone che, in tutta la loro vita, non percepiscono nulla come è necessario per bene giudicarne>>, e che talvolta si poggiano in malafede su simili fraintendimenti per interpretare un testo (questo o altri) come loro meglio aggrada.

Quello che abbiamo voluto a lungo analizzare è un esempio che, a prescindere dall'eventuale interesse specifico, ci suggerisce comunque di introdurre in modo "rigoroso" alcuni importanti concetti, con i quali chiudiamo questa prima parte del capitolo I. Dato un qualsiasi insieme non vuoto A, un sottoinsieme (che risulterà certamente non vuoto) P Ì P(A) si dice una partizione di A (attenzione alle due diverse iniziali che qui sono in conflitto, sebbene in maniera sopportabile: P come partizione, P come parte) quando gli elementi di P siano:

(i) tutti diversi dall'insieme vuoto;
(ii) a due a due disgiunti;
(iii) la loro unione sia l'intero A.

Si osservi che unione e intersezione si possono ovviamente estendere, dal caso di due input, a quello di una totalità qualsiasi di insiemi, e che avevamo in effetti già utilizzato tale possibilità nel parlare dell'intersezione di tutti gli insiemi delle parti P(X), al variare di X. Nel presente contesto, si tratta comunque di utilizzare la nozione per sottoinsiemi di un dato insieme A, ossia per elementi di un fissato P(A).

[Quanto precede si presta a qualche puntualizzazione. Comunque dato un certo sottoinsieme S di un fissato insieme delle parti P(A) di un fissato insieme A, possiamo introdurre i seguenti due sottoinsiemi di A:
ÈA(S) = {" x Î A ½ ($ C Î S : x Î C)}
ÇA(S) = {" x Î A ½ (" C Î S Þ x Î C)},
che si dicono rispettivamente l'unione, o l'intersezione, degli elementi di S (l'indice A è opportuno per ricordare che il risultato dell'operazione è un sottoinsieme di A; si noti bene che invece S è un sottoinsieme di P(A)). In virtù di tale definizione, risultano per esempio tutte chiaramente valide le seguenti asserzioni: ÈA(P(A)) = A; ÇA(P(A)) = Æ;
" X Í A Þ ÈA({X}) = X (si presti bene attenzione al fatto che: " X Í A Þ {X} Í P(A));
" X Í A Þ ÇA({X}) = X ; " S Î P(A) Þ CA(ÈA(S) = ÈA(CA(S));
" S Í P(A) Þ CA(ÇA(S) = ÈA(CA(S));
nell'ultima delle quali CA(S) designa l'insieme dei complementari in A degli elementi di S, e quindi costituisce ancora un sottoinsieme di P(A), che non ha nulla a che fare però con CP(A)(S). Abbiamo detto che tutto quanto precede è logicamente assai chiaro, ma qualche meditazione a parte la merita il solito caso del "vuoto"! Qui esso appare ben due volte, la prima come semplice sottoinsieme di P(A), sicché hanno senso entrambe le espressioni: ÈA(Æ) e ÇA(Æ), le quali valgono rispettivamente Æ e A. Mentre la prima appare piuttosto comprensibile, in virtù della definizione stessa di ÈA, una lunga esperienza didattica ci informa che di solito non è questo il caso della seconda (anche se pur essa si può comprendere "logicamente"). Chi ne ha bisogno, potrà forse convincersi meglio della validità della: ÇA(Æ) = A, attraverso la catena di identità: CA(ÇA(Æ)) = ÈA(CA(Æ)) = ÈA(Æ) = Æ (per comprendere chi è CA(S), bisogna pensare a tutti gli elementi di S, e farne i complementari in A; se S = Æ, ecco che pure CA(S) = Æ). Il secondo caso in cui compare l'insieme vuoto è sotto forma del singleton {Æ}, in quanto non solo Æ Í P(A) (eventualità che abbiamo già esaminato), ma anche Æ Î P(A). Si hanno adesso le seguenti identità: ÈA({Æ}) = Æ ; ÇA({Æ}) = Æ ; perfettamente coerenti con le identità generali che avevamo già stabilito poc'anzi nel caso di un sottoinsieme di P(A) che fosse un singleton.]

Se ci si limita soltanto all'ultima condizione enunciata, lasciando cadere le prime due, si dice che l'insieme P è un ricoprimento di A, nel qual caso A, o un elemento di P, possono anche essere il vuoto. Si noti allora che la specificazione restrittiva iniziale P Ì P(A) è senz'altro corretta nel caso di una partizione (P non può coincidere con l'intero P(A), perché c'è almeno l'insieme vuoto che è contenuto in P(A) ma non in P), mentre che la precedente inclusione sia propria non è richiesto (così come non è richiesto che sia A ¹ Æ) nel caso di un ricoprimento; anzi, P(A) stesso è manifestamente un ricoprimento, ancorché "banale", di A.

P si chiama anche un insieme quoziente di A (si veda il commento a tale denominazione che viene effettuato nella nota precedente la (III.55)). Osserviamo esplicitamente che esso appare sempre più piccolo di A (un concetto importante che naturalmente preciseremo nel seguito), a volte molto più piccolo di A, per esempio quando A è infinito e P è finito (per esempio, la classica bipartizione tra numeri naturali pari e dispari; oppure, la tripartizione che resta indotta in un piano da una retta in esso contenuta; l'insieme quoziente è formato nel primo caso da due soli elementi, nel secondo da tre, che sono due semipiani "aperti" con una comune "frontiera", più la retta di cui trattasi). Tra gli insiemi quoziente di A ce ne sono due "universali", e in qualche modo entrambi banali: P = {A}, che è uno di quegli insiemi che abbiamo chiamato singleton, e P = {{a}, per " a Î A}, cioè la totalità dei singleton che sono in P(A). Nel secondo caso, nel contesto di possibili raffronti tra A e P, P coincide "sostanzialmente" con A, un modo di dire su cui torneremo meglio nella seconda parte del presente capitolo (nella quale approfondiremo pure adeguatamente l'importantissimo concetto di partizione, ossia di insieme quoziente).

Si noti adesso che:

(I.18) Una partizione P' non può mai essere contenuta propriamente in un'altra partizione P, per esempio P' Ì P.

Dim. Supponiamo che C sia un elemento di P non contenuto in P'. Poiché C non è vuoto, esistono almeno un elemento x Î A tale che x Î C, e un elemento
C' Î P' tale che x Î C' (poiché P' "ricopre" A). Ecco allora che CÇC' ¹ Æ, e quindi C' = C (poiché gli elementi di P sono a due a due disgiunti, e C' Î P per ipotesi), il che è assurdo perché si è supposto che C Ï P'. ä (simbolo che useremo come "fine dimostrazione").

Nonostante (I.18), esiste un modo naturale di mettere tra loro a confronto delle partizioni. Una partizione P' si dice meno fine (propriamente oppure no) di P, e si può usare il simbolo P' Ð P (P' ÐÐ P se P' è propriamente meno fine di P), quando: " C Î P Þ $ C' Î P' ½ C Í C'. Corrispondentemente, P si dice più fine di P', e la stessa terminologia si introduce nel caso dei ricoprimenti. Il singleton {A} rappresenta naturalmente la partizione meno fine di tutte (minima), mentre P = {{a}, per " a Î A} rappresenta quella più fine di tutte (massima).

Ciò premesso, è "evidente" che (si ritorni alla Dim. (I.18)):

(I.19) Fissate le precedenti notazioni, esiste un unico C' Ê C per ogni dato C, e P' può quindi essere ottenuta da P sostituendo ad alcuni "blocchi" di P la loro unione.

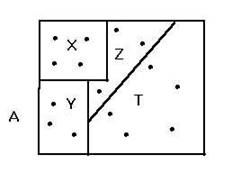
(Fig. I.20)

Nella figura compare una 4-partizione P di un insieme A con 15 elementi,
P = {X, Y, Z, T} (i sottoinsiemi X etc. sono stati disegnati volutamente "diversi" per non favorire la concezione errata che i blocchi di una partizione debbano essere sempre costituiti da uno stesso numero di elementi; qualche volta potrebbero esserlo, qualche volta no, e tanto nel caso finito quanto nel caso infinito, quando si saprà come "calcolare" il numero degli elementi di un insieme infinito), la quale dà origine per esempio a una 3-partizione P' strettamente meno fine di P: P' = {X, Y, ZÈT}, oppure alla 2-partizione
P'' = {XÈY, ZÈT}, anch'essa strettamente meno fine di P. Anzi, risulta:
P'' ÐÐ P' ÐÐ P. E' chiaro inoltre che, data una partizione P' meno fine di una data partizione P di un insieme A, P' induce una corrispondente partizione di P, definita come quella partizione P'* di P i cui elementi siano gli insiemi di quei blocchi di P che vanno a costituire un unico blocco di P'. Un esempio adeguato vale più di mille parole: fermo restando il significato dei simboli precedenti, è chiaro che: P'* = {{X}, {Y}, {Z, T}}, mentre P''* = {{X, Y}, {Z, T}}.

Diamo un esempio di tutto ciò riferendoci ancora alla discussione evangelica di poc'anzi. Abbiamo detto che il dilemma poteva riassumersi nel fatto che una bipartizione di U, P' = {S, D}, veniva messa a confronto, secondo un'opinione comune poco attenta alle parole del Cristo, con una tripartizione P = {F, A, I} dello stesso insieme U. Nel caso benevolo si aveva S = FÈI, D = A, e quindi P' poteva dirsi una partizione meno fine di P, ottenuta mediante la seguente partizione di P: P'* = {{F, I}, {A}}. Nel caso più severo (cioè: S = F, D = AÈI), P' costituiva ancora una partizione meno fine di P, ottenuta però mediante la seguente partizione di P: P'** = {{F}, {I,A}}, ed era quindi una bipartizione diversa dalla precedente P'. Tutto questo ci sembra confermare l'opinione che, sebbene si tratti di concetti "elementari", ad essi occorre prestare la necessaria attenzione, allo scopo di non fare confusione.

Qualche parola conclusiva può essere spesa sin da ora per sottolineare come le partizioni siano ovviamente da riferirsi all'operazione logica di classificare, un'esigenza naturale di ogni teoria della conoscenza, ideale o empirica. Classificare significa in qualche senso "fare ordine" all'interno di un insieme possibilmente eterogeneo, rilevando l'esistenza di particolari omogeneità tra i suoi elementi. Oggetti diversi possono essere distinti per differenze, oppure uniti per somiglianze. Tanto per dire, nell'esempio "teologico" di prima, l'individualità di un singolo essere umano diveniva secondaria rispetto alla sua appartenenza all'insieme S o all'insieme D. Si può aggiungere che il classificare non è l'unico metodo seguito per mettere in pratica il proposito di fare ordine, e cioè che esso può essere ottenuto anche mediante filtrazioni. Per il momento basterà illustrare cosa si può intendere per filtrazione finita (e propria) di un insieme non vuoto A. Si tratta di un sottoinsieme finito e non vuoto F di P(A) (un'iniziale F che adesso sta per "filtrazione", e non per "fede"!), costituito quindi da certi k elementi (k = 1, o k = 2, etc.), diciamoli F1, F2,..., Fk, che si possano "ordinare" in maniera tale che risulti:

A = F1 É F2 É ... É Fk .

Ad una siffatta filtrazione si può peraltro sempre associare una partizione, e precisamente: {F1-F2, F2-F3,..., Fk-1-Fk, Fk}, se Fk ¹ Æ, altrimenti basta finire un passo prima: {F1-F2, F2-F3,..., Fk-1-Fk (= Fk-1)} (poiché tra la seconda partizione e la prima non c'è sostanziale differenza, possiamo aggiungere senza perdere di generalità l'ipotesi che ogni elemento della filtrazione sia diverso dal vuoto, come si è già richiesto per i blocchi di una partizione).

Lo studente non dovrebbe faticare a comprendere meglio tali concetti, individuando gli esempi a lui noti di filtrazione, e immaginando la possibilità di ricorrere simultaneamente, sempre allo scopo di "fare ordine" in un dato insieme (in una data "fenomenologia"), sia a filtrazioni che a partizioni. Tutte questioni che potranno essere sempre meglio analizzate, quando cresceranno le possibilità offerte dal "linguaggio" che stiamo gradatamente presentando-costruendo. [Perché la teoria degli insiemi, o meglio la teoria degli insiemi e delle funzioni, non è altro che un modo conveniente per "parlare" di certe cose in modo "rigoroso". La difficoltà didattica di un corso preliminare come questo è di riuscire a mantenere un certo equilibrio tra la tentazione di portare avanti lo studio del linguaggio senza corrispondente opportuna fenomenologia, che del linguaggio mostri adeguatezza e utilità, e la difficoltà di discutere la fenomenologia senza ancora possedere uno strumento efficace allo scopo.]

(I.21) Nota. Questo è un corso nel quale si discuterà molto di strutture, sicché il consueto capitolo iniziale dedicato alla "teoria degli insiemi" viene detto riferirsi ai semplici insiemi "privi di struttura", anche se in alcuni di essi, data l'essenza specifica (ontologica) dei loro elementi, è impossibile non riconoscere l'emergenza di alcune strutture "spontanee" (per esempio in N); in casi assai più frequenti, delle strutture assai rudimentali, che cominciano ad apparire collegate agli elementi dell'insieme in maniera che diremo naturale. Si tratta di un fenomeno secondo noi filosoficamente rilevante, al quale ci piace qui cominciare ad accennare, notando per esempio la differenza tra quegli insiemi che ammettono una bipartizione naturale (che potrebbero chiamarsi decomponibili), e quelli che al contrario non l'ammettono (indecomponibili). Poiché ogni insieme A che non sia un singleton ammette senz'altro una bipartizione (ovviamente: A ¹Æ), ecco che tutto il significato di una siffatta distinzione si fonda allora sul significato che dev'essere attribuito a quell'aggettivo qualificativo "naturale", cui pure faremo largo ricorso. Siamo di fronte a una caratterizzazione significativa, che può essere decisa unicamente dalla logica della ragione, conformemente alla riflessione di Federigo Enriques citata in Introduzione. Siamo in effetti di fronte a un problema che riguarda l'essenza delle "cose", e il "nome" delle cose (si ricordino per esempio i nostri tre geniali comici Aldo, Giovanni e Giacomo, quando nello sketch dei "sardi" danno pedantemente un nome a ogni noce, a ogni fiocco di neve, etc.). I due casi estremi che bisogna contemplare sono l'insieme di quei numeri che abbiamo visto si dicono appunto naturali,
{1, 2, 3,...}, dove ogni numero ha un nome ed è perfettamente distinguibile da ciascun altro (ogni sottoinsieme di N che non sia un singleton è decomponibile!), e lo spazio ordinario S, dove nessun punto ha (può avere) un "nome", e gli elementi dell'insieme sono tutti sostanzialmente "uguali" a ciascun altro (ma anche i segmenti di una retta, o le semirette di una retta, "chiuse" o "aperte", sono per esempio insiemi che si presentano all'intelletto omogeneamente, seppure in modo leggermente diverso, come diremo in fine di nota). Tali esempi dimostrano che, se si volesse obiettare che la distinzione proposta è soggettiva, relativa per esempio allo stato dell'informazione del soggetto che è chiamato a decidere se un determinato insieme sia o no indecomponibile, essa assume particolare importanza nel caso di insiemi "universali", rispetto ai quali cioè lo stato della conoscenza può ritenersi "perfetto" in ogni intelletto umano. Potremmo concludere questa prima esposizione di un ambito d'idee poco frequentato, introducendo la nozione di insieme decomponibile in senso stretto, intendendo con ciò un insieme che sia decomponibile mediante una bipartizione naturale, nella quale sia inoltre possibile distinguere in modo pure naturale un primo elemento della partizione da un secondo. Tutti gli insiemi che non sono decomponibili in senso stretto potrebbero dirsi omogenei, o se si preferisce "democratici"! Una specificazione sottile, ma non di poco conto: per esempio, l'insieme delle semirette di una retta (diciamo per esempio chiuse) ammette una bipartizione naturale, che distingue quelle orientate in un certo verso da quelle orientate nell'altro, ma la natura delle due classi di semirette che così si ottengono induce a ritenere che la totalità intera di esse formi un insieme che è sì decomponibile, ma che non è decomponibile in senso stretto. Per contro, l'insieme dei segmenti appare invece proprio indecomponibile tout court (e informiamo subito che tale enunciato risulta essere addirittura equivalente al celebre V postulato di Euclide sulle parallele, ispiratore delle cosiddette geometrie non euclidee, che tanta influenza - non sempre positiva - hanno avuto e continuano ad avere anche in corsi di matematica "elementare" come il presente; si veda quanto se ne dice nello stesso sito che ospita queste dispense). Chiudiamo davvero osservando che quella che precede costituisce un esempio di classificazione (di tutti gli insiemi) effettuata prima per partizione (dicotomica), decomponibili-indecomponibili, e poi per filtrazione: {insiemi decomponibili} É {insiemi decomponibili in senso stretto}.

(I.22) Digressione. Possiamo infine tornare sulla "questione di senso" che avevamo cominciato a trattare introducendo il concetto "intuitivo" di "universo".

[in fase di completamento]

 

Parte II - Funzioni

 

Allo stesso modo primitivo che quello di insieme consideriamo il pur più complesso concetto di funzione. Noi diremo esattamente che abbiamo una funzione, è definita una funzione, è assegnata una funzione, ci troviamo di fronte a una funzione, e chiamiamola pure f, quando ricorrono TUTTE E TRE le seguenti condizioni:

(i) è fissato un insieme di input (termine oggi usuale, potremmo dire in italiano "entrate") della funzione f, che chiameremo dominio di f, indichiamolo per esempio con la lettera A, e se si vuole scriveremo, con ovvia stenografia:
A = dom(f);

(ii) è fissato un insieme di output ("uscite") di f, che chiameremo codominio di f, indichiamolo per esempio con la lettera B, B = codom(f);

(iii) è fissata una legge, o regola, in qualche modo "chiara e distinta", la quale consente di costruire, a partire da un input assegnato in modo ARBITRARIO in A, un UNICO output ad esso corrispondente, o associato tramite f, in B.

Modi di esprimere una funzione f da A a B, o da A in B, o da A verso B.
f: A ® B, oppure  A  B , con il "nome" della funzione che appare sopra la "freccia". La specificazione dell'output y Î B della funzione per un certo input x Î A, si esprime per esempio attraverso l'identità y = f(x); oppure, si riporta sotto al simbolo della funzione il simbolo: x  y (si noti che questa nuova particolare freccia è diversa dalla precedente; del resto, A e B sono insiemi, mentre x ed y sono soltanto elementi di insiemi; ® è un simbolo funzionale,  non lo è). Esempio:
f: A         ®          B
x Î A          y = f(x) Î B .

[E qui è opportuna una precisazione, in ordine a quel termine "regola", che potrebbe indurre in qualche equivoco. Illustriamo la situazione con un esempio. Supponiamo di avere un insieme A costituito diciamo da tre studenti, indichiamoli con le lettere x, y, z, e di voler definire una funzione da A = {x, y, z} all'insieme I dei due "concetti" Vero, Falso:
I = {Vero, Falso} (sintetizziamoli con le lettere V, F, rispettivamente), mediante la seguente "procedura": se x è biondo, associamo ad x il simbolo V, altrimenti il simbolo F. Supponiamo che y sia l'unico studente biondo tra i tre, ossia che la regola in parola permetta di individuare le seguenti "associazioni": x  F, y  V, z  F. Bene, introduciamo adesso, mantenendo inalterati i nostri "dominio" e "codominio", un'altra regola, indubitabilmente diversa da quella precedente. Precisamente, assoceremo a un elemento di A la lettera V se egli risulta nato a Roma, e la lettera F altrimenti. Facciamo l'ipotesi che questa nuova regola individui le seguenti "associazioni": x  F, y  V, z  F, vale a dire le stesse identiche di prima. L'unico studente biondo dei tre, y, è anche l'unico ad essere nato a Roma. Le regole in esame sono certamente diverse, ma la funzione f : A ® I da A ad I che ne consegue è la stessa. La funzione cioè non coincide con l'algoritmo, o il predicato verbale, con cui essa è stata costruita (cogliamo l'occasione per introdurre dei sinonimi per "regola"), ma unicamente con il suo effettivo manifestarsi: x  F, y  V, z  F è una funzione,
x  V, y  V, z  F è un'altra funzione (e in tutto ne possiamo trovare solo 8 di questo "tipo"). In altre parole ancora, una funzione deve essere concepita soltanto come: 1 - il dato del dominio; 2 - il dato del codominio; 3 - un "elenco" di tutti gli elementi del dominio, a ciascuno dei quali viene "affiancato" uno ed un solo elemento del codominio, punto e basta, indipendentemente da eventuali "descrizioni" che permettono di individuare, specificare, illustrare, tale elenco, ma non sono la funzione. (Ci si occuperà più avanti in maggiore dettaglio di funzioni della natura delle precedenti, che si chiamano funzioni caratteristiche sull'insieme A, dopo che avremo però fissato "canonicamente" come codominio l'insieme
{1, 2}, e volendo continuare a mantenere la precedente "interpretazione", convenendo per esempio che sia: 1  V, 2  F).]

Esercizio: si esprima, con il linguaggio della logica generale, l'identità tra due funzioni f e g:
(f = g) Û [dom(f) = dom(g) = A]Ù[codom(f) = codom(g) = B]Ù[" x Î A Þ
Þ f(x) = g(x)].

Tutte le funzioni di dominio A e codominio B possono essere chiamate a costituire un unico nuovo insieme, che si indica con il simbolo H(A,B) (un'iniziale "H" della cui origine diremo in seguito).

Come ci sono i sinonimi di insieme, ci sono pure quelli di funzione, che può dirsi infatti: applicazione, corrispondenza, rappresentazione, trasformazione (utilizzato soprattutto in ambito geometrico), o, con un inglesismo, mappa (map), che rimanda concettualmente alla "rappresentazione" di una località su una carta geografica. Tra i sinonimi, particolarmente opportuno quello di morfismo, sia per motivi concettuali (una sorta di anticipazione della teoria delle categorie), sia, come ci persuaderemo presto, linguistici (permettendo le espressioni monomorfismo, epimorfismo, etc.). Particolarmente suggestivo (evocativo di un particolare contesto applicativo) è il termine famiglia, per cui si parla per esempio di una famiglia di elementi di un certo insieme A, oppure di una famiglia di parti (sottoinsiemi) di un certo insieme A. Una famiglia, di elementi o di parti di A, è dotata di un fissato insieme di indici I, ed è semplicemente una funzione, rispettivamente I ® A, oppure I ® P(A). Dato un indice i Î I, è comune indicare il corrispondente di i nella famiglia con un simbolo del tipo ai Î A, oppure, nel secondo caso, con un simbolo del tipo
Ai Î P(A). Un'evenienza pure molto comune è quella in cui I sia l'insieme N, nel qual caso si parla per esempio di una famiglia f in H(N,A) come di una successione di elementi di A, i quali si designano allora, anziché con la notazione f(1) = a1, f(2) = a2, etc., semplicemente come a1, a2, ... .

Osservazioni importanti

- Assoluto obbligo dell'ARBITRARIETÀ dell'input nel dominio: dato un qualsiasi elemento del dominio, deve essere possibile indicare chiaramente senza eccezioni chi è il (articolo determinativo) suo trasformato, o associato, tramite la funzione di cui trattasi (se x è l'input e f la funzione, si deve poter parlare dell'output y di x tramite f, ovvero di y = f(x), usando, come notato, l'articolo determinativo: lo studente principante dovrebbe fare sempre molta attenzione alla differenza tra articoli determinativi e indeterminativi).

- Assoluto obbligo dell'UNIVOCITÀ della funzione: dato un input, ci deve essere un unico output, ovvero, y = f(x) assieme a y' = f(x), con y ¹ y', non può assolutamente verificarsi.

[Per esempio, è illecito scrivere per una radice quadrata , come qualche volta s'usa, per esempio  = ±2, e pensare contemporaneamente alla  come a una "funzione", che vada per esempio dall'insieme dei numeri reali positivi a quello dei numeri reali tutti; se si vuol pensare alla radice quadrata come a una siffatta funzione, bisogna scrivere   = 2, e basta, mentre vedremo come si possa soddisfare, sempre utilizzando funzioni univoche, il desiderio di esprimere tutti i numeri reali tali che il loro quadrato sia uguale a 4; basterà considerare, con simbolismo autoevidente (R è un simbolo canonico che designa l'insieme dei numeri reali; citiamo adesso questi numeri anche se alla loro costruzione - indispensabile, perché NON si tratta di enti che possano legittimamente considerarsi primitivi - accenneremo appena alla fine del presente corso; ciò nonostante, ci permetteremo di trarre di tanto in tanto qualche esempio da essi desunto, o, se si vuole, dal parallelo corso di Analisi matematica), una funzione da R>0 a P(R), che potrebbe pure dirsi, anziché una funzione univoca da tali citati dominio e codominio, una funzione multivoca da R>0 a R, ma noi preferiremo sempre rispettare le convenzioni precedenti, e parlare costantemente di funzioni univoche, tra dominio e codominio che dovranno essere convenientemente precisati quando si tratti di descrivere certe determinate fenomenologie, come appunto quella della radice quadrata, ovvero della funzione immagine inversa della funzione quadrato - vedi il successivo punto (I.24).]

- Imprescindibilità della specificazione di dominio e codominio. Se uno studente parla di, pensa di conoscere, etc., una certa funzione f, ma non sa rispondere alle domande: "chi è il dominio di f?", "chi è il codominio di f?", in realtà non conosce perfettamente la funzione. I precedenti interrogativi debbono infatti avere una risposta UNIVOCA, pena la non completa identificazione della funzione di cui si vorrebbe parlare.

[Qualche volta si può invero essere indotti a trascurare tale aspetto, perché la specificazione, peraltro assolutamente necessaria in linea di principio, viene in realtà sottintesa dal particolare contesto in esame. Per esempio, delle funzioni che sono oggetto di studio in Analisi matematica si assegna spesso la sola "regola" di deduzione input ® output, visto che i loro "argomenti" sono, almeno inizialmente, dei semplici numeri reali. Nei casi più elementari, si tratta proprio di un comune dominio e codominio coincidenti con la totalità dei numeri reali: A = B = R (si noti bene che nessuno ha escluso infatti nella precedente "definizione" di funzione tale possibilità, dom(f) = codom(f), e che bisognerà tenere presente che in matematica, come altrove, vigerà sempre la norma: ciò che non è proibito è permesso, fatta salva la facoltà di proibire DOPO quello che ci siamo dimenticati di proibire PRIMA!), mentre nei casi meno elementari diventa più interessante andare a ricercare quali possano essere i domini ammissibili per certe "regole", ed un eventuale dominio massimo (che si dice il campo di definizione della "funzione").]

- Analogamente, e va da sé, dato un qualsiasi input x Î dom(f), bisogna essere in grado di specificare con assoluta precisione quale sia l'unico output
f(x) Î codom(f), ovvero quale sia la regola di trasformazione input ® output, pena al solito la non completa identificazione della funzione di cui si tratta. (Nella pratica, tale prescrizione viene ad essere talvolta sfumata, qualora si introducano nel corso di un ragionamento alcune funzioni della cui esistenza si è in qualche modo "certi", ma che non si "danno" - è impossibile dare! - effettivamente; vedremo nel seguito numerosi casi in cui tale circostanza si concretizza).

- Chiudiamo con un esempio di possibile pedanteria nella specificazione tanto di dom(f), quanto di codom(f). Se si prende per esempio la ben conosciuta funzione trigonometrica coseno, simbolo cos(x), il cui argomento x può essere un qualsivoglia numero reale, bisogna specificare a rigore il dominio e il codominio di tale funzione, ed ecco che per esempio cos: R ® R è una precisazione accettabile. Del resto, sarebbe pure corretto scrivere
cos: R ® [-1,1], oppure, cos: [0,2p] ® [-1,1], dove p è il celebre numero reale che esprime il rapporto tra la lunghezza di una circonferenza e il suo diametro (si ricordi che [a,b], per due numeri reali a, b, con a < b, designa la totalità dei numeri reali x compresi tra a e b, ovvero: [a,b] = {" x Î R ½ a £ x £ b}), e in ciascuno dei casi riportati non si è "perduta" alcuna informazione sulla funzione coseno. A rigore però, dal punto di vista della teoria degli insiemi e delle funzioni, tutte queste dovrebbero essere considerate funzioni diverse, e si dovrebbero usare simboli diversi per designarle; ciò nonostante, e a ragione, è raro nella pratica spingersi fino a tanto, almeno quando, come nel caso esaminato, il contesto semantico, cioè quello di utilizzo degli enti matematici che intervengono in un certo discorso, non lasci spazio a fraintendimenti gravi. Ciò non toglie che dovremmo in ogni caso essere capaci di rendere un'argomentazione sempre più formalmente corretta, fino al limite della "perfezione", eliminando tutte le eventuali omissioni, semmai dietro richiesta (sottolineiamo ancora una volta, di altri o di noi stessi), e soprattutto capaci di comprendere il senso delle precisazioni sollecitate.

Così come ci siamo chiesti nel caso degli insiemi, potremmo chiederci adesso: quand'è che una funzione può essere considerata "assegnata"?, ma la risposta, da un punto di vista "ontologico", non potrebbe essere diversa da quella che abbiamo già fornito in occasione dell'analoga domanda. Tutti gli enti che entrano a far parte di un discorso matematico devono poter essere concepiti in maniera chiara e distinta, e del resto insiemi e funzioni vanno visti formare un unico "complesso", la loro "conoscenza" procedendo di pari passo. Le funzioni sono uno strumento con cui diversi insiemi (o anche uno stesso) si mettono in collegamento tra loro, ed esempi di esse tratti dall'ambito del "pensiero comune" sono ovviamente innumerevoli, a partire dalle funzioni "nome di una persona" (in generale il "nome" di una "cosa" è, in relazione a una fissata fenomenologia, una funzione tra l'insieme di certe cose e quello dei loro nomi), "luogo" o "anno" di nascita, ma funzioni sono anche tutte le specificazioni effettuate mediante l'introduzione di aggettivi qualificativi in un fissato insieme (una ragazza "bionda"), e così via. Il formalismo funzionale (precisazione del dominio e del codominio, univocità dell'output, etc.) serve solo a puntualizzare le modalità d'esercizio dello strumento logico.

Appellativi notevoli

- Una funzione f : A ® B si dice iniettiva (o un'iniezione), quando:
" x, y Î A, x ¹ y Þ f(x) ¹ f(y),
ovvero, in parole, quando input distinti hanno output distinti. Per le funzioni iniettive si utilizza a volte un simbolo speciale, f: A  B , con una seconda freccina all'inizio della barra orizzontale.

- Una funzione f : A ® B si dice suriettiva (o una suriezione), quando:
" z Î B, $ x Î A ½ z = f(x),
ovvero, in parole, quando ogni elemento z del codominio B della funzione è un output di qualche elemento x del dominio A della funzione. Per le funzioni suriettive si utilizza a volte un simbolo speciale, f: A  B , con una seconda freccina alla fine della barra orizzontale.

- Una funzione f : A ® B che sia simultaneamente iniettiva e suriettiva si dice biiettiva, o biunivoca (o una biiezione; è usuale parlare per esempio anche di una corrispondenza biunivoca tra due insiemi A e B). Per una biiezione
f : A ® B risulta evidentemente: " z Î B, $! x Î A ½ z = f(x), dove quel punto esclamativo apposto al quantificatore esistenziale $ significa appunto: "esiste ed è unico". Per le funzioni biunivoche si utilizza a volte un simbolo speciale,
f: A  B, ponendo una tilde "~" sopra al simbolo di funzione, per sottolineare la circostanza che i due insiemi A e B sono allora concepibili, per il tramite della funzione f, quasi uguali (un elemento di A corrisponde a un elemento di B, e un elemento di B proviene da un solo elemento di A). A questa "quasi uguaglianza" presteremo nel seguito attenzione particolare, ma diciamo subito che, sotto l'aspetto simbolico, si usa per esempio scrivere A @ B (a volte con una sola barretta orizzontale) per significare appunto che A è quasi uguale a B, in un senso che bisognerà di volta in volta però precisare (per gli insiemi, appunto, lo ripetiamo, il senso è che esiste una corrispondenza biunivoca, a priori non meglio identificata, tra A e B).

- Sostituendo al termine "funzione" quello di "morfismo", gli attributi precedenti si lasciano introdurre mediante un unico termine composto:
monomorfismo = morfismo iniettivo
epimorfismo = morfismo suriettivo
isomorfismo = morfismo biiettivo.
E' immediato allora comprendere il significato di affermazioni quali le seguenti: dato un qualsiasi morfismo f : A ® B, esso si può restringere in un epimorfismo di A sull'immagine di f in B; dato un qualsiasi monomorfismo f tra due insiemi A e B (o dell'insieme A nell'insieme B, o in B), esso si può restringere a un isomorfismo tra A e la sua immagine in B tramite f, ovvero a un isomorfismo di A su Im(f), o tra A e Im(f).
Inoltre, si parla di un endomorfismo di A quando si abbia a che fare con un morfismo f : A ® A , sicché sarà pure chiaro cosa saranno gli endomonomorfismi, o gli endoepimorfismi, di A, mentre si dice un automorfismo di A quello che altrimenti dovrebbe chiamarsi un endoisomorfismo. Tutto ciò fa sì che abbiano manifesto significato, comunque siano dati due insiemi A e B, gli insiemi Mono(A,B), Epi(A,B), Iso(A,B), tutti sottoinsiemi rilevanti di H(A,B), la cui effettiva "consistenza" assume un particolare significato. Per esempio, se Mono(A,B) non è vuoto, ecco che A si può considerare "più piccolo" di B, allo stesso modo che, se Epi(A,B) non è vuoto, B si può considerare "più piccolo" di A, tutte questioni alle quali dedicheremo speciale attenzione nel seguito. L'insieme degli endomorfismi di un dato insieme A, ovvero H(A,A), si designa più semplicemente con il simbolo H(A), ed ecco quindi, in virtù delle notazioni precedenti, un importante sottoinsieme di quest'ultimo insieme: Aut(A) Í H(A).

(I.23) Nota. Quelle precedenti sono alcune distinzioni notevoli sulla "natura" di una funzione, la cui introduzione mostra che, tranne casi "banali" (che riguardano l'insieme vuoto e i singleton) gli insiemi di funzioni non sono mai "democratici", allo stesso modo che non lo sono gli insieme delle parti P(A), se hanno almeno due elementi (e quindi basta in questo caso che A non sia vuoto).

- Comunque data una funzione f : A ® B, si può introdurre quel sottoinsieme di B costituito da tutti gli effettivi output degli elementi di A, ovvero di tutte le immagini tramite f degli elementi di A. Un tale sottoinsieme si chiama l'immagine di f, sinteticamente Im(f). Si suggerisce di evitare il pur frequente simbolo f(A), perché la notazione f(x) dovrebbe essere riservata ai soli elementi di A; f(A) sarebbe quindi una scrittura impropria, vedi anche quanto si dirà nel seguito, punto (I.30), sul corretto modo di scrivere l'immagine di un qualsiasi sottoinsieme di A, in particolare di A stesso, tramite un opportuno simbolo funzionale. Im(f) è un sottoinsieme di B, Im(f) Í B, così precisamente definito: Im(f) = {" b Î B ½ ($ a Î A : f(a) = b)}. [Si osservi bene che purtroppo, dovuto al già discusso particolare contesto della materia, è a volte usuale nei corsi di Analisi matematica parlare di codominio di una funzione in luogo di quella che è per noi invece soltanto l'immagine della funzione; il codominio è un insieme che va precisato all'inizio, quando viene assegnata la funzione (e chi sia può essere appunto scontato in Analisi), mentre l'immagine è un sottoinsieme del codominio che va determinato caso per caso.] Naturalmente, risulta Im(f) = B ses (abbreviazione frequente per: "se e soltanto se") f è suriettiva; se f non è suriettiva, ovvero se Im(f) Ì B, si può sempre restringere f a un'altra funzione, diciamola f', f' : A ® Im(f), tale che l'unica differenza tra f' e f sia quella relativa al codominio (quindi, una restrizione di codominio; su questo tipo di restrizioni, in generale non semplici, vedi quanto si dirà nell'appendice al presente capitolo), ovvero, resta identica la regola di derivazione (e con questo sono ben tre i termini usati come sinonimi in tale particolare contesto) input ® output: " x Î A Þ f'(x) = f(x). [A volte, per un abuso di notazione simile ad alcuni altri di cui si è già parlato, si indica questa f' con la stessa lettera f, ed f' si chiama ancora con lo stesso nome di f, commettendo in tale caso un abuso di linguaggio. Ripetiamo che tali abusi, che segnano il discrimine soggettivo tra pedanteria e rigore, sono in ogni caso soggetti alla responsabilità di chi li introduce, il quale dovrebbe in ogni caso essere capace di eliminarli, semmai sbuffando, dietro sollecitazione esterna.] Come dire che, a partire da una qualsiasi funzione f, che sia o no suriettiva, si può sempre immediatamente costruire una corrispondente funzione suriettiva la quale contiene sostanzialmente tutte le stesse informazioni fornite da f, sicché l'eventuale non suriettività di una funzione non è una "mancanza" significativa. Più rilevante risulta invece una sua eventuale non iniettività, alla quale non si può altrettanto facilmente ovviare (va da sé, qualora lo si desideri per qualche motivo). Si comprende comunque immediatamente che, in questo caso, bisognerà fare ricorso a restrizioni di dominio, alle quali allora accenniamo subito in generale, visto che si tratta di questione assai più semplice delle restrizioni di codominio, in un caso delle quali ci siamo già imbattuti. Comunque dati una funzione f : A ® B, e un sottoinsieme C Í A, è possibile costruire una nuova funzione g, che si dice la restrizione di f a C, g : C ® B, tale che, come prima, la regola della funzione resti immutata:
" x Î A Þ g(x) = f(x). Per una siffatta restrizione si utilizza a volte il simbolo f½C, che qualche volta resta semplicemente f, per un nuovo frequente abuso di notazione. L'operazione di restrizione in esame si può descrivere come una particolare funzione res : H(A,B) ® H(C,B) (la quale risulta, abbastanza chiaramente, suriettiva, tranne nel caso "banale": B = C = Æ, A ¹Æ, come si capirà meglio dopo aver letto il successivo punto (I.27); data una funzione da C a B, essa è infatti restrizione di tutte quelle funzioni da A a B che hanno il medesimo comportamento su C, mentre fuori si comportano in modo arbitrario). In modo del tutto analogo e semplice, si possono introdurre le estensioni di codominio (osserviamo che invece, le estensioni di dominio, come le restrizioni di codominio, sono argomento in generale più difficile), quando si abbia a che fare con una funzione f : A ® B il cui codominio B sia un sottoinsieme di un altro insieme C, vale a dire B Í C. La funzione estesa di f è naturalmente quella funzione h : A ® C della quale la regola sia sempre la stessa di f,
" x Î A Þ h(x) = f(x). Anche nel caso di una siffatta estensione, si utilizza a volte il medesimo simbolo f. L'operazione di estensione in esame si può descrivere come una particolare funzione ext : H(A,B) ® H(A,C), e come era chiaro che res è suriettiva, così è forse ancora più chiaro che ext è iniettiva (funzioni distinte f, g da A a B, tali cioè che $ a Î A ½ f(a) ¹ g(a), restano ovviamente ipso facto distinte come funzioni da A a C, in quanto f(a) ¹ g(a) significa sempre la stessa cosa, tanto in B quanto in C). Naturalmente, sia res che ext sono simboli compatti che non esprimono completamente la situazione a cui sono collegati, vale a dire il fatto che l'insieme C si trovi nelle condizioni atte a giustificare l'introduzione di questi due particolari morfismi.

[Si rifletta: res è in generale iniettiva? Ed ext è in generale suriettiva?]

(I.24) - Comunque data una funzione f : A ® B, si può introdurre una funzione pull-back che procede in senso inverso rispetto ad f, ma ha come codominio l'insieme delle parti P(A) anziché A. La denoteremo con il simbolo f°, ed è la funzione f° : B ® P(A) che associa ad ogni elemento b di B il sottoinsieme di A costituito da tutti quegli input che hanno come output esattamente b (essi si dicono le immagini inverse, o controimmagini, o antiimmagini, di b, sicché f° viene chiamata anche talora la funzione inversa di f, con il rischio però di confonderla con un'altra funzione inversa, una denominazione molto più appropriata, di cui presto diremo). In simboli logici:
f°(b) = {" a Î A ½ f(a) = b} Î P(A).
Naturalmente, f° (b) = Æ ses b Ï Im(f).

Un'operazione fondamentale

Tutte le volte che si hanno una funzione f : A ® B, e una funzione g : B ® C, cioè tali che: codom(f) = dom(g), ovvero, tutte le volte che si hanno un collegamento f tra A e B, e un collegamento g tra B e C, è possibile introdurre un collegamento diretto tra A e C, mediante una nuova funzione: h : A ® C (a sua volta "funzione" di f e g), che resta così definita: " x Î A, h(x) = g(f(x)) .
Si noti bene che, per ipotesi, f(x) Î B, e che B è il dominio di g, sicché l'espressione g(f(x)) ha un significato univoco. La funzione h si dice la funzione composta di f tramite g, o anche il prodotto di g per f (ma pure prodotto di composizione, o prodotto operatorio, o anche composizione di g per f), per il quale prodotto si usa un simbolo speciale: "o", ovvero si pone h = gof (qualche volta al posto del "tondino" si usa il "punto", e qualche volta proprio niente: ci si limita a scrivere di seguito gf; non si confonda ovviamente questo segno speciale o con il tondino in alto che è stato precedentemente utilizzato nel punto (I.24), per definire il pull-back di una funzione). Si noti bene l'inversione che ne risulta tra f e g, la quale consegue dal fatto che il simbolo di funzione si scrive d'ordinario a sinistra del simbolo di variabile, sicché si vuole per esempio riscrivere l'identità definitoria precedente nella forma, mnemonicamente assai comoda: (gof)(x) = g(f(x)) (si noti bene che la prima coppia di parentesi rotonde, in (gof), ha un significato del tutto diverso dalla seconda coppia di parentesi, in f(x)). Per ovviare a tale comunque fastidiosa occorrenza, c'è chi suggerisce di porre i simboli funzionali a destra delle variabili, e scrivere quindi qualcosa del tipo xf in luogo di f(x) (con in più un'eliminazione di parentesi in fondo non strettamente necessarie; si può ben scrivere per esempio cosx in luogo di cos(x)), di modo che l'applicazione ripetuta di f e g, nell'ordine, verrebbe scritta come (xf)g = x(fog). Allo stesso scopo risponde pure una proposta notazione esponenziale, di uso non rarissimo, secondo la quale si dovrebbe scrivere xf in luogo di f(x), sicché risulterebbe (xf)g = xfg (e qui si è addirittura soppresso anche quel "tondino" simbolo di prodotto tra funzioni). Tutto considerato, noi preferiamo però restare aderenti a una consolidata tradizione simbolica, seppur essa costringe a qualche attenzione, ed eliminare "poco", al fine di evitare fraintendimenti.
Si può sottolineare immediatamente che il precedente prodotto gode ovviamente della proprietà associativa (la stessa di cui godono unione e intersezione tra insiemi, o le ordinarie operazioni di somma e prodotto tra numeri naturali, o anche tra numeri reali, per chi conosce davvero tali operazioni; trattare invece di operazioni non associative è cosa assai delicata, e noi non ne incontreremo mai, o quasi):

(I.25) " f Î H(A,B) , " g Î H(B,C), " h Î H(C,D) Þ ho(gof) = (hog)of .

La relativa "dimostrazione" è un semplice esercizio di "calligrafia", un accurato shifting di parentesi, proprio quelle parentesi che la proprietà associativa consente in molti casi, ancorché solo a posteriori, di eliminare:
" x Î A, (ho(gof))(x) = h((gof)(x)) = h((g(f(x))),
e l'identico risultato si ottiene a partire dalla funzione (hog)of:
((hog)of)(x) = (hog)(f(x)) = h((g(f(x))), cvd o qed (abbreviazioni usuali rispettivamente per "come volevasi dimostrare", o per "quod erat demonstrandum").

(La facile dimostrazione risulta in realtà completa soltanto quando si noti che le a priori due diverse funzioni che si mettono a confronto hanno in ogni caso il medesimo dominio e il medesimo codominio).

Non c'è bisogno di speciali considerazioni per persuaderci poi del fatto che il precedente prodotto è in generale non commutativo. A parte il fatto che quando si può costruire gof spesso non è possibile costruire fog, anche nel caso che entrambe le funzioni restino definite, e siano "confrontabili", ovvero che abbiano lo stesso dominio e codominio, ci si deve aspettare che in generale risulti: (gof)(x) ¹ (fog)(x), ovviamente per qualche elemento x nel comune dominio delle due funzioni.

(In relazione a quanto precede, ci si può domandare: quando è possibile costruire entrambe le funzioni gof e fog? Posto A = dom(f), B = cod(f), con abbreviazione naturale rispetto a codom, perché si possa costruire gof deve intanto risultare, come abbiamo visto: B = cod(f) = dom(g). Detto, come prima, C il codominio di g, l'esistenza della fog implica analogamente: cod del secondo fattore = cod(g) = dom del primo fattore = dom(f), ossia C = A. Insomma, il "doppio" prodotto di nostro interesse si può effettuare soltanto nel caso illustrato dalla seguente figura:  , una situazione che peraltro incontreremo spesso, talora pure nel caso particolare A = B, vale dire quando f e g sono endomorfismi di un dato insieme A. Ciò premesso, è chiaro che, nel contesto che stiamo analizzando, risulta gof Î H(A), mentre fog Î H(B), sicché le due funzioni prodotto sono confrontabili ses A = B; vale a dire, dell'eventuale identità (gof)(x) = (fog)(x) ha senso occuparsi soltanto quando f, g siano endomorfismi di uno stesso insieme A, ma sulla questione ritorneremo).

E' pure facile persuadersi infine che sussiste il seguente:

(I.26) Teorema. Il prodotto di due monomorfismi è un monomorfismo; il prodotto di due epimorfismi è un epimorfismo; quindi, il prodotto di due isomorfismi è un isomorfismo.

Alcune funzioni ragguardevoli

(I.27) - Tutte le volte che si hanno due insiemi A, B, uno contenuto nell'altro, per esempio A Í B, si può introdurre una funzione speciale i(A,B): A ® B, che si chiama l'inclusione di A in B, ed è semplicemente la funzione che associa ad ogni elemento x Î A lo stesso elemento x Î B: i(A,B)(x) = x (per i(A,B) si utilizza un simbolo speciale,  , sicché quando uno vede scritto A  B , senza ulteriori specificazioni, viene simultaneamente informato del fatto che gli si dà una ben precisa funzione, e che A è contenuto in B. Ovviamente i(A,B) risulta un monomorfismo, ed Im(i(A,B)) è uguale ad A. Nel caso particolare A = B, in luogo di i(A,A) si può scrivere semplicemente iA, o meglio idA, che mette migliore enfasi sulla circostanza che questa funzione si chiama, come è naturale, la funzione identità di A. Informiamo che è opportuno introdurre la convenzione che quanto precede abbia significato anche nell'eventualità in cui A sia l'insieme vuoto, nel qual caso si dà senso, per ogni insieme X, ai simboli i(Æ,X), con riferimento all'inclusione Æ Í X, e al simbolo idÆ! (Naturalmente, i(Æ,X) si dirà un monomorfismo, il quale sarà anche un epimorfismo ses pure X = Æ, ossia ses i(Æ,X) = idÆ, convenzioni perfettamente in regola con tutte quelle introdotte in precedenza). Si tratta di "funzioni" (si direbbe forse meglio, di "simboli funzionali") che non richiedono alcuna specificazione in ordine alla regola di associazione input-output, visto che non esistono input, ma soltanto in ordine a loro dominio e codominio. Risulta in ogni caso, qualsiasi sia l'insieme X: H(Æ,X) = {i(Æ,X)}, e in particolare H(Æ) = Aut(Æ) = {idÆ}. E visto che ci siamo, si può per completezza aggiungere che H(A,Æ) deve sempre considerarsi uguale al vuoto, qualunque sia A ¹ Æ, perché se esiste qualche input a Î A, ad esso deve potersi associare un output nel codominio della funzione, e se questo codominio è vuoto ecco che non può esistere alcuna funzione da A al vuoto.

Notiamo subito che, con riferimento all'operazione di prodotto tra funzioni, e ricordando i due morfismi res ed ext, risultano sussistere le seguenti identità:

" C Í A, " f Î H(A,B) Þ foi(C,A) = f½A = res(f) ;
" C Ê B, " f Î H(A,B) Þ i(B,C)of = ext(f) ;
foidB = f ; idCof = f

(a proposito delle ultime due identità, si noti che la funzione f può essere moltiplicata a destra per idB, ma non a sinistra, mentre può essere moltiplicata a sinistra per idC, ma non a destra, naturalmente a meno che non risulti B = C).

(I.28) - Per ogni insieme A non vuoto, si può introdurre una rappresentazione (che diremo naturale, o canonica, vedi in seguito) di A in P(A), rA : A ® P(A), la cui esistenza dimostra che l'insieme delle parti P(A) è sicuramente "maggiore o uguale" di A, in quanto rA risulta una funzione iniettiva; al posto del termine iniettiva, e associato a rappresentazione, si utilizza spesso, con linguaggio assai espressivo, fedele (una rappresentazione fedele non cancella alcuna distinzione tra gli elementi di A, i quali mantengono la loro "identità" nella sede della rappresentazione, nel presente caso P(A)). Una rappresentazione fedele di un insieme in un altro è ovviamente un isomorfismo dell'insieme dato sulla sua immagine nell'altro insieme. La rappresentazione di cui si sta parlando è semplicemente la seguente "banale" funzione:

                                         rA : A       ®          P(A)
aÎA          {a} Î P(A)

(nel caso particolare A = Æ, si può ancora introdurre rÆ, e risulta: rÆ = i(Æ,P(Æ))).

Domanda: rA può mai essere suriettiva, per qualche particolare scelta di A?

(I.29) - Un'altra naturale (e banale) rappresentazione fedele di un insieme A, dato un altro qualsiasi insieme B non vuoto che funga da supporto, è la seguente: cB : A ® H(B,A), che associa ad ogni elemento a Î A la funzione costante da B ad A così definita: " x Î B, (cB(a))(b) = a (cB(a) è la funzione da B ad A che resta associata ad A tramite la rappresentazione in discorso). E' necessario che B sia scelto non vuoto, perché altrimenti H(Æ,A) è un singleton, e non può essere sede di alcuna rappresentazione fedele di A (a meno che, naturalmente, A non sia esso stesso il vuoto, oppure un singleton; si tratta di "casi limite" sui quali non conviene perdere troppo tempo, e soprattutto affaticare la memoria per ricordarne a priori la "soluzione", anche se la riflessione su di essi può talvolta costituire un utile esercizio).

Domanda: cB può mai essere suriettiva, per qualche particolare scelta degli insiemi A e B?

(I.30) - Comunque data una funzione f : A ® B, si possono associare ad essa due nuove importanti funzioni:
f* : P(A) ® P(B) (detta push-down, o "immagine diretta");
f* : P(B) ® P(A) (detta ancora pull-back, o "immagine inversa"),
definite rispettivamente mediante le regole:

" S Î P(A) Þ f*(S) = Im(f½S) = {" y Î B ½ ($ s Î S : f(s) = y)}
(f*(S) è cioè l'insieme delle immagini in B di tutti gli elementi di S)

" T Î P(B) Þ f*(T) = Im(f°½T) = {" x Î A ½ f(x) Î T}
(f*(T) è cioè l'insieme delle immagini inverse in A di tutti gli elementi di T).

[La scelta degli asterischi in alto e in basso corrisponde a una ben precisa e diffusa convenzione, quando si tratta di associare un qualche morfismo f' a un morfismo f : X ® Y, del quale vengano opportunamente modificati dominio e codominio, diciamo da X a X' e da Y a Y'. Se f' va nello stesso verso di f, e quindi da X' a Y', ecco che si usa l'asterisco in basso (si dice che il passaggio dalla terna X, Y, f alla terna X', Y', f' è covariante); se f' va in senso inverso, e quindi da Y' a X', ecco che si usa l'asterisco in alto (e si dice che il il passaggio dalla terna X, Y, f alla terna X', Y', f' è controvariante). Nel caso attuale, ovviamente, X = A, Y = B, A' = P(A), B' = P(B).]

Si noti che adesso ha senso l'identità f*(A) = Im(f) (e non Im(f) = f(A)), mentre ovviamente f*(B) = A. Scrivere f(A) = Im(f) significa confondere f con f*, cosa che non è opportuna (possono permettersi siffatti abusi di notazione i più esperti, che sanno in caso come uscirne fuori). Inoltre che, ovviamente:
(idA)* = idP(A) = (idA)*, e che f* risulta evidentemente collegata alla funzione f° dianzi definita, oltre che dalla definizione stessa, dalla seguente "ovvia" identità: " b Î B Þ f*({b}) = f°(b) (la quale si può anche esprimere, ricordando la rappresentazione canonica rB : B ® P(B), mediante l'identità: f*orB = f°). Si tratta qui soltanto di fare attenzione a chi sono (dove sono) gli input delle diverse funzioni in gioco.
Ancora, se A Í B, e se f = i(A,B), risulta P(A) Í P(B), e poi:
f* = (i(A,B))* = (i(P(A),P(B)))* ; " X Î P(B) Þ (i(A,B))*(X) = XÇA .

Concludiamo questo punto elencando alcune proprietà interessanti (ciascuna di agevole dimostrazione) che riguardano la coppia di funzioni "gemelle" f* e f*, che diremo in qualche modo "derivate" dalla (o della) funzione f (rispettivamente covariante e controvariante). Sono relazioni che non si chiede di imparare a memoria; basta sapere che esse esistono, comprenderne il senso quando le si osservano, e far loro eventuale ricorso quando sia conveniente utilizzarle per qualche dimostrazione.

(I.30I) " S, S' Î P(A), S Í S' Þ f*(S) Í f*(S') ;

(I.30II) " T, T' Î P(B), T Í T' Þ f*(T) Í f*(T')

(i due precedenti piccoli "teoremi" si esprimono a parole con il dire che tanto f* quanto f* "mantengono", o "conservano", o "preservano", o "rispettano", la relazione di inclusione definita nei loro rispettivi domini);

(I.30III) " S, S' Î P(A) Þ f*(SÈS') = f*(S)Èf*(S') ;

(I.30IV) " T, T' Î P(B) Þ f*(TÈT') = f*(T)È f*(T') ;

(I.30V) " S, S' Î P(A) Þ f*(SÇS') Í f*(S)Çf*(S')

(a proposito della(I.30V). si noti per esempio che può darsi il caso di due sottoinsiemi S, S' non vuoti e disgiunti di un insieme A, tali che:
f*(S) = f*(S') = Im(f), sicché f*(SÇS') = f*(Æ) = Æ, mentre:
f*(S)Çf*(S') = Im(f));

(I.30VI) " T, T' Î P(B) Þ f*(TÇT') = f*(T)Çf*(T')

(ovvero, f* e f* mantengono, o "sono compatibili con", o "sono coerenti con", etc., le operazioni di unione definite nei loro rispettivi domini; altrettanto può dirsi per f* rispetto alla corrispondente operazione di intersezione, mentre in questo caso è anomalo, al solito "in generale", il comportamento di f*);

(I.30VII) " S Î P(A) Þ f*(CA(S)) Ê CIm(f)(f*(A))

(I.30VIII) " T Î P(B) Þ f*(CB(T)) = CA(f*(T))

(I.30IX) " S, S' Î P(A) Þ f*(S-S') Ê f*(S)-f*(S') ;

(I.30X) " T, T' Î P(B) Þ f*(T-T') = f*(T)-f*(T')

(le precedenti quattro relazioni mostrano ancora una volta il carattere anomalo, in generale, di f* rispetto a quello di f*; si può aggiungere che nelle (I.30VII) e (I.30VIII) vale il segno di uguaglianza se, e soltanto se, la funzione f è iniettiva);

(I.30XI) " f Î H(A,B) , " g Î H(B,C) Þ (gof)* = g*of* ;

(I.30XII) " f Î H(A,B) , " g Î H(B,C) Þ (gof)* = f*og*

(si noti nella precedente identità l'inversione tra i due "fattori" f e g, peraltro assolutamente necessaria a priori onde consentire la composizione delle funzioni in gioco);

(I.30XIII) " S Î P(A) Þ f*(f*(S)) Ê S

(dopo lo studio del successivo punto dedicato a "Funzioni e partizioni", si comprenderà bene come f*(f*(S)) coincida con l'unione di tutti i blocchi della partizione associata a f che intersecano S, ovvero che non sono disgiunti da S, e che l'insieme f*(f*(S)) si può definire quindi la saturazione di S rispetto alla partizione in oggetto; ne consegue, banalmente, che nella (I.30XIII) vale il segno di uguaglianza, per ogni elemento S, se f è iniettiva);

(I.30XIV) " T Î P(B) Þ f*(f*(T)) Í T

(anche questa relazione è talora "migliorabile" con il segno di uguale, per esempio se T Í Im(f), con la conseguenza che in essa vale l'uguaglianza per ogni elemento T se f è suriettiva; in generale, invece, f*(T) = f*(TÇIm(f)), e
f*(f*(T)) = f*(f*((TÇIm(f))) = TÇ(Im(f)) Í T, appunto).

Caratterizzazioni algebriche della "qualità" di un morfismo

In questa sezione proveremo come sia possibile caratterizzare i monomorfismi e gli epimorfismi (e quindi naturalmente anche gli isomorfismi) mediante loro proprietà fondamentali rispetto al prodotto di composizione con altri morfismi, ovvero, dal punto di vista della struttura algebrica della totalità dei morfismi.

(I.31) Teorema. Siano A, B due insiemi arbitrari, e sia f : A ® B un qualsiasi morfismo da A verso B. Se $ g Î H(B,A) ½ gof = idA, allora f è di necessità un monomorfismo.

(Nelle precedenti condizioni, si dice che f è invertibile a sinistra, perché il morfismo g di cui si è supposta l'esistenza figura alla sinistra di f, e il teorema (I.31) si può anche enunciare affermando che i morfismi in H(A,B) i quali siano invertibili a sinistra sono necessariamente contenuti in Mono(A,B)).

Dim. Si supponga per assurdo che f non sia un monomorfismo, ovvero che esistano due elementi x, y Î A, con x ¹ y, tali che sia f(x) = f(y). Allora, applicando a questa identità la funzione g, si ottiene g(f(x)) = g(f(y)) (per l'unicità di un output fissato un input), e da questa, per definizione di prodotto operatorio, (gof)(x) = (gof)(y). Ma per ipotesi gof = idA, sicché (gof)(x) = x e (gof)(y) = y, e quindi x = y, che contraddice l'assunzione x ¹ y, cvd. ä

(I.32) Teorema. Siano A, B due insiemi arbitrari, e sia f : A ® B un qualsiasi morfismo da A verso B. Se $ h Î H(B,A) ½ foh = idB, allora f è di necessità un epimorfismo.

(Nelle precedenti condizioni, si dice che f è invertibile a destra, perché il morfismo h di cui si è supposta l'esistenza figura adesso alla destra di f, e il teorema (I.32) si può anche enunciare affermando che i morfismi in H(A,B) i quali siano invertibili a destra sono necessariamente contenuti in Epi(A,B)).

Dim. La dimostrazione è facilissima, perché, " z Î B, si ha:
foh = idB Þ (foh)(z) = f(h(z)) = idB(z) = z,
ed ecco subito quindi un elemento x = h(z) Î A tale che f(x) = z, che è proprio la condizione di suriettività della funzione f. ä

(I.33) Corollario. Ogni inverso sinistro di un monomorfismo è un epimorfismo, allo stesso modo che ogni inverso destro di un epimorfismo è un monomorfismo.

(I.34) Corollario. Siano A, B due insiemi arbitrari, e sia f : A ® B un qualsiasi morfismo da A verso B. Se f è invertibile tanto a destra quanto a sinistra, in una sola parola, se f è invertibile, allora f è un isomorfismo.

L'ultima affermazione del corollario (I.34) si può ulteriormente, e facilmente, precisare:

(I.35) Teorema. Viceversa, se f è un isomorfismo, allora f è invertibile.

Dim. In effetti, se f è un isomorfismo tra A e B, la funzione g : B ® A, che associa ad ogni output in B l'unico input in A da cui essa proviene, ossia:
f-1(b) = a Û f(a) = b, è manifestamente tale che gof = idA, fog = idB . ä

Alla funzione g di cui alla dimostrazione precedente, costruita in modo evidentemente dipendente da f, si dà il nome di inversa di g, e si indica con il simbolo f-1. E' chiaro che f-1 è un isomorfismo al pari di f, e che:

(I.36)  (f-1)-1 = f

(la (I.36) esprime l'involutorietà dell'operazione di passaggio alla funzione inversa - si rammenti (I.17)).

Notiamo bene che non solo un isomorfismo risulta invertibile tanto a destra quanto a sinistra, ma che esiste un morfismo che realizza simultaneamente entrambe tali, a priori distinte, condizioni di invertibilità, del quale si parla allora anche come di un inverso bilaterale, o bilatero.
Data la natura degli enti in esame, è pure chiaro che, se con f continuiamo a indicare un isomorfismo tra A e B, la precedente funzione f-1 è l'unica che possa fungere da inversa della funzione f, tanto a destra quanto a sinistra, nel senso che, nelle attuali ipotesi, risulta: gof = idA Þ g = f-1 ; mentre analogamente:
foh = idB Þ g = f-1 . Raccogliamo in modo esplicito il risultato:

(I.37) Teorema (Unicità dell'inverso algebrico) - Se A, B sono due insiemi qualsiasi, e se f : A ® B è un isomorfismo qualsiasi, f ammette un'unica inversa sinistra e un'unica inversa destra, entrambe coincidenti nell'isomorfismo
f-1 : B ® A dianzi definito.

Dim. Come abbiamo detto, si tratta solo di esprimere una manifesta verità di fatto, per la quale non c'è bisogno di alcuna dimostrazione. Pure, riteniamo possa essere istruttivo, a fini di successivi ulteriori sviluppi del medesimo tipo di considerazioni, provare come si possa dimostrare l'asserto in un modo del tutto "formale", che utilizzi soltanto l'esistenza del prodotto di composizione, e la sua associatività. Si assumano prima di tutto, per qualche morfismo f in un qualche insieme di funzioni H(A,B), le identità gof = idA, foh = idB, per certi morfismi g, h Î H(B,A), e si cominci con il provare che di necessità g = h. In effetti, moltiplicando per esempio la prima identità a destra per h, si avrà: (gof)oh = idAoh = h, e usando la proprietà associativa nel primo termine si avrà: (gof)oh = go(foh) = goidB, = g, e quindi in definitiva h = g. ä

(I.38) Nota. Possiamo aggiungere poi che, risultando manifestamente il prodotto fog (quando sia possibile effettuarlo) di due isomorfismi f e g ancora un isomorfismo, sussiste la seguente "regola" per la formazione dell'isomorfismo inverso di fog: (fog)-1 = (g-1)o(f-1), un'identità che è facilissimo dimostrare (basta verificare che la funzione che appare nel RHS della predetta identità funge da inversa, tanto destra quanto sinistra, per fog, circostanza che, ancora una volta, è una diretta conseguenza della proprietà associativa del prodotto operatorio).

(I.39) Nota. Un altro modo di concepire l'isomorfismo inverso f-1 di un isomorfismo f, è di notare che esso non è altro che il morfismo che si ottiene dalla funzione reciproca di f, la f° di cui al punto (I.24), mediante la attualmente possibile restrizione di codominio inerente alla rappresentazione rA : A ® P(A) (punto (I.28)). Si noti bene però che, mentre per ogni f si può introdurre la f°, sarà invece lecito usare il simbolo f-1 solo quando f sia un isomorfismo, neppure quando sia un monomorfismo (se non attraverso un abuso di notazione), e che nel caso di un isomorfismo, seppure molto "vicine" tra loro, f-1 e f° non andrebbero comunque mai confuse.

I due teoremi (I.31) e (I.32) si possono in un certo senso invertire, ammettono cioè un viceversa, anche se condizionato il primo, e di tipo assai particolare, come vedremo, il secondo. Prima però di procedere con i relativi enunciati, sarà bene che lo studente si familiarizzi con immagini mentali e generali relative ai monomorfismi e agli epimorfismi. Ecco un tipico monomorfismo f da A in B, cioè un isomorfismo di A su un sottoinsieme C di B, il quale coincide con l'immagine di f, ed f risulta il prodotto dell'inclusione canonica i(C,A) con un isomorfismo in H(A,C), ottenuto da f per restrizione sul codominio (è questo manifestamente un caso particolare del "teorema di decomposizione" che vedremo in seguito, punto (I.47)):

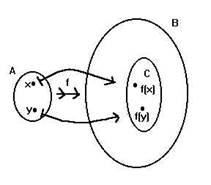
(Fig. I.40)

ed ecco invece un tipico epimorfismo f da A su B, rappresentato A come un quadrato, B come un suo lato, ed f come la proiezione del quadrato sul lato:

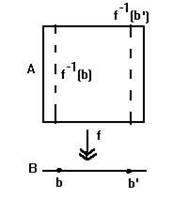
(Fig. I.41)

In questa seconda immagine, si cerchi di visualizzare la partizione associata ad f (vedi il punto successivo "Funzioni e partizioni"), i cui blocchi f-1(b), al variare di b Î B, sono dei segmenti verticali, dei quali si parla anche, con terminologia suggestiva, come delle fibre della proiezione f.

Ciò premesso, si comprende subito dalle figure come sia facile invertire a sinistra un monomorfismo, a priori in tanti modi diversi (il che esprime la generale non unicità di un inverso sinistro di un monomorfismo), costruendo una funzione g da B verso A, la quale mandi tutto ciò che è fuori di C "a caso" in qualche elemento di A, mentre ad ogni elemento di C associa esattamente quell'unico elemento a Î A di cui esso è l'immagine:

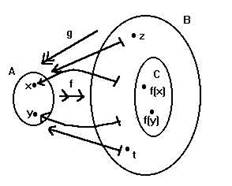
(Fig. I.42)
(Rappresentazione di un inverso sinistro del monomorfismo f)

Analogamente, per costruire un inverso destro (anch'esso manifestamente non unico in generale) dell'epimorfismo descritto nella Fig. I.6, basta pensare a una funzione h : B ® A tale che, per " b Î B, risulti h(b) Î f-1(b), una determinazione che appare possibile in quanto f-1(b) è per ipotesi non vuoto:

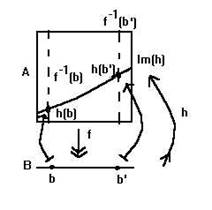
(Fig. I.43)
(Rappresentazione di un inverso destro dell'epimorfismo f)

Un inverso destro di una suriezione f si chiama anche una sezione di f, con parola che è chiaramente allusiva alla proprietà del sottoinsieme immagine della sezione, che appunto uniseca ciascuna fibra di f. Corrispondentemente, un inverso sinistro di una iniezione f si chiama allora una cosezione di f, ma c'è anche l'uso di chiamare quest'ultimo una retrazione di f (le retrazioni continue sono particolarmente importanti in topologia), e di conseguenza qualificare invece una sezione con il termine coretrazione. Ovviamente, (I.31) e (I.32) implicano che le sezioni sono monomorfismi, e le cosezioni epimorfismi.

(Si noti anche che nel primo caso non appare chiaramente possibile costruire un morfismo g da B verso A il quale realizzi la condizione di invertibilità destra, ovvero fog = idB, mentre nel secondo non appare chiaramente possibile costruire un morfismo h da B verso A il quale realizzi la condizione di invertibilità sinistra, ovvero hof = idA - si noti bene, naturalmente, il modo con cui si scambiano i ruoli, in tutte le precedenti identità, dominio e codominio).

Dopo queste premesse euristiche (che riguardano cioè la fase della "ricerca" della verità - la parola greca corrisponde naturalmente al celebre eureka di Archimede), enunciamo precisamente gli annunciati teoremi che invertono rispettivamente (I.31) e (I.32).

(I.31') Teorema. Siano A, B due insiemi arbitrari, e sia f : A  B un qualsiasi monomorfismo da A verso B. Se A è diverso dal vuoto, allora f è invertibile a sinistra, mentre se A = Æ, e B ¹Æ, f (che coincide allora con il morfismo di inclusione i(Æ,B)) non può essere invertibile a sinistra. Infine, nel caso
A = B = Æ, risulta f = idÆ, ed f è manifestamente invertibile tanto a sinistra quanto a destra (dal momento che, banalmente, in virtù delle convenzioni fissate per il simbolo, risulta: idÆoidÆ = idÆ).

Dim. A questo punto potremmo considerarla del tutto ovvia. ä

(I.32') Teorema. Siano A, B due insiemi arbitrari, e sia f : A  B un qualsiasi epimorfismo da A verso B. Allora f è sempre invertibile a destra.

Dim. Come si fa a "dimostrare" il pure "ovvio" teorema in oggetto? Su cosa di "più semplice" ci si può poggiare per dedurre la conclusione desiderata, che nel caso degli insiemi finiti (compreso il caso B = Æ, perché allora pure A = Æ ed f risulta l'identità del vuoto; viceversa, se A = Æ, anche B deve essere vuoto, dal momento che f è supposta suriettiva) appare <<luminosamente autoevidente>>? Si "vede" infatti chiaramente che basta scegliere, elemento per elemento in B, un elemento "a caso" nella corrispondente fibra f-1(b) Í A, con qualche problema "filosofico" appunto quando B sia infinito. Ecco perché il teorema (I.32') viene considerato in realtà un assioma, un principio della teoria degli insiemi, che si denomina, per chiari motivi, assioma della scelta, o anche assioma di Zermelo, dal nome del matematico tedesco Ernst Zermelo (1871-1956), che per primo lo studiò sistematicamente. ä

(Sulla questione torneremo in appendice al capitolo III, a proposito di un equivalente "assioma di buon ordinamento".)

Chiudiamo questa sezione notando che, mentre quella di prodotto operatorio nella totalità di tutti i morfismi è una struttura algebrica che può dirsi solo parziale, in quanto non sempre due morfismi si possono comporre tra di loro, al contrario, per ogni insieme A, l'insieme degli endomorfismi H(A) gode della proprietà che è sempre possibile fare il prodotto di due suoi elementi di H(A). Inoltre, che H(A) risulta chiuso rispetto all'operazione di prodotto operatorio, nel senso che: la composizione di due endomorfismi è ancora un endomorfismo, e quindi è ancora un elemento di H(A) (allo stesso modo che chiusi rispetto a tale operazione risultano pure i suoi sottoinsiemi Mono(A), Epi(A), e Aut(A), tutti e tre non vuoti in quanto contenenti almeno idA). Si tratta del prototipo importante di quella che diremo una struttura algebrica, un insieme cioè dotato di una certa operazione tra "coppie" (ordinate) di propri elementi, un concetto al quale dedicheremo particolare attenzione nel capitolo VI. Per ora basterà anticipare che a una struttura quale H(A) riserveremo la denominazione, non universalmente condivisa, di semigruppo (c'è chi parla infatti di gruppoide, o in questo caso speciale, come subito diremo dotato di unità, monoide) con tale termine riferendoci alla sola validità della proprietà associativa del prodotto operatorio. Ad esso aggiungeremo la specificazione unitario, in quanto H(A) possiede pure un elemento che moltiplicato per ciascun altro, a destra o a sinistra, lo lascia invariato. E' facile convincersi che un elemento con siffatte proprietà (plurale, perché sono due) è certamente idA, e che se un tale elemento esiste in un qualsiasi semigruppo (la cui operazione di prodotto indicheremo per il momento con il simbolo generico *, che comprende come caso particolare il prodotto operatorio "tondino"), ovvero se il semigruppo è come abbiamo detto unitario, allora esso è pure unico, sicché sarà lecito parlare, con l'articolo determinativo, della unità del semigruppo, o identità, o elemento neutro, o perfino semplicemente "1". Infatti, se u è, tanto per fissare una notazione, un siffatto elemento, avente la proprietà cioè che per ogni elemento x del semigruppo risultano valide entrambe le identità x*u = x, u*x = x, e se v fosse un altro elemento godente della medesima proprietà, ossia x*v = x, v*x = x, ecco che se ne dedurrebbe immediatamente, ponendo per esempio x = v nella prima delle quattro, v *u = v, mentre ponendo x = u nell'ultima delle quattro, si dedurrebbe v*u = u, sicchè in definitiva v *u = v = u, e quindi v = u, cvd.

Si tratta di un primo facile teorema di teoria dei semigruppi (teorema di unicità dell'eventuale elemento neutro), che permette di chiamare idA l'identità non solo dell'insieme A, ma anche del semigruppo H(A). Non solo, ma si tratta di un elemento neutro anche per i sottosemigruppi di H(A) che abbiamo sopra menzionato, vale a dire Mono(A), Epi(A), e Aut(A). Sono naturalmente tutti concetti sui quali torneremo con cura, per ora basterà soltanto, allo scopo di introdurre un po' di "linguaggio" specifico dell'Algebra, che il semigruppo unitario Aut(A) risulta speciale rispetto agli altri, in quanto, oltre ad associatività (indispensabile) ed esistenza di una unità per la sua operazione, esso gode anche della addizionale proprietà che ogni suo elemento risulta invertibile, tanto a destra quanto a sinistra, nel senso che, per ogni elemento, diciamolo ancora x per uniformità con il caso generale, in Aut(A), esiste un elemento y (che abbiamo già visto sostanzialmente essere addirittura unico, quando esistente, teorema di unicità dell'eventuale inverso bilatero, vedi (I.37), ma, si noti bene, non di un inverso solo destro o solo sinistro) tale che x*y = u, y*x = u. Semigruppi unitari soddisfacenti tale ulteriore condizione di invertibilità (tout court) si diranno gruppi, ed ecco che abbiamo visto così, sia pure per sommi capi, come la teoria degli insiemi fornisca un'enorme "famiglia" di esempi, di semigruppi e di gruppi...

Funzioni e partizioni

Studiamo adesso, assegnato un qualsiasi insieme non vuoto A, l'insieme delle partizioni di A, che indicheremo con il simbolo PT(A), e che risulta manifestamente un sottoinsieme proprio dell'insieme delle parti dell'insieme delle parti di A, ovvero: PT(A) Ì P(P(A)). Si rammenti che una singola partizione P è un insieme di sottoinsiemi di A, vale a dire un sottoinsieme, peraltro proprio, di P(A): P Ì P(A) Û P Î P(P(A)). Orbene, per ogni insieme B, PT(A) è sede di un'importantissima rappresentazione, diciamola P (una scelta abbastanza scontata), ma in generale non fedele, dell'insieme dei morfismi H(A,B):
P : H(A,B) ® PT(A).

P (e avremmo dovuto scrivere PH(A,B), oppure P(A,B), con simbolismo però in entrambi i casi troppo "pesante", e inutile, almeno fino a quando A e B restino fissati) associa ad ogni funzione f Î H(A,B) una partizione P(f) di A, che si può indicare anche con il simbolo Pf, i cui blocchi sono così ovviamente definiti: il blocco che contiene un dato elemento a Î A, e che è tradizionale indicare con [a], senza alcun riferimento esplicito alla funzione f, è l'insieme di tutti gli elementi x Î A tali che f(x) = f(a). In altre parole, tenuto conto della (I.24), si può dire che: [a] = f°(f(a)) Î P(A), o anche: P(f) = Pf = Im(f°of).
Dovrebbe essere immediatamente chiaro che questi blocchi sono di fatto gli elementi di una partizione di A. Ciascuno di essi non è vuoto per definizione, ancora per definizione la loro unione è l'intero A. Per quanto riguarda la proprietà di disgiunzione, se due blocchi, a priori diversi, [a] e [a'], per certi elementi a, a' Î A, hanno un'intersezione non vuota, cioè se [a]Ç[a'] ¹ Æ, allora $ x Î A½ x Î [a]Ç[a'], e quindi da un canto f(x) = f(a), dall'altro f(x) = f(a'), sicché f(a) = f(a'). Ne consegue che, " y Î [a], risulta f(y) = f(a) = f(a') Þ y Î [a'], così come inversamente, " y Î [a'], risulta f(y) = f(a') = f(a) Þ y Î [a], e in definitiva [a] = [a'] = [x], cvd.
Nella figura seguente si è cercato di rappresentare la tripartizione associata a una funzione f tra due insiemi A e B che ha un'immagine in B costituita da tre soli elementi x, y, z Î B, i quali sono immagine dei tre blocchi X, Y, Z Ì A (ossia, X, Y, Z Î P(A)):

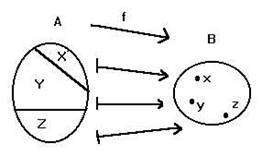
(Fig. I.44)

[Si noti che, perché quanto precede abbia senso, A non può essere vuoto, dal momento che non abbiamo ancora dato significato a un'espressione quale PT(Æ). Quest'insieme può in effetti essere ancora introdotto, ponendosi PT(Æ) = {Æ}, come vedremo nella successiva nota (I.50), con la conseguenza che all'unica funzione esistente in H(Æ,B) si assocerà allora l'unica "partizione" del vuoto, che sarà per convenzione l'insieme vuoto. Inoltre, che la rappresentazione P non è in generale fedele, come si comprende già all'esempio riportato nella Fig. I.1. Infatti, a partire dalla funzione f ivi raffigurata, basta introdurre un'altra funzione f' "permutando" ad arbitrio i tre elementi che costituiscono l'immagine di f, per avere due (e più) diverse funzioni tali che P(f) = P(f') (per costruzione, la partizione indotta in A rimane invece palesemente sempre la stessa).]

Domande-esercizi. Per quali scelte degli insiemi A e B, P può risultare fedele? E quando P non è fedele, come si può concepire a sua volta la partizione associata a P? Come sono fatti i suoi blocchi? Inoltre, P può risultare qualche volta suriettiva? (Si cerchi di dare risposta alle ultime tre domande in un caso particolare che riguardi due insiemi finiti "piccoli" scelti ad arbitrio, e praticando quindi un po' di utile "matematica sperimentale"). Ricordando poi quanto si era detto alla fine della I Parte del presente capitolo, a proposito di partizioni più o meno fini di un'altra, si cerchi di dare senso alle espressioni: in PT(A) esistono una partizione minima (meno fine di qualsiasi altra partizione), che è uguale al singleton {A}, e una partizione massima (più fine di qualsiasi altra partizione), che è uguale all'immagine della rappresentazione rA di cui al punto (I.28).

(I.45) Nota. Si osservi che alle seguenti relazioni, tutte corrette:
A Í A ; A Î P(A) ; {A} Í P(A) ; {A} Î P(P(A)) ;
si possono affiancare adesso le seguenti, tutte ugualmente corrette:
{A} Î PT(A) ; PT(A) Í P(P(A)) ; PT(A) Î P(P(P(A))).

Riprendiamo il discorso, partendo da quella "coincidenza", visibile nell'esempio di cui alla Fig. I.44, per cui gli elementi dell'immagine di f sono esattamente tanti quanti i blocchi della partizione Pf. E' "ovvio" che ad un blocco di Pf può essere associato un unico elemento di B, che risulta anzi un elemento di Im(f), che blocchi distinti corrispondono a elementi distinti di Im(f), e infine che ogni elemento di Im(f) corrisponde inversamente a uno, ed un solo, blocco di Pf. Con la terminologia abbiamo accuratamente costruito, tutte queste circostanze si riassumono dicendo che una funzione f tra due insiemi A e B, comunque vengano assegnati A, B ed f (per il momento A ¹ Æ), induce un isomorfismo tra Pf ed Im(f). Detto tale isomorfismo , è chiaro che, in conformità alle notazioni precedenti, esso può essere formalmente descritto nel seguente modo:

                                                : Pf         ®            Im(f)
[x] Î Pf       ([x]) = f(x) Î Im(f)

(si rammenti che gli elementi di Pf sono blocchi di A, e che ciascuno di essi si può appunto scrivere nella forma [x], per qualche elemento x Î A; naturalmente, tale scrittura non è in generale univoca, nel senso che uno stesso blocco che contenga più di un elemento di A, diciamo x e x', con x ¹ x', si può designare tanto come [x], quanto come [x']).

L'isomorfismo  diventa costituente essenziale di un fondamentale teorema di decomposizione di una funzione, un asserto sostanzialmente semplice, e che possiamo dire di natura meramente logica. Al suo enunciato premettiamo l'ovvia osservazione che, comunque data una partizione P di un insieme non vuoto A, esiste sempre una corrispondenza naturale tra A e P, che chiamiamo proiezione canonica di A su P (perché sarà sempre manifestamente suriettiva, e "assomiglia" quindi al morfismo descritto nella Fig. I.41). Indicata con la lettera p, essa risulta definita dalle seguente regola:

                                               p : A         ®            P
a Î A        p(a) = [a] Î P,

cioè, in parole, p manda un elemento a di A nel corrispondente blocco, elemento di P, ovvero nel blocco di P che contiene a (con la conseguenza che è lecito scrivere: a Î p(a)).

Quanto appena detto poteva anche descriversi introducendo, a fianco del morfismo P, un altro morfismo canonico (a cui non diamo "nome"):
PT(A) ® H(A,P(A)), il quale, ad ogni partizione P del nostro dato insieme A, non associa esattamente la funzione p che abbiamo dianzi definita, che ha codominio "variabile", in quanto va solo da A a P, bensì la sua estensione p' da P a P(A) (si rammenti che infatti P Ì P(A)). Naturalmente, l'immagine di p' è proprio la partizione P di cui trattasi.

Orbene, tutto quanto sopra specificato si può riassumere nella costruzione del seguente diagramma (questa può essere ritenuta una definizione implicita-ostensiva del concetto di diagramma, il quale pure si potrebbe però convenientemente precisare facendo ricorso al linguaggio delle categorie):

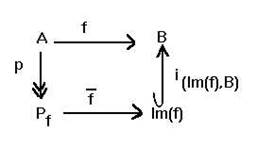
(Fig. I.46)

e nell'osservazione che la funzione f risulta il prodotto delle altre tre funzioni che in esso compaiono, nell'unico ordine possibile, ovvero che:

(I.47) f = i(Im(f),B)oop

(le parentesi sono omesse in virtù della proprietà associativa del prodotto operatorio; in un caso come quello attuale, il diagramma si dice commutativo, la nozione esprimendo la circostanza che tutti i morfismi a priori distinti, ottenuti tramite prodotto operatorio attraverso diversi "cammini" che vanno da un vertice all'altro del diagramma, risultano poi di fatto uguali).

La (I.47) esprime esattamente l'annunciato "teorema di decomposizione", il quale si può enunciare a parole dicendo che ogni funzione si spezza univocamente nel prodotto di tre fattori, che sono (in ordine inverso): (1) una suriezione su un insieme quoziente di A (si ricordi infatti che una partizione si dice anche un "insieme quoziente" di A); (2) un opportuno isomorfismo; (3) un'inclusione (che è una particolare iniezione). Notiamo che il teorema si può precisare asserendo che l'isomorfismo  è univocamente determinato dalle altre "condizioni al contorno", nel senso che nessun altro isomorfismo tra Pf ed Im(f) (e potrebbero essercene numerosi, vedi il prossimo capitolo per il calcolo di Iso(X,Y) in generale, dati cioè due qualsiasi insiemi X e Y) può essere sostituito al posto di  nell'identità (I.47).

Un caso particolare del precedente teorema è quello in cui la funzione f è già un epimorfismo, ovvero B è, come si dice, un'immagine omomorfa di A. Il "diagramma quadrato" della Fig. I.46 si riduce allora a un "triangolo":

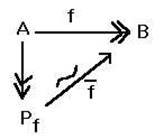
(Fig. I.48)

e il teorema di decomposizione si può enunciare nel seguente modo:

(I.49) I Teorema di omomorfismo. Ogni immagine omomorfa B di un dato insieme A è isomorfa a un insieme quoziente Pf di A, e se è dato esplicitamente un epimorfismo f da A verso B, allora esiste un unico isomorfismo naturale  associato ad f che stabilisce tale relazione tra B e il corrispondente insieme quoziente Pf di A.

(I.50) Nota. Si rifletta sulla circostanza che la condizione restrittiva inizialmente introdotta, cioè che A non sia l'insieme vuoto, non è più necessaria nel caso del teorema di decomposizione, il quale si riduce in questo caso banalmente alla seguente identità:
i(Æ,B) = i(Æ,B)oidÆoidÆ. Infatti, Im(i(Æ,B)) = Æ, e si può introdurre come unico insieme quoziente dell'insieme vuoto (unica sua immagine omomorfa) l'insieme vuoto stesso. Si osservi che chiamare il vuoto un insieme quoziente del vuoto significa dire che si conviene che l'insieme PT(Æ) sia il singleton {Æ}, anziché il vuoto stesso, come dovrebbe in effetti risultare stando strettamente alla definizione scelta per il concetto di partizione (si osservi che, in ogni caso, anche i blocchi dell'unica partizione del vuoto possono dirsi soddisfare alla condizione di non essere vuoti, perché non ce ne sono, ovvero, detta J tale partizione deve considerarsi corretta la seguente implicazione: " B Î J Þ B ¹ Æ!). Però, mentre il vuoto deve allora considerarsi, come sottoinsieme di P(Æ), una partizione del vuoto, ecco che il vuoto come sottoinsieme di un insieme delle parti P(A) non deve considerarsi una partizione di A, se l'insieme A non è vuoto (coerentemente peraltro con il fatto che H(A,Æ) = Æ, se A ¹ Æ). Quella appena proposta è comunque una convenzione utile per dare senso anche a questo solito fastidioso caso limite.

In generale, ogni insieme non vuoto A ammette una "minima" immagine omomorfa, che è un qualsiasi singleton, e una "massima", che è l'insieme A stesso (la minima e la massima sono quindi coincidenti se A è un singleton, e solo in questo caso, se, come è ora supposto, A ¹ Æ), o uno ad esso isomorfo. Corrispondentemente, le rispettive partizioni coincidono con quelle minima e massima di cui si era dianzi parlato.

Accrescono le nostre conoscenze in tema di immagini omomorfe di un dato insieme A due altri significativi enunciati, che si affiancano al I teorema di omomorfismo andando a costituire il II e III teorema di omomorfismo. Essi riguardano sostanzialmente lo studio delle immagini omomorfe C di una data immagine omomorfa B di un dato insieme A; prima, indagando le relazioni che intercorrono tra il "pull-back" da B ad A di un'assegnata partizione P di B, e la partizione Pf indotta da f su A (a norma del teorema (I.49)), e caratterizzando inoltre quelle partizioni di A che si possono ottenere per questa via; poi, illustrando l'ovvia relazione che intercorre tra una di queste partizioni di A (un insieme quoziente appunto di A) e quell'unica partizione P di B da cui essa "proviene" (un insieme quoziente appunto di B).

Premettiamo agli enunciati dei teoremi in parola un lemma, che prende le mosse dalle operazioni di "derivazione" di due nuove funzioni pull-back e push-down a partire da una funzione f (vedi il punto (I.30)). E' chiaro che, derivando ancora dalle f* : P(A) ® P(B) e f* : P(B) ® P(A), si ottengono ben quattro funzioni, ovvero, mantenendo l'ordine di presentazione, (f*)* , (f*)* , (f*)* , (f*)* , il cui dominio e codominio non stiamo qui a precisare, dal momento che una sola di queste ci interessa particolarmente, ovvero (f*)* : P(P(B)) ® P(P(A)), della cui azione sui sottoinsiemi di P(B) non è difficile rendersi conto. Assegnato infatti uno di tali sottoinsiemi Z = {X, Y etc.}, con X, Y Í B, risulta semplicemente ((f*)*)(Z) =  {f*(X), f*(Y) etc.}, e l'insieme ((f*)*)(Z) si dirà ancora il pull-back di Z da B ad A, che denoteremo sinteticamente con pb(Z) (poiché l'intelletto può smarrirsi dietro a tante parentesi, e simboli che si assomigliano, è bene cercare di "visualizzare" la costruzione in parola, e se si vogliono comprendere tutte e quattro le funzioni di cui sopra, sarà bene collocarsi in un caso particolare, per esempio quello illustrato nella figura I.41). Orbene, sussiste il seguente:

(I.51) Lemma. Siano comunque dati due insiemi A e B, un epimorfismo da A verso B, f : A  B, e una partizione P Î PT(B), P Í P(B), P Î P(P(B)). Orbene, il pull-back pb(P) Î P(A) è una partizione di A, meno fine della partizione Pf indotta da f su A, P Ð Pf.

Dim. "Facile", nel senso preciso che essa consegue direttamente dalle definizioni degli enti in gioco, ed è sicuramente più facile "visualizzarla" che non esprimerla attraverso simboli logici. Solo un cenno sulla questione del "meno fine". Se si prende un singolo elemento b Î B in uno dei blocchi C Î P, è chiaro che f*(C) contiene tutti gli elementi a Î A tali che f(a) = b, e quindi che f*(C) contiene quel blocco di Pf che abbiamo chiamato [a], ossia che un singolo blocco f*(C) di pb(P) è costituito esattamente da un'unione di blocchi di Pf. ä

E' facile enunciare adesso il:

(I.52) II Teorema di omomorfismo. Il precedente morfismo
pb : P(P(B)) ® P(P(A)) si restringe, tramite una doppia restrizione di dominio e di codominio, a un morfismo (che chiameremo ancora pull-back, usando sempre lo stesso simbolo pb per designarlo) pb: PT(B) ® PT(A). Tale pb risulta un monomorfismo, la sua immagine è proprio l'insieme di tutte le partizioni di A meno fini di Pf, sicché esse alla resa dei conti costituiscono un insieme isomorfo a PT(B). La corrispondenza inversa tra Im(pb) e PT(B) non è altro che il "push-down", nel senso che, comunque data una partizione Q di A, Q Î Im(pb), vale a dire Q meno fine di Pf, allora pb-1(Q) risulta quella partizione di B che ha come blocchi le immagini dirette f*(C) dei blocchi C di Q.

Dim. L'enunciato piuttosto lungo comporta una serie di affermazioni particolari da dimostrare, ma tutte invero assai semplici. Per esempio, se P e P' sono due diverse partizioni di B, supponiamo quindi che C sia un blocco di P che non è un blocco di P', allora f*(C) è un blocco di pb(P) che non è un blocco di pb(P'). Infatti, se lo fosse, allora f*(f*(C)) = C sarebbe un blocco di P', contro l'ipotesi (abbiamo usato (I.30XIV), tenendo conto che f è supposta suriettiva), etc. etc.. Si noti infine che il simbolo pb-1 ha attualmente senso in relazione all'isomorfismo pb: PT(B) ® Im(pb), ma si introduce così un nuovo abuso di notazione. ä

L'analisi si conclude con il seguente teorema, il quale esprime sostanzialmente la scontata osservazione che un'immagine omomorfa di un'immagine omomorfa di A è un'immagine omomorfa di A (si rammenti (I.26)), e descrive esattamente sia la partizione di A sia l'isomorfismo canonico che rimangono individuati da detta immagine omomorfa:

(I.53) III Teorema di omomorfismo. Ferme restando le notazioni precedenti, esiste un unico isomorfismo F tra P e pb(P), tale che il seguente diagramma risulti commutativo:

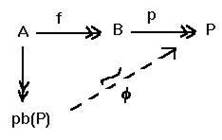
(Fig. I.54)

(dove p è naturalmente la proiezione canonica di B in P, e il morfismo verticale "senza nome" è l'analoga proiezione canonica di A in pb(P); in altre parole, manifestamente, pb(P) risulta la partizione di A associata all'epimorfismo pof. Due parole ancora sulla convenzione di indicare, in siffatti diagrammi, i morfismi che sono noti a priori con frecce "intere", e quelli "da trovare" con frecce "tratteggiate").

Dim. Si tratta di asserto che risulta anch'esso del tutto "ovvio" in virtù delle definizioni: due blocchi distinti di P hanno pull-back distinti in pb(P), ovvero gli elementi di pb(P) sono "tanti quanti" gli elementi di P, etc.. L'isomorfismo F resta naturalmente individuato dalle seguenti identità: F([a]) = (pof)(a) = [f(a)], dove [a] è il blocco di pb(P) che contiene un elemento (arbitrario) a Î A, mentre [f(a)] è il blocco di P che contiene f(a). ä

Approfondimento. Il pull-back dianzi esaminato risolve un problema del tipo illustrato nel seguente diagramma, dove, come abbiamo detto, le frecce "intere" vanno interpretate come i "dati" del problema, e quelle tratteggiate si debbono invece determinare; in questo caso si deve anche determinare l'insieme indicato con il punto interrogativo, con la condizione che sia proprio un insieme quoziente di A:

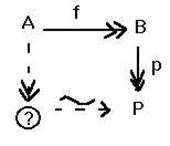
(Fig. I.55)

Un analogo "problema", anziché di pull-back, di push-down, sarebbe quello che si ottiene, dualmente, sostituendo agli epimorfismi dei monomorfismi:

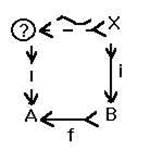
(Fig. I.56)

e la sua "soluzione" appare più o meno immediata (al posto del morfismo p troviamo un morfismo i, da "iniezione"). Relativamente più difficili sono invece i due seguenti problemi, sempre di pull-back e di push-down nell'ordine:

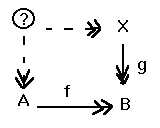
(Fig. I.57)

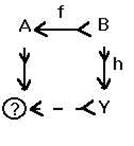
(Fig. I.58)

ai quali dedicheremo qualche attenzione nella già annunciata appendice. Aggiungiamo infine che tutta la precedente analisi potrebbe-dovrebbe essere integrata dal confronto dei due diagrammi che si ottengono dalla Fig. I.46 quando si abbiano due funzioni f . A ® B, e
g: B ® C, con il terzo diagramma che corrisponde alla funzione composta gof : A ® C, ma per il momento soprassediamo.

(I.59) - Può essere istruttivo mettere alla prova le nozioni che precedono nel caso del morfismo immagine, vale a dire nel caso del particolare morfismo
W : H(A,B) ® P(B), che associa ad ogni morfismo f tra A e B, la sua immagine Im(f) come sottoinsieme di B, e quindi come elemento di P(B) (come prima, avremmo dovuto scrivere WH(A,B), oppure W (A,B), ancora un simbolismo troppo "pesante" e non del tutto indispensabile). In quali casi W risulta iniettiva? E cosa si può dire della sua eventuale suriettività, riflettendo sulla circostanza che Im(f) risulta comunque "più piccola" di A? (si ragioni una volta di più nel caso di insiemi A e B finiti). Come è fatto il blocco [f] di un elemento f Î H(A,B) rispetto alla partizione associata a W? Suggerimento: dato un qualsiasi sottoinsieme S Í B, si prenda in considerazione il morfismo naturale iniettivo che abbiamo chiamato ext tra H(A,S) e H(A,B), vale a dire, per una data funzione g Î H(A,S), la funzione i(T,B)og Î H(A,B), e posto T = Im(f), per una data f Î H(A,B), si "guardi" al sottoinsieme Epi(A,T) Í H(A,T)...

(I.60) - Un altro istruttivo esempio potrebbe consistere nello studio dell'insieme delle bipartizioni BPT(A) di un qualsiasi insieme non vuoto A, ovviamente BPT(A) Í PT(A) (quando l'inclusione risulta davvero impropria?). Trascurato il caso banale per cui BPT(A) risulta vuoto (quando A è un singleton; il caso
A = Æ diventa una volta di più un caso "di lana caprina", perché se pur si è convenuto che sia opportuno porre PT(Æ) = {Æ}, e quindi diverso dal vuoto, come si dovrà chiamare quell'unica "partizione" che in PT(Æ) compare? Certamente non una bipartizione, questo caso dovendosi logicamente paragonare a quello di un singleton, sicché sembra lecito affermare che
BPT(Æ) = Æ; ma, ripetiamo, non conviene affaticare la memoria cercando di ricordare siffatte "identità"), e detto P''(A) il sottoinsieme di P(A) costituito da tutti i sottoinsiemi di A diversi dal vuoto e dall'intero A (indicheremo invece con P'(A), quando necessario, il sottoinsieme di P(A) costituito da tutti i sottoinsiemi di A diversi dal vuoto), è chiaro che esiste una funzione naturale
Q : P''(A) ® BPT(A), che associa ad ogni sottoinsieme T Í B la bipartizione {T, CA(T)}. Q è iniettiva? Q è suriettiva? Come è fatta la partizione di P''(A) associata a Q? Data risposta a quest'ultima domanda, si comprenderà subito perché si dice che Q è una corrispondenza di tipo (2,1) tra A e B (mentre una corrispondenza iniettiva sarà detta ovviamente di tipo (1,1), il che, si badi bene, non vuol dire biunivoca)...

etc. etc.

(I.61) Nota. Molto di quanto precede può essere riassunto nell'immagine del "pesciolino d'oro", che il matematico ricerca in insiemi più o meno grandi, costituiti da tanti altri pesciolini tutti uguali, d'argento. Qualche volta di pesciolini d'oro se ne trovano due, sovente allora "collegati", ed è qualche ulteriore convenzione, talora "nascosta", chiamata a scegliere tra essi; un pesciolino d'oro è un elemento di un insieme che spicca sugli altri in modo "universale", senza cioè che siano necessari per identificarlo un particolare intelletto, o speciali condizioni di tempo e di luogo. [In effetti, qualche volta il pesciolino d'oro è così nascosto che per scoprirlo è necessario proprio lo "sguardo di lince" (d'onde il nome dell'Accademia dei Lincei, che ebbe tra i suoi fondatori Galileo) di un "genio".] Così, le più interessanti rappresentazioni, di solito fedeli, sono quelle naturali, o canoniche, dove la congruità dell'attributo che si aggiunge al termine "rappresentazione" è ovviamente decisa ancora una volta dalla <<logica della ragione>> (vedi la nota (I.18)). Tra di esse naturalmente gli isomorfismi naturali, o canonici, i quali allora permettono di considerare due insiemi, pur diversi, come fossero lo "stesso" insieme, o, in altre parole, due diverse rappresentazioni, appunto, del medesimo "concetto". Si tratta nel complesso di una questione che si potrà cominciare a comprendere meglio dopo che si saranno esaminate varie sue concretizzazioni.

Prodotti cartesiani

Occupiamoci adesso di un concetto che è rimasto fin qui latente, e precisamente quello di coppie di elementi di un dato insieme A, ordinate e non ordinate (da qui sarà poi facile il passaggio alle terne, quaterne, etc.). Abbiamo già detto che gli elementi dell'insieme di funzioni H(N,A) si chiamano le successioni di A. Restringiamo adesso il dominio a uno dei segmenti iniziali dell'insieme N, che sono definiti esattamente (in modo ostensivo) come uno dei seguenti sottoinsiemi di N:

(I.62) s1 = {1} Ì s2 = {1, 2} Ì s3 = {1, 2, 3} Ì ... ,

introducendo di conseguenza gli insiemi di funzioni H(s1,A), H(s2,A), etc., che chiameremo rispettivamente A1, A2, etc.. [La notazione esponenziale è giustificata da un teorema che dimostreremo nel prossimo capitolo, e che possiamo subito enunciare asserendo che il numero degli elementi contenuti in un insieme del tipo H(sk,sn) è precisamente nk, la potenza cioè di base n ed esponente k, sicché è frequente pure la notazione generale AB in luogo di H(A,B), per due insiemi qualsiasi, finiti o infiniti. In definitiva, ecco che il simbolo Ak, dato un qualunque numero naturale k, almeno per il momento, va interpretato più esattamente come un'abbreviazione di .]

Ci sembra che quella di "segmento iniziale" sia una denominazione che non è necessario spiegare, così come pure non appare necessario sottolineare la circostanza che, attraverso le funzioni che sono elementi degli insiemi in oggetto, l'ordine naturale di cui sono "portatori" i segmenti sk si "trasferisce" alla "famiglia" di elementi che le funzioni descrivono. Notiamo soltanto che, con i già richiamati simboli dell'Analisi matematica (vedi le "Osservazioni importanti" all'inizio della II parte del presente capitolo), risulta, " k Î N:

sk = [1,k] = {" x Î N ½ 1 £ x £ k},

ma anche (con simbolismo altrettanto usuale):

sk = [1,k+1[ = {" x Î N ½ 1 £ x < k+1},

il che significa che ognuno di questi intervalli chiusi è anche semi-aperto (superiormente), una circostanza che ovviamente non si verifica mai nell'ambito dei numeri reali.

Nella (I.62) è rappresentata una successione di sottoinsiemi finiti di N, la quale risulta monotona crescente, (gli elementi della successione risultano inclusi successivamente l'uno nell'altro), e anzi in senso stretto (le inclusioni di cui trattasi sono tutte proprie). Inoltre, " k Î N, l'insieme sk+1 - sk è un singleton: sk+1 - sk = {k+1}.

L'occasione si presta a una precisazione, in ordine a quell'aggettivo "finito" che abbiamo spesso usato in maniera "intuitiva". Anticipando alcune delle considerazioni che svilupperemo nel prossimo capitolo (ed amplieremo poi nel V), è "chiaro" che l'insieme dei numeri naturali è costruito proprio in maniera tale che quei suoi segmenti iniziali risultino il "prototipo universale" degli insiemi finiti, ovvero, con parole "difficili", che un insieme X è finito ses è la rappresentazione fedele di uno di questi insiemi canonici, ovvero anche che:

(I.63) Un insieme X è finito ses $ k Î N ½ Iso(X,sk) ¹Æ .

L'asserto precedente ammette le seguenti specificazioni:

(I.64) Se un insieme X è finito, allora: $! k Î N ½ Iso(X,sk) ¹ Æ ; vale a dire, chiamato questo numero naturale k la cardinalità, o l'ordine, dell'insieme finito X, in simboli  = k, risulta: " l Î N, l ¹ k Þ Iso(X,sl) = Æ .

(I.65) Se X è un insieme finito, ogni altro insieme Y per cui risulta
Epi(X,Y) ¹ Æ è pure finito, e il suo ordine  risulta non inferiore (maggiore o uguale) a . Sussiste inoltre l'uguaglianza  =  ses Iso(X,Y) ¹ Æ .

(I.66) Se X è un insieme finito, ogni altro insieme Y per cui risulta
Mono(Y,X) ¹ Æ è pure finito, e il suo ordine  risulta non superiore (minore o uguale) a .

(I.67) Corollario. Tutti i sottoinsiemi di un insieme finito sono finiti.

(Ragionando in modo strettamente formale, la peraltro "ovvia" proposizione precedente è "corollario" della (I.66) data l'esistenza, nella condizione Y Í X, dell'inclusione canonica i(Y,X), di cui al punto (I.27)).

Prima di riprendere la trattazione del tema al quale questo paragrafo è dedicato, osserviamo immediatamente che in tutti gli enunciati che precedono c'è per il momento un'eccezione significativa, vale a dire quella costituita dal solito caso limite dell'insieme vuoto. E' chiaro per esempio da (I.67) che il vuoto dovrà considerarsi un insieme finito, in quanto sottoinsieme di ogni altro insieme (finito o infinito; il secondo termine risulta adesso esattamente precisato come sinonimo di non finito, ovvero tale che " k Î N, Iso(X,sk) = Æ, ma anche questa condizione è "equivalente" alla non finitezza solo se consideriamo quello dell'insieme vuoto un caso a parte), e allora è necessario aggregare a N un nuovo simbolo, il famoso zero, il quale rappresenti la cardinalità, o l'ordine, dell'insieme vuoto (e solo di esso!):  = 0.

Corrispondentemente, designeremo con il simbolo N0 l'insieme {0, 1, 2, 3, ...}, che chiameremo, per ragioni ormai evidenti, l'insieme dei numeri cardinali finiti, con la conseguenza che un numero cardinale finito o è lo zero, o è un numero naturale, dove la particella "o" funge al momento da disgiuntiva. Non solo, ma aggregheremo pure alla successione (I.62) un ulteriore "segmento iniziale" di N, che battezzeremo s0 = Æ, con la conseguenza che tutti i segmenti iniziali di N saranno in realtà:

(I.68) s0 = Æ Ì s1 = {1} Ì s2 = {1, 2} Ì s3 = {1, 2, 3} Ì ... ,

e tutti i teoremi precedenti varranno senza eccezioni, comprendendo cioè anche il caso del vuoto, qualora si utilizzino la (I.68) e l'insieme N0.

(I.69) Nota. Si osservi bene che possiamo interpretare tanto la (1.62), quanto la (I.68), quali successioni di elementi di P(N), nel primo caso attraverso la funzione 1  s1 , 2  s2 , etc., nel secondo attraverso la funzione 1  s0 , 2  s1 , etc. (in effetti, s0 risulta il primo elemento della successione (I.68) etc.); come dire, che non bisogna pensare che i segmenti presenti nella (I.68) possano essere introdotti soltanto come segmenti di N0, anziché di N! In verità, essi sono anche segmenti iniziali di N0, ma la successione di tutti i segmenti iniziali di N0 è la seguente: Æ Ì {0} Ì {0, 1} Ì {0, 1, 2} Ì ... , ed è una successione nel senso che:
1  Æ, 2  {0}, non cambiamo certo la convenzione che il dominio di una successione debba essere N, sostituendogli N0! Ai segmenti di N0 non abbiamo dato per il momento "nome" per evitare equivoci, e del resto quella che stiamo presentemente descrivendo è una costruzione che si adatta a tutti gli insiemi bene ordinati, un concetto che avremo modo di introdurre e commentare adeguatamente in seguito. Per il momento basterà dire che, dato un insieme bene ordinato A, si abbiano in mente come esempi N o N0, il cui primo elemento sia un certo a Î A, per ogni elemento x Î A si può introdurre il segmento iniziale Sx(A), di "estremo" x, definito come l'intervallo [a,x[ (si noti che si sta descrivendo una rappresentazione canonica, e fedele, A ® P(A)), sicché: (1) risulta Sa(A) = Æ, Sa+1(A) = {a}, etc. ("a+1" è una notazione evocativa che si può introdurre anche "in astratto" per definire l'elemento "successivo" di a); (2) S1(N) = Æ, S2(N) = {1}, etc. (questi sono proprio gli insiemi che abbiamo chiamato sk, a partire dall'indice k = 0, nell'ordine: S1(N) = s0, S2(N) = s1, etc.); (3) risulta analogamente: S0(N0) = Æ, S1(N0) = {0}, etc., tutta la situazione dovrebbe riuscire adesso abbastanza chiara.

Torniamo allo studio degli insiemi di funzioni H(sk,A), estendendo per l'esponente k la condizione k Î N alla condizione k Î N0, e considerando quindi, oltre agli insiemi A1, A2, ... un ulteriore insieme A0 = H(s0,A) = H(Æ,A), il quale risulta banalmente, in virtù delle convenzioni che abbiamo accuratamente illustrato, un singleton: A0 = {i(Æ,A)}, con la conseguenza particolare che, per ogni insieme A:

(I.70)  = 1

(la (I.70) vale ovviamente anche nel caso A = Æ; abbiamo già detto che esamineremo soltanto nel prossimo capitolo la cardinalità degli insiemi Ak, ma dato sin da ora che  = k, per ogni cardinale finito k, e per ogni insieme finito A - all'estensione al caso infinito si accennerà nel capitolo V - ecco che l'identità precedente porge n0 = 1 per ogni cardinale finito n, in questo caso n rappresentando l'ordine di A; in particolare, le convenzioni sono poste in maniera tale che risulti valida l'identità: 00 =1).

Esaminato così a fondo il primo termine della successione A0, A1, A2, ... (si noti che si tratta ancora di una successione: 1  A0, 2  A1, etc.), anche il secondo termine risulta alquanto banale, dal momento che, in generale:

(I.71) Se X è un qualsiasi singleton, e A un qualsiasi insieme, H(X,A) risulta naturalmente isomorfo ad A.

Dim. Come dire che l'insieme Iso(A,H(X,A)) è attualmente non vuoto, e che in esso (studieremo pure la "consistenza", o cardinalità, di un insieme del tipo Iso(A,B) soltanto nel prossimo capitolo) esiste anzi un "pesciolino d'oro", un isomorfismo canonico. Si tratta ovviamente (sempre con parole "difficili") della rappresentazione fedele di A che abbiamo già incontrato (punto (I.29)) sotto il nome di cX. In effetti, si comprende subito che tutte le funzioni da X ad A risultano attualmente delle "costanti" (X è un singleton!), e che una di tali funzioni corrisponde a uno ed un solo elemento di A, e viceversa. ä

(Si noti che l'enunciato precedente vale anche nel caso A = Æ, poiché
H(X,Æ) = Æ, e Iso(Æ,Æ) = {idÆ}).

Passiamo adesso al caso successivo, e cioè a quello dell'insieme A2, incontrando così il primo oggetto davvero significativo nella successione oggetto della nostra attenzione. Gli elementi dell'insieme A2, che si indica anche con il simbolo A´A, e si dice il prodotto cartesiano di A per A, precisano esattamente il concetto intuitivo di coppia ordinata di elementi di A, in quanto una funzione da s2 ad A è data proprio specificando un ouput in A corrispondente all'input 1, che sarà quindi il primo elemento della coppia ordinata, e un output in A corrispondente all'input 2, che sarà quindi il secondo elemento della coppia ordinata.

(I.72) Nota. Qualche parola sul perché di quell'aggettivo "cartesiano". L'origine del termine è manifesta, in quanto si dicono appunto cartesiane le coordinate introdotte nel piano ordinario attraverso uno dei noti "sistemi di riferimento" detti anch'essi cartesiani. Attraverso tali coordinate, ogni punto del piano viene ad essere biunivocamente rappresentato con una coppia ordinata di numeri reali.

Saranno allora chiari anche simboli quali A´A´A, etc., e l'introduzione di termini quali terne ordinate, quaterne ordinate, etc., di elementi di A, le quali si chiamano anche le disposizioni ordinate con ripetizioni (sottinteso "eventuali" ripetizioni, specificazione che talvolta viene omessa quando il contesto di riferimento sia "chiaro"; anche ordinate può essere omesso, essendo implicitamente contenuto nel termine "disposizione") di elementi di A, di specie 3, 4 etc.. E' evidente che le disposizioni ordinate con ripetizioni di specie 2 coincidono proprio con le coppie ordinate di elementi di A, mentre le disposizioni di specie 1 si possono identificare, a norma di (I.71), con gli stessi elementi di A, mentre esiste un'unica disposizione di specie 0, sulla cui "natura" non torniamo. Come abbiamo già anticipato, il calcolo del numero di queste disposizioni nel caso di un insieme A finito sarà oggetto di studio del prossimo capitolo, e costituisce il primo argomento della cosiddetta Analisi combinatoria.

Tornando al caso paradigmatico dell'esponente (o specie) uguale a 2, osserviamo che una coppia ordinata di elementi di A (supponiamo adesso A non vuoto!; del resto se A = Æ tutti gli elementi della successione in parola sono vuoti, a eccezione del primo, che è sempre un singleton) si può scrivere in tanti modi, per esempio nella classica forma compatta funzionale f : s2 ® A, oppure in una forma "ostensiva": 1  f(1) = a, 2  f(2) = b, oppure sotto una forma matriciale 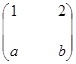, ma più semplice di queste è naturalmente la forma (a,b), dove l'importante è capire però che quel simbolo di parentesi rotonde designa una funzione, che deve avere quindi esattamente determinati dominio e codominio.

Si noti bene la differenza tra un simbolo del tipo {a, b}, e (a,b). Il primo rappresenta un insieme, diciamo un sottoinsieme di A, con due elementi, e quindi la scrittura del simbolo sottintende pure a ¹ b. Il secondo rappresenta una funzione, e quindi non solo può essere a = b, ma bisogna anche intendere
(a,b) ¹ (b,a), naturalmente se a ¹ b, mentre invece il simbolo {a, b} rappresenta lo stesso insieme che il simbolo {b, a}. Naturalmente, anche il simbolo funzionale 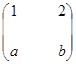 deve essere concepito in maniera tale che esso designi la stessa funzione del simbolo 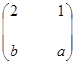, ma è chiaro che la prima è una scrittura che potremmo dire "canonica" della funzione, mentre la seconda, per quanto del tutto lecita (vale a dire "non ambigua") non lo è.

(I.73) Nota. Costituisce da sempre un problema didattico particolarmente delicato quello di far comprendere al principiante la differenza tra il concetto di insieme e il concetto che più tardi preciseremo di insieme ordinato (e vedremo anzi vari "tipi" di ordine, per esempio il "buon ordinamento" di cui alla nota (I.69)). In effetti la differenza non si riesce ad apprezzare soprattutto nel caso di insiemi finiti, o di insiemi per i quali venga data un definizione ostensiva, la quale svolgendosi nel tempo, attribuisce agli elementi dell'insieme un ordine di presentazione che è spesso puramente accessorio e non sostanziale (il tempo, una forma che deve ritenersi unidimensionale, va considerato come l'ordinatore principe, base stessa del "principio di causalità", ovvero della successione causa-effetto; non vogliamo tralasciare l'occasione di sottolineare come l'unidimensionalità del tempo dimostri inequivocabilmente la differenza che deve concepirsi tra pensato - per esperienza soggettiva multidimensionale - e parlato). Si pensi per esempio all'insieme T = {À, a}, costituito dalle due prime lettere degli alfabeti ebraico e greco. Si tratta di un insieme che avremmo potuto introdurre altrettanto bene con la scrittura T = {a, À}, ed è ovvio che ciascuna di queste scritture introduce inevitabilmente un "ordine" che a volte non è forse voluto, o meglio, se voluto deve essere meglio precisato, ricorrendo appunto al concetto di insieme ordinato e non a quello di insieme "semplice". In effetti, T e s2 sono isomorfi, e una data scrittura privilegia uno degli isomorfismi dell'insieme Iso(T,s2), ma trattandosi di insiemi che non sono isomorfi in modo naturale, ecco che non esiste un isomorfismo (nel caso presente ce ne sono soltanto due) che possa ritenersi privilegiato rispetto a un altro. Come dire pure: (1) che T è indecomponibile (ad eccezione che per un ebreo, o per un greco, i quali dovrebbero comunque tenere conto di questa circostanza puramente contingente, e non "universale"), mentre s2 non lo è (anzi, s2 è decomponibile in senso stretto); (2) che T non può essere convenientemente usato per ordinare gli elementi di un insieme. Cioè, H(T,A) è un insieme perfettamente ammissibile, ma non può essere considerato l'insieme delle coppie ordinate di elementi di A: data la funzione
a  f(1) = a, À  b, chi sarebbe il primo elemento della coppia ordinata, e chi il secondo? Vale ancora a dire, nella scrittura A2 è il numero 2 come "ordinale" quello che compare ad esponente, e non il numero 2 come "cardinale", ma si tratta di tutte questioni che potranno comprendersi appieno solo in seguito. Si può notare per finire che risulta invero anche s2 = {1, 2} = {2, 1} (l'unica condizione posta per una presentazione ostensiva di un insieme è che, ripetiamo, i suoi elementi non si ripetano), ma data la natura assai speciale dell'insieme s2 ecco che tra le due scritture è finalmente possibile individuarne una canonica (universale) rispetto all'altra (e volendo bisognerebbe anche distinguere tra esposizioni verbali, che si svolgono sicuramente nel tempo, ed esposizioni scritte, per risalire da una delle quali all'ordine temporale della sua genesi c'è la necessità di conoscere le ulteriori convenzioni grafiche adottate, tipo scrittura da sinistra a destra, o viceversa, o addirittura altri tipi di scrittura)...

La (a,b) non è il modo più semplice possibile per esprimere una coppia ordinata di elementi di A, perché più semplice ancora è ovviamente scrivere: "ab", una banale sequenza di due elementi di A, che si può convenientemente usare quando non ci sia luogo per equivoci (per esempio, 52 potrebbe designare invece tanto il numero cinquantadue, quanto la coppia ordinata (5,2)). ab si dice anche una stringa di A avente lunghezza uguale a 2, e tutte le parole che compaiono in queste dispense non sono invero altro che stringhe, di varia lunghezza, costituite con elementi di un ben determinato alfabeto (comprendente anche particolari segni grafici quali spazi, segni di interpunzione, simboli speciali, etc.). Ecco perché per la teoria di cui ci stiamo occupando si utilizza a volte il suggestivo linguaggio delle stringhe, e l'insieme A di sostegno si denomina un "alfabeto", sicché si capisce cosa sia l'insieme di tutte le possibili stringhe di un insieme A (ripetiamo le stringhe di lunghezza 1 sono identificate con gli elementi di A, mentre esiste anche una stringa vuota, l'unico elemento di A0), che si designa con il simbolo W(A) (la "W" sta per l'iniziale di word):

(I.74) W(A) = A0ÈA1ÈA2ÈA3È... .

Notiamo che, se A è non vuoto, quella che appare nel RHS di (I.74) è una partizione di W(A), e che W(A) è un insieme certamente infinito (W(Æ) è invece un singleton, contente unicamente la stringa vuota sull'insieme vuoto!).

Prima di abbandonare questo argomento, è forse opportuno far notare che W(A) è supporto di una struttura algebrica alquanto interessante, in quanto date due qualsiasi stringhe (precisamente, una coppia ordinata di stringhe, ovvero un elemento dell'insieme W(A)2, la costruzione si può iterare all'infinito!), diciamo "xty", e "gdkp", è possibile effettuare una loro composizione, o prodotto, o perfino "somma" (una somma però non commutativa), semplicemente scrivendo la stringa "xtygdkp" (che ha lunghezza uguale alla somma delle lunghezze delle stringhe fattori), una sorta di giustapposizione che è una delle operazioni chiave che l'intelletto ripropone in tanti diversi contesti (in aritmetica, in geometria e qui). Si tratta, come si comprende subito, di un'operazione eminentemente non commutativa ("gdkpxty" è una stringa diversa da "xtygdkp", così come "roma" è diversa da "amor", o da "maro"), allo stesso modo peraltro del prodotto operatorio tra funzioni, un'operazione che dà luogo a un notevole ulteriore esempio di semigruppo unitario (la stringa vuota funge manifestamente da "unità" del semigruppo), che si affianca ai già noti H(A), per ogni insieme A, e ad altri con cui lo "studente" ha pure estrema familiarità, di cui però diremo qualcosa soltanto nell'annunciata appendice al presente capitolo.

(I.75) Nota. W(A) si dice anche il semigruppo libero generato dall'insieme A, per ragioni di cui difficilmente riusciremo a occuparci in un mini-corso, o corsino, quale quello di Algebra 1. Basterà adesso unicamente accennare al fatto che, in qualche senso, esso è una sorta di semigruppo unitario universale, di cui ogni altro semigruppo unitario è "rappresentazione", va da sé non necessariamente fedele, per qualche scelta dell'insieme A.

(I.76) Un'importante rappresentazione fedele di un insieme A. Per ogni insieme A, si può introdurre il morfismo diagonale dA : A ® A´A, così definito:
dA(a) = (a,a). E' chiaro che si tratta di un isomorfismo di A sulla diagonale
DA = Im(dA) Í A´A (l'inclusione deve essere espressa in senso lato per la presenza dei casi A uguale al vuoto, oppure A singleton, ma è chiaro che in generale si tratta di un'inclusione stretta).

(I.77) Il concetto di prodotto cartesiano ci permette di introdurre in un modo preciso la nozione di operazione. Si cominci con l'osservare che l'ordinaria operazione di somma tra due elementi di N (o se si preferisce di N0) può appunto essere concepita come una particolare funzione + : N´N ® N, allo stesso modo che il prodotto * : N´N ® N, e che in modo analogo si possono descrivere pure tutte le operazioni di unione e di intersezione tra sottoinsiemi di un assegnato insieme A, ovvero: (1) È : P(A)´ P(A) ® P(A) ; (2) Ç : P(A)´ P(A) ® P(A).
Corrispondentemente, si chiama in generale operazione (binaria e interna) su un dato insieme A una qualsiasi funzione A´A ® A, e data comunque una tale operazione w Î H(A´A,A), si dice che la coppia ordinata (A,w) è una struttura algebrica (semplice) di supporto A e di operazione w (che può chiamarsi come si vuole, prodotto, somma, etc., spesso decidono tradizione e contesto, ma si noti che è usuale utilizzare la terminologia e il simbolismo relativi alle somme - notazione additiva - solo in ambito commutativo, mentre in un ambito generale, eventualmente non commutativo, si preferisce usare di solito la notazione moltiplicativa). In luogo del correttissimo e chiarissimo w(a,b), si può usare anche awb, oppure soltanto ab, quando il riferimento ad w sia sottinteso. Tutti gli esempi che precedono (ai quali ci si può riferire, con simbolismo ormai ovvio, come a (N,+), (N,*), (P(A),È), (P(A),Ç), è sempre meglio specificare l'operazione, qualora la semplice indicazione del supporto della struttura non la individui in qualche modo "univocamente") sono relativi a operazioni commutative, ma, per un insieme A generale (vedi quanto se ne dirà precisamente nel prossimo capitolo), il semigruppo unitario (H(A),o), dove o rappresenta il prodotto di composizione tra endomorfismi di A, sarà una struttura algebrica non commutativa. Tutte le strutture algebriche semplici che abbiamo presentato come "esempi" significativi, sono comunque associative, e tali strutture algebriche semplici sono esattamente quelle che diremo in generale un semigruppo (per (P(A),È) e (P(A),Ç) si rammentino le (I.11); l'osservazione che le seguiva mostra invece che, in generale, (P(A),-) è sì una struttura algebrica semplice, ma non un semigruppo). Ripetendo in modo più esplicito e definitivo, un semigruppo, avente come supporto un dato insieme A, e con riferimento a una data operazione w binaria interna su A, è una struttura algebrica semplice (A,w), tale che l'operazione w sia associativa, ovvero, sia tale che: " a, b, c Î A Þ w(w(a,b),c) = w(a,w(b,c)) (e si potrebbe adesso scrivere
" (a,b,c) Î A3), o anche, con altre convenzioni grafiche più "comprensibili": (awb)wc = aw(bwc).

(I.77) Le operazioni di cui sopra sono state dette interne, perché coinvolgono un unico insieme A. Esterna sarebbe invece un'operazione A´A ® B, o anche in generale A´B ® C, introducendo un nuovo simbolo (di prodotto cartesiano tra insiemi distinti!) che presto spiegheremo, ma si noti che in questo caso, in mancanza di ulteriori chiarimenti, non si capisce più quale debba essere considerato l'insieme supporto della struttura. Per tale ragione preferiamo chiamare un'applicazione A´B ® C un'azione, sinistra, di A su B a valori in C (una nomenclatura che si fa sempre più ricca, nella misura in cui si fa sempre più ricca la fenomenologia che cade sotto la nostra attenzione). Binarie, ovviamente, perché coinvolgono coppie ordinate di elementi di A. Vedremo in seguito come si possa rinunciare, quando è il caso, a tali specificazioni restrittive (per esempio in geometria è usuale avere a che fare anche con operazioni esterne, quali il prodotto scalare tra due vettori, che dà come risultato un numero reale), la più semplice "liberazione" dalle quali è di considerare operazioni (sempre interne) ternarie, quaternarie, etc., come funzioni A´A´A ® A, A´A´A´A ® A, etc., che rappresentano però casi piuttosto rari (nella geometria dello spazio ordinario si incontra il cosiddetto prodotto misto tra vettori, come un'operazione ternaria comunque esterna, il cui risultato è un numero reale). Più interessanti di queste, e più "comuni", ci sembrano in effetti le operazioni unarie, interne o esterne, le prime corrispondendo evidentemente agli endomorfismi A ® A, le seconde a funzioni qualsiasi A ® B. Un esempio notevole di operazione unaria interna è dato dalla complementazione nell'insieme P(A), ma tale è anche il passaggio all'opposto, quando si ragioni di numeri reali con segno, o all'inverso, quando si tratti di numeri reali diversi da zero; mentre un'operazione unaria esterna è per esempio quella che costruisce il modulo di un vettore a partire da un vettore, in uno spazio ambiente in cui sia stata fissata una unità di misura. Ma non è il caso di tacere delle pur interessanti operazioni zerarie: dovendosi una di queste (interna) riguardare, in virtù delle convenzioni terminologiche fissate, come una funzione A0 ® A, ecco che il dominio dell'operazione zeraria è in ogni caso un singleton, e che, se A non è vuoto, l'operazione stessa deve essere interpretata come la scelta di un particolare elemento di A. Corrispondentemente, l'esistenza di un eventuale elemento neutro in una struttura algebrica semplice (A,w) può descriversi attraverso l'esistenza di una particolare ulteriore operazione zeraria da affiancare alla w (il vuoto può considerarsi come supporto di un'unica struttura algebrica semplice che deve ritenersi un semigruppo, (Æ, Æ´Æ ® Æ), che non è però un semigruppo unitario perchè non c'è nessuna operazione zeraria definibile sul vuoto, in quanto H(Æ0,Æ) = Æ, dal momento che Æ0 è un singleton e non è il vuoto; il paradosso qui è che il vuoto può ritenersi per esempio supporto di operazioni binarie interne, ma non zerarie interne).

(I.78) Un esempio notevole di operazioni unarie esterne è quello che riguarda la "formalizzazione" del concetto di somma o intersezione di una totalità qualsiasi di insiemi (si veda la "puntualizzazione" che segue l'introduzione del concetto di partizione), specifichiamo però: sottoinsiemi di un fissato insieme A. Dato un qualsiasi sottoinsieme X Í P(A), si può definire l'unione o l'intersezione degli elementi di X come un sottoinsieme di A, che si può indicare rispettivamente con È(X) o Ç(X), ed ecco che abbiamo definito due operazioni importanti (si noti come si tratti sempre delle "stesse cose", nel presente caso di semplici funzioni, ma la terminologia è diversa a seconda del contesto semantico in cui esse si presentano!):

P(P(A)) ® P(A), X  È(X),
P(P(A)) ® P(A), X  Ç(X).

Tali operazioni si possono evidentemente "estendere" al caso di famiglie qualsiasi di sottoinsiemi di A, attraverso le seguenti ovvie posizioni:

H(I,P(A)) ® P(A), F  È(Im(F)),
H(I,P(A)) ® P(A), F  Ç(Im(F))

[Si rammenti che una famiglia di sottoinsiemi di A di indici I è semplicemente una funzione F da I a P(A) - usiamo adesso un carattere maiuscolo per evidenti motivi - e che quindi Im(F) è un sottoinsieme di P(A), ovvero un elemento di P(P(A))].

[Se si prende una qualsiasi funzione f: A ® B, e si interpreta per " X Í B la funzione pull-back f°X : X ® P(A) come una "famiglia" di sottoinsiemi di A, è chiaro che il morfismo pull-back f* : P(B) ® P(A) rimane collegato ad f° mediante la seguente costruzione: f*(X) = È(Im(f°X) - si rammentino le (I.24) e (I.30). Con il simbolo f°X abbiamo ovviamente indicato la restrizione della funzione f° : B ® P(A) al sottoinsieme X di B.]

(I.79) Il caso delle coppie non ordinate, o in generale dei prodotti simmetrici A[k] come insiemi quoziente degli insiemi Ak. Si potrebbe pensare che una coppia non ordinata di elementi di A sia la stessa cosa che un sottoinsieme di A con due elementi, [Designeremo l'insieme di tali sottoinsiemi con il simbolo auto-esplicativo P2(A); in generale, per ogni insieme A, e per ogni numero cardinale finito k,
Pk(A) Í P(A) sarà quel sottoinsieme dell'insieme delle parti di A costituito da tutti quei sottoinsiemi di A che hanno precisamente k elementi, sicché in particolare P0(A) = {Æ}, e Pk(A) = Æ se A è un insieme finito e k è maggiore dell'ordine n di A; ancora, in questo caso, Pn(A) = {A}, mentre, sia se A è non vuoto sia se A è vuoto, risulta P1(A) = Im(rA), vedi punto (I.28).] ma se uno di questi sottoinsiemi "individua" certamente una coppia non ordinata di elementi di A, ecco che non è opportuno "identificare" una tale coppia con uno di essi, perché in tale modo non si otterrebbero tutte le coppie desiderate, dovendosi comprendere nel concetto anche il caso che la coppia non ordinata abbia ripetizioni, ossia che si tratti della coppia non ordinata [a,a] (usiamo questo simbolo usuale, che fa ricorso alle parentesi quadrate, già usate per denotare i blocchi di una partizione, anche se attualmente rischia di confondersi con gli intervalli chiusi e limitati dell'Analisi). Il modo migliore di definire quello che diremo il prodotto simmetrico A[2] dell'insieme A relativo all'esponente 2, con manifesto riferimento al prodotto cartesiano A2, è di introdurre un'opportuna partizione nell'insieme A2, e chiamare A[2] proprio codesta partizione, con l'effetto che il prodotto in parola riuscirà un insieme quoziente del prodotto cartesiano. Facile è comprendere come si debba procedere, in quanto se a ¹ b bisognerà costruire un blocco comprendente entrambe le coppie ordinate (a,b) e (b,a), mentre se a = b il blocco corrispondente alla coppia (a,a) conterrà un unico elemento, appunto la coppia in oggetto. Per riassumere, il simbolo [a,b], quando a ¹ b, designerà esattamente l'insieme {(a,b), (b,a)}, mentre la coppia non ordinata [a,a] sarà il singleton {(a,a)}, e non l'insieme {a}. Notiamo ancora che la proiezione canonica
p : A2  A[2] induce ovviamente (per banale restrizione di dominio) una corrispondenza (2,1) (vedi punto (I.60)) di A2-DA (vedi punto (I.76)) su
A[2]-p(DA), e che quest'ultimo insieme è manifestamente isomorfo, e in modo naturale, a P2(A), d'onde quella possibile "identificazione", ma appunto solo "parziale", con cui avevamo iniziato la presente argomentazione.
Si comprenderà certo adesso come si possano estendere le precedenti considerazioni al caso di un esponente k qualsiasi, comprendente i casi limite banali k = 0 e k = 1, fino a parlare dei prodotti simmetrici generali A[k] come insiemi quoziente dei prodotti cartesiani generali Ak, collegati a questi da una proiezione canonica p : Ak  A[k] che è meno semplice però visualizzare bene come nel caso k = 2, perché adesso saranno molte di più le k-ple non ordinate con eventuali ripetizioni, e bisogna concepire per esempio ben distinta la terna [a,a,b] = {(a,a,b), (a,b,a), (b,a,a)} dalla terna [a,b,b] = {(a,b,b), (b,a,b), (b,b,a)}. In parole difficili, e per esempio, una terna (a,b,c) Î A3 deve costituire blocco unico con tutte le altre analoghe terne che si ottengono da quella "permutandone" ad arbitrio gli elementi, e si vede facilmente che sono 6 nel caso in cui gli elementi a, b c, siano a due a due distinti tra loro, 3 nel caso in cui due soltanto degli elementi a, b, c vengano a coincidere, 1 infine nel caso
a = b = c. Di siffatti calcoli, e del calcolo generale della cardinalità di un prodotto simmetrico A[k] quando la base A sia finita, ci occuperemo sempre nel prossimo capitolo, a proposito di Analisi combinatoria. Per il momento avvertiamo soltanto che chiameremo gli elementi di A[k], oltre a k-ple non ordinate di elementi di A, anche combinazioni con (eventuali) ripetizioni di elementi di A presi a k a k, o di specie k (e valgono le considerazioni già fatte per il termine "disposizioni": combinazioni contiene già in sé implicitamente il riferimento all'assenza di un ordinamento).

(I.80) Definizione del prodotto cartesiano A´B tra due insiemi qualsiasi A e B, dati nell'ordine, ovvero, una coppia ordinata di insiemi (A,B). E' facile generalizzare la precedente "operazione" di prodotto cartesiano dal caso A´A, due "fattori" uguali, al caso di due fattori qualsiasi. Si tratta prima di tutto di considerare l'insieme unione AÈB, poi l'insieme
H(s2,AÈB) = (AÈB)´(AÈB) = (AÈB)2, e infine di prendere in quest'ultimo tutte le funzioni f tali che f(1) Î A, f(2) Î B. Ovvero, coppie ordinate del tipo (a,b), dove il primo elemento a sia in A, e il secondo b in B (non ci si confonda con il caso di prima, in cui b era semplicemente un simbolo per indicare un secondo elemento sempre in A!).
E' chiaro che un prodotto cartesiano A´B è il dominio di due funzioni naturali,
che si dicono le proiezioni canoniche del prodotto sui rispettivi fattori:
prA : A´B ® A, prA((a,b)) = a ; prB : A´B ® B, prB((a,b)) = b,
le quali sono manifestamente suriettive se i due fattori A e B sono entrambi non vuoti (quando per esempio A = Æ, B ¹ Æ, risulta invece A´B = Æ, e mentre la prima proiezione risulta suriettiva, la seconda, che coincide con il morfismo inclusione del vuoto in B, non lo è!), e si indicano anche con i simboli più semplici pr1 e pr2, o p1 e p2 (si noti del resto che le proiezioni in parola sono due, distinte, e che la notazione prA, prB, risulta quindi ambigua nel caso A = B). Tali proiezioni, assieme ai loro pull-back (vedi (I.24)), (prA)° e (prB)°, permettono di visualizzare un prodotto cartesiano, come un insieme doppiamente fibrato, rispettivamente su A e su B (vedi anche la Fig. I.41, e la successiva introduzione del termine fibra di una "proiezione"; in generale di una qualsiasi suriezione, ma volendo si può anche parlare di "fibre vuote"):

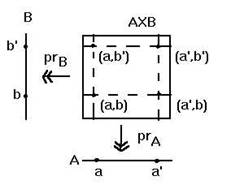
(Fig. I.81)
(Un'immagine "mentale" del prodotto cartesiano tra due insiemi A e B,
rappresentati come due segmenti, rispettivamente orizzontale
e verticale; le fibre su A sono segmenti verticali di A´B,
quelle su B sono segmenti orizzontali)

[Forse sarebbe stato più opportuno enfatizzare la "differenza" tra A e B disegnando uno dei due segmenti più corto dell'altro, ovvero, rappresentando un rettangolo in luogo di un quadrato; ma tant'è, il disegno ormai è fatto, e sarà la fantasia dello studente a "modificarlo" come meglio ritenga conveniente.]

Ripetiamo che, se A e B non sono vuoti, si tratta di due partizioni notevoli dell'insieme prodotto cartesiano, che risultano isomorfe in modo naturale ai due fattori del prodotto!

Ci farà comodo nel seguito aver enunciato subito una "proprietà universale" del prodotto cartesiano, che lo caratterizza a meno di isomorfismi.

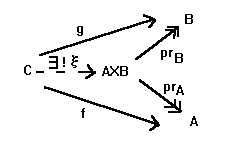
(Fig. I.82)
(La proprietà universale del prodotto cartesiano)

Ritorniamo al fatto che A´B è un insieme dotato di due proiezioni canoniche,
prA : A´B ® A, prB : A´B ® B, e meditiamo sulla circostanza che, se C è un qualsiasi altro insieme, e se f Î H(C,A), g Î H(C,B) sono due qualsiasi funzioni di dominio C e di codominio così specificato, è possibile allora costruire un'unica funzione, che nella precedente figura è indicata con il simbolo x come una "incognita" (vedi appendice per ulteriori considerazioni su equazioni che possiamo dire "funzionali"), ma che a "conti fatti" potremmo indicare con il simbolo f´g, di dominio sempre C, ma di codominio A´B, tale che risulti:
f = (prA)ox , g = (prB)ox
(ovvero, i due "triangoli" da cui è formato il precedente diagramma sono "commutativi").
E' chiaro che la coppia di equazioni indicata ha un'unica soluzione, e precisamente: " c Î C , x(c) = (f(c),g(c)) Î A´B
(la funzione x(c) dianzi definita soddisfa manifestamente alle due condizioni enunciate; viceversa, se x(c) = (ac,bc) è una qualsiasi altra funzione che le soddisfa, con simbolismo che si spera ovvio, deve risultare:
f(c) = ((prA)ox)(c) = prA(x(c)) = prA(ac,bc) = ac,
g(c) = ((prB)ox)(c) = prB(x(c)) = prA(ac,bc) = bc,
e quindi proprio x(c) = (f(c),g(c)), come affermato),
che abbiamo proposto di chiamare, per evidenti motivi, f´g, anche se si tratta di un "abuso di notazione" (se non di concetto). Infatti, data la situazione generale:
j : X ® Y , c : Z ® T , ecco che risulta naturale porre
j´c : X´Z ® Y´T , (j´c)(x,z) = (j(x),c(z)) (con simbolismo autoevidente),
sicché la precedente f´g non è questa f´g : C´C ® A´B, bensì la restrizione di tale ultima funzione alla diagonale DC, composta poi con l'isomorfismo canonico tra C e appunto DC, una situazione più difficile a illustrare che a "capire":
C  DC  C´C ® A´B .
Quello che conta è che il prodotto cartesiano A´B abbia una tale proprietà, e che essa lo caratterizza, a meno di isomorfismi, nel senso che: se Z è un altro qualsiasi insieme, dotato di due "proiezioni canoniche" p1 e p2 su A e B rispettivamente, tali che il "complesso" dei dati goda della stessa proprietà universale del prodotto cartesiano, allora esiste un solo isomorfismo tra Z ed A´B che si "comporti bene", renda cioè "tutti i possibili" diagrammi commutativi. Basta ragionare sul fatto che, in virtù delle considerazioni precedenti, esiste certamente un unico morfismo a da Z ad A´B che soddisfa le due equazioni p1 = (prA)oa, p2 = (prB)oa, ma inversamente, per ipotesi, ne deve esistere anche un altro, diciamolo b, da A´B a Z, tale che risultino soddisfatti le equazioni: prA = (p1)ob, prB = (p2)ob, e prestando un po' di attenzione si capisce come aob non possa che essere l'identità di A´B, allo stesso modo che boa non può che essere l'identità di Z. [Si noti che la proprietà universale del prodotto cartesiano ha l'ovvia conseguenza che nessun endomorfismo di A´B, eccettuata l'identità idA´B, può soddisfare le due equazioni: prA = (prA)ox, prB = (prB)ox ; infatti la citata identità le soddisfa, e sappiamo che la soluzione non può che essere unica! Aggiungiamo che, quando si "lavora" in siffatti contesti si dice che si sta facendo operazione di diagram chasing, un'attività che eserciteremo frequentemente nell'appendice.]

(I.83) Un divertissement. Comunque presi due insiemi A e B non vuoti, il prodotto cartesiano dianzi definito risulta di fatto tale che le due proiezioni prA e prB sono suriettive. Ma noi potremmo pensare di introdurre un prodotto cartesiano Z di A per B definendolo per il tramite della detta proprietà universale, vale a dire di introdurre il "complesso" formato dall'insieme Z, di natura non meglio specificata, e da due morfismi p1 : Z ® A, p2 : Z ® B, di cui si sa solo a priori che essi soddisfano alla condizioni sopra illustrate (se A è per esempio uguale al vuoto, allora si sa subito che Z è di necessità pure vuoto, altrimenti non esisterebbe p1). Come si fa a dimostrare direttamente che p1 e p2 sono allora necessariamente suriettive (ricordando che A e B sono supposti entrambi diversi dal vuoto), senza passare attraverso il nominato isomorfismo "diagrammatico" del complesso (Z,p1,p2) con il complesso (A´B,prA,prB)? Beh, basta per esempio osservare che, partendo dalla coppia di morfismi idA : A ® A, k : A ® B, dove k è una qualsiasi funzione "costante" da A in B (certamente esistente nell'ipotesi B ¹ Æ), si deve allora poter costruire, in virtù delle condizioni ammesse, un unico morfismo, diciamolo pure idA´k, che va da A a Z, ed è tale che p1o(idA´k) = idA, il che basta per affermare per p1 è suriettiva (si rammenti (I.32)). Un analogo ragionamento si può fare poi per il secondo morfismo p2, cvd.

(I.84) Esiste un naturale isomorfismo canonico scambio A´B ® B´A, che trasforma la coppia ordinata (a,b) nella coppia ordinata (b,a). Esso si riduce a un automorfismo canonico scambio A´A ® A´A, quando sia A = B.

(I.85) Teorema (di rappresentazione delle azioni). Esistono due notevoli isomorfismi canonici:
H(A´B,C)  H(A,H(B,C))
H(A´B,C)  H(B,H(A,C)).

Dim. Cominciamo con il discutere il primo isomorfismo canonico. Si pensi a una funzione f da A´B verso C, e si fissi un qualsiasi elemento di A. Introdotta la fibra (prA)°(a) Í A´B, tale fibra risulta esattamente l'insieme {a}´B, il quale è evidentemente isomorfo in modo naturale a B. Restringendo la funzione f prima alla fibra su a, e componendo poi la funzione così ottenuta con il detto isomorfismo, è chiaro che si ottiene una funzione da B a C, o più precisamente una funzione da B a C che dipende dalla scelta di a. Insomma, quella che abbiamo descritto è una funzione da H(A´B,C) verso H(A,H(B,C), e non ci vuole molto per persuadersi che essa è un isomorfismo, come affermato. Ancora una volta, si tratta di situazioni che è più facile "praticare" che non descrivere. Se f(a,b) è la funzione di partenza, scritta mettendo esplicitamente in evidenza le due variabili a, b da cui essa dipende, il nostro isomorfismo è quello che trasforma la data funzione nella funzione che manda l'elemento un "generico" elemento a Î A nella  funzione da B verso C costituita esattamente da f(a,b), dove a si riguardi però come una costante. Insomma, una funzione di due variabili a, b, diciamo da A´B verso C, può essere riguardata anche come una famiglia di funzioni di una variabile, tutte da B verso C, famiglia avente come indici esattamente gli elementi di A. Per quanto riguarda il secondo isomorfismo, a parte il fatto che esso può essere introdotto e discusso esattamente come il primo, mutatis mutandis, è chiaro che esso si ottiene dal primo (così come inversamente il primo dal secondo) tramite l'isomorfismo scambio di cui al punto precedente, il quale induce anche un "ovvio" isomorfismo canonico: H(A´B,C)  H(B´A,C), sed de hoc satis. ä

Tenuto conto di quanto abbiamo anticipato, che nel caso di dominio e codominio finiti un insieme di funzioni ha una cardinalità che si esprime come una potenza, il teorema precedente esprime la circostanza che:
 = =  = .

(Con la nomenclatura dianzi introdotta, punto (I.77), il teorema (I.85) si può anche esprimere per esempio dicendo che le azioni sinistre di un insieme A su un insieme B a valori in C "equivalgono" a rappresentazioni di A in H(B,C), cioè a concepire ogni elemento di A come un morfismo da B a C. La più semplice - tautologica! - delle azioni in parola è naturalmente la funzione
V : H(A,B)´A ® B, in cui l'iniziale V ricorda il nome valutazione che si dà a codesta azione naturale. E' chiaro che si pone, con palese significato dei simboli, V(f,a) = f(a), ed è interessante cercare di capire come sia rappresentata V nell'isomorfismo canonico descritto da (I.85), ovvero come endomorfismo da H(A,B) ad H(A,B). Infatti, V è un elemento di
H(H(A,B)´A,B) @ H(H(A,B),H(A,B)) = H(H(A,B)) - usiamo qui, come già spiegato, il simbolo @ in luogo di un isomorfismo canonico - e quale elemento corrisponderà a V nell'insieme che compare alla destra della precedente relazione? Da un punto di vista squisitamente logico-naturale, trattandosi di un insieme del tipo H(X,X) = H(X), esso ammette un ben preciso elemento "eccezionale", che è idX, e invero non ci vuole molto per persuadersi che il morfismo valutazione non è altro che una delle "forme" che assume l'identità di H(A,B)!)

(Nel prossimo capitolo ci occuperemo dell'iterazione dell'operazione di prodotto cartesiano, discutendo quindi insiemi del tipo (A´B)´C, etc., in particolare quindi (A´A)´A, etc., che a rigore va ritenuto diverso dall'insieme delle terne ordinate A´A´A = H(s3,A), in quanto una coppia ordinata del tipo ((a,b),c) è diversa dalla terna ordinata (a,b,c), o dalla coppia ordinata (a,(b,c)), anche se si tratterà di notare l'esistenza di diverse possibilità di "identificazione" mediante opportuni isomorfismi canonici. Sempre in quel contesto ci occuperemo dell'estensione della nozione di prodotto cartesiano a "famiglie" eventualmente infinite di insiemi.)

Cenni sulle matrici

Nei corsi di geometria lo studente imparerà a familiarizzare con il concetto di matrice, e con la struttura algebrica che in certi insiemi matriciali si può introdurre. Ricordiamo allora che, comunque dati due numeri naturali m ed n, ed un insieme A, si dicono matrici a m righe e a n colonne sull'insieme A gli elementi dell'insieme M(m,n)(A) = H(sm´sn,A). Una matrice si dice rettangolare se m ¹ n, quadrata se m = n, nel qual caso il comune numero di righe e di colonne si dice anche l'ordine della matrice. Per l'insieme delle matrici quadrate di ordine n si usa un simbolo speciale: Mn(A).

(I.86) Nota. La distinzione in matrici rettangolari e matrici quadrate è un altro esempio di "decomposizione naturale", in questo caso nella totalità di tutte le matrici a elementi in A.

Le matrici sono dunque, come le successioni, o le k-ple ordinate, delle particolari funzioni, anche se si parla, in un senso ancora "chiaro", degli elementi di una matrice. Una matrice ha una particolare "struttura", che viene ereditata da quella particolare del suo dominio. Essa si rappresenta con una particolare convenzione di scrittura, in quella che segue indichiamo solo i posti che verranno occupati dagli elementi della matrice:

 ,

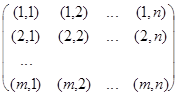uno "schema" che va interpretato nel senso che se vedo per esempio il simbolo:

 ,

con a, b, c, d Î A, allora comprendo immediatamente che si tratta della funzione f : s2´s2 ® A tale che:

f((1,1)) = a, f((1,2)) = b, f((2,1)) = c, f((2,2)) = d .

(Nella matrice quadrata in oggetto, gli elementi a, d costituiscono la diagonale principale della matrice, mentre b, c la diagonale secondaria; si tratta di semplici sottoinsiemi di A, o di qualcos'altro?)

Avrei ovviamente anche potuto scrivere, in base alle convenzioni presentate all'inizio della sezione precedente, nella forma:

 ,

oppure nella forma "equivalente":

 , etc..

L'importante è solo comprendere come la particolare "struttura" del dominio fornisce informazioni sul "posto", e quindi sul possibile ruolo, degli elementi della matrice.

Naturalmente, se si pensa allora all'uguaglianza "funzionale" riportata nella sezione precedente:

 =  ,

si comprende come essa non vada intesa nel senso che sono uguali le due matrici quadrate d'ordine 2 che in essa compaiono (come matrici ad elementi nell'insieme NÈA), ma soltanto che sono uguali le due funzioni da s2 ad A che le due matrici rispettivamente rappresentano; come dire pure che è talvolta il contesto che decide il significato di un simbolo, e le sue modalità di utilizzo.

Quando si parla di matrici, è usuale sottolineare subito l'esistenza di un morfismo naturale tra M(m,n)(A) e M(n,m)(A), che si chiama trasposizione, ed associa ad ogni matrice f : sm´sn ® A la sua trasposta, che si ottiene dalla funzione f componendola con l'isomorfismo scambio di cui al punto (I.84):
matrice trasposta = funzione composta ft : sn´sm ® sm´sn  A .
E' evidente che la trasposizione è un isomorfismo canonico tra i due insiemi di matrici specificati, il quale si riduce a un automorfismo canonico di Mn(A), naturalmente quando sia m = n .

La categoria degli insiemi

Arrivati ormai verso la fine di questo capitolo introduttivo, esprimiamo la convinzione che il modo migliore di illustrare l'intera materia in esame ci sembra quello di introdurre presto il linguaggio della teoria delle categorie, [In che misura un omaggio fuori moda a Kant da parte dei suoi fondatori? Tra di essi spicca in modo particolare il Prof. Saunders Mac Lane, tuttora vivente, che chi scrive queste pagine ha avuto l'onore di conoscere personalmente, rimanendo profondamente influenzato dalle sue chiarissime lezioni] parlando quindi della categoria degli insiemi . [Dal francese ensemble per insieme, un omaggio al contributo alla crescita della conoscenza matematica offerto dagli studiosi di quel paese nella seconda metà del secolo scorso, ma nei tempi presenti anche un segno di omaggio per il coraggio e il senso di indipendenza dalla Francia dimostrati in varie gravi occasioni; la doppia sottolineatura ha lo scopo di evidenziare la peculiarità del concetto, come si vedrà, una categoria non è un semplice insieme, ma qualcosa di più.] Una categoria è un "oggetto" complesso del pensiero che è costituito da due distinti oggetti, tra loro "interagenti". Distinguiamo pertanto gli oggetti veri e propri della categoria, la cui totalità (o "classe", termine che abbiamo detto - cfr. digressione (I.22) - potersi utilizzare quando si voglia attirare l'attenzione sul fatto che si tratta di uno di quegli "insiemi" che sono in realtà potenziali, o indeterminati, semplici "contenitori" logici) indicheremo con il simbolo auto-esplicativo Ob(), che sono nient'altro che gli insiemi (sicché, per esprimere il fatto che un certo simbolo A rappresenta un insieme, si potrà scrivere A Î Ob()), dai morfismi della categoria, che sono nient'altro che le funzioni tra insiemi, la cui totalità indicheremo con il simbolo H() (sicché, per esprimere il fatto che un certo simbolo f rappresenta una funzione, si potrà scrivere f Î H(); l'iniziale H proviene dalla circostanza che prima di morfismo in generale si era usato il termine di "omomorfismo" nella teoria dei gruppi, in inglese homomorphism, appunto; si ricordi peraltro che noi abbiamo usato la stessa locuzione per parlare delle "immagini omomorfe" di un dato insieme A). L'interazione tra Ob() e H(), i quali sono due classi assolutamente disgiunte (un insieme non è una funzione, e una funzione non è un insieme), rimane stabilita dal fatto che ogni morfismo (funzione) ammette un ben preciso dominio e codominio, cioè che esistono due "funzioni" (le virgolette cercano di mettere enfasi sul fatto che i rispettivi domini e codomini di queste funzioni sono classi assai generali):
dom: H() ® Ob(), codom: H() ® Ob(),
le quali si possono tra loro comporre in un'unica funzione di incidenza:
I : H() ® Ob()´Ob(),
la quale associa ad ogni morfismo f la coppia ordinata di oggetti della categoria, (dom(f),codom(f)) (anche in questo caso, non c'è alcuna difficoltà a introdurre la classe di tutte le funzioni da s2 verso Ob(), le quali non sono comunque morfismi della categoria , perché se hanno come dominio un insieme, ovvero s2 Î Ob(), il loro codominio non deve considerarsi un insieme, non potendo concepirsi l'appartenenza auto-referenziale Ob() Î Ob()).
Assegnata allora una qualsiasi coppia ordinata (A,B) Î Ob()´Ob(), il pull-back I°(A,B) costituisce un sottoinsieme di H(), che è proprio quello che abbiamo chiamato H(A,B): I°(A,B) = H(A,B) (si noti che sono entrambe corrette le scritture: I°(A,B) Í H(), I°(A,B) Î Ob()).
Quando si vuole pensare alla categoria , o più in generale, come vedremo, a una qualsiasi categoria, conviene pensare a qualcosa che si è cercato di rendere visivamente nel seguente disegno, dove gli oggetti della categoria sono rappresentati come punti, e i morfismi come frecce, o vettori, che collegano tra loro i punti (ogni freccia ha un ben preciso estremo = punto iniziale e un ben preciso estremo = punto finale). Tutte le frecce tra due punti A e B costituiscono precisamente l'insieme H(A,B), che a sua volta è rappresentato da qualche punto:

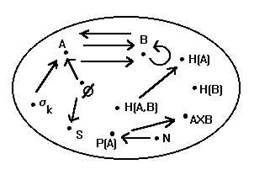
(Fig. I.87)
(Un'immagine mentale della categoria degli insiemi ;
una freccia "circolare" come quella che va da B a B
rappresenta un endomorfismo di B, e si dice anche,
con il linguaggio della teoria dei grafi, a cui quella delle categorie
è come vedremo collegata, un self-loop)

La categoria degli insiemi è dunque costituita da due classi di oggetti, che sono gli insiemi e le funzioni, tra loro collegate da una funzione di incidenza, ma c'è di più, abbiamo visto che in H() è naturalmente presente una struttura algebrica di semigruppo "largamente unitario", ma su tutto ciò torneremo nel capitolo VI, quando cercheremo di dare, a partire dall'esempio fondamentale di , ma non solo, una definizione generale di categoria.

Per il momento limitiamoci, dopo tanta "generalità", a ritornare a dare qualche esempio di funzioni notevoli, studiando in particolare il caso di quegli insiemi di morfismi H(A,B) per i quali o A o B sono "piccoli".
Già abbiamo esaminato il caso del dominio vuoto: l'insieme H(Æ,B) è sempre un singleton, per qualsiasi elemento B Î Ob(), e la circostanza si esprime, con linguaggio al solito espressivo, affermando che l'insieme vuoto è un elemento iniziale della categoria , ovvero, ripetiamolo, esiste uno ed un solo morfismo che collega il vuoto ad un altro insieme B, come abbiamo cercato di rappresentare nella seguente figura:

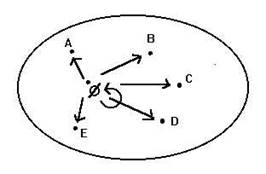
(Fig. I.88)
(Il vuoto come elemento iniziale di )

Conosciamo pure il caso degli insiemi H(A,Æ), che sono viceversa sempre vuoti, tranne nel caso appunto che pure A sia vuoto, e passiamo quindi a esaminare il caso che il dominio A dell'insieme di funzioni H(A,B) sia un singleton (abbiamo due candidature per un singleton "canonico": s1 = {1}, o quello che abbiamo chiamato, cfr. punto (I.3), K, K ={Æ}, il singleton del vuoto, ma è ben immaginabile dove vanno le nostre personali preferenze!). Abbiamo già visto (punto (I.71)) come sia fatto H(s1,A), per qualsiasi insieme A, e passiamo quindi al caso in cui s1 appaia come codominio in un insieme H(A,B). Ci si rende immediatamente conto che H(A, s1) è sempre un singleton, qualunque sia A (compreso il caso A = Æ), e la circostanza si esprime allora dicendo che i singleton (ce ne sono tanti) sono elementi finali della categoria , nel senso che esiste uno ed un solo morfismo che collega un qualsiasi insieme a un singleton S, come abbiamo cercato di rappresentare nella seguente figura:

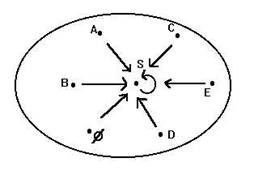
(Fig. I.89)
(Un singleton come elemento finale di )

Riassumiamo, in  c'è un unico elemento iniziale, che è il vuoto, e ci sono "tanti" elementi finali, tutti ovviamente però isomorfi tra di loro (e diversi dall'elemento iniziale). [Tra due singleton esiste anzi un unico isomorfismo, che è quindi per forza di cose "canonico", una circostanza che, seppur molto più banale, in qualche modo assomiglia logicamente a quella che abbiamo già incontrato quando si discuteva della proprietà universale di un prodotto cartesiano. Nel presente caso, infatti, poiché esiste un unico morfismo da un qualsiasi insieme A a un dato singleton S, se S' è un "altro" singleton, diverso o no da S, allora esistono un unico morfismo a da S' ad S, ed un unico morfismo b da S ad S', con la conseguenza che aob non può che essere l'identità di S, allo stesso modo che boa non può che essere l'identità di S'.]

Passando ora al caso successivo, ricordiamo che la presenza di s2 come dominio di H(A,B) la abbiamo pure già investigata, quando abbiamo introdotto la "potenza cartesiana" B2 esattamente come l'insieme H(s2,A). Ci resta pertanto solo da esaminare il caso H(A,s2), che resterà descritto da un importante teorema, al quale premettiamo però alcune considerazioni generali sui rapporti tra il concetto di insieme e quello di funzione. In effetti, adesso che conosciamo una definizione precisa di prodotto cartesiano, possiamo discutere in maniera adeguata perché la definizione di funzione va intesa come primitiva, nonostante alcuni amino presentarla come un insieme (per eccesso di riduzionismo). In effetti, data una qualsiasi funzione f : A ® B, è possibile associare ad essa un particolare sottoinsieme di A´B, che si dice il grafico di f, e che indicheremo con il simbolo Gf . Il grafico di f è, come lo studente è peraltro abituato a conoscere dai suoi primi studi di matematica, l'insieme delle coppie ordinate (x,f(x)), ovvero Gf = {" (a,b) Î A´B ½ ($ x Î A : (a = x)Ù(b = f(x))}. E' chiaro che la funzione G : H(A,B) ® P(A´B) definita mediante la posizione G(f) = Gf è una rappresentazione fedele del dominio nel codominio, in quanto funzioni diverse hanno manifestamente grafici diversi. Dato un graficoGf, la funzione f da cui esso proviene si ricostruisce in modo "immediato" attraverso l'identità:
f(a) = prB(prA°(a)ÇGf), nella quale bisogna fare però attenzione al fatto che l'insieme che compare tra parentesi tonde è per ipotesi un singleton, e che per abuso di notazione si è indicato con il "nome" dell'insieme quell'unico elemento da cui esso è costituito, e del resto solo ad elementi di A´B è possibile "applicare" la proiezione prB. Allora, se prendiamo Im(G), ecco che abbiamo un insieme di insiemi (sottoinsiemi particolari di A´B), il quale risulta isomorfo in modo naturale al nostro insieme di funzioni H(A,B), d'onda la tentazione di dire che una funzione tra A e B è precisamente un elemento di Im(G), un insieme che a sua volta si può "caratterizzare" facilmente indipendentemente dall'esistenza della rappresentazione G, la quale presuppone ovviamente la conoscenza di H(A,B) (la caratterizzazione in parola è quella già evidenziata: per ogni elemento a Î A, il pull-back prA°(a) deve unisecare un dato sottoinsieme di A´B perché esso possa dirsi una "funzione" tra A e B; il "trasformato" di a sarebbe di conseguenza quell'unico elemento b Î B tale che il singleton in oggetto sia esattamente {(a,b)}). Dicevamo di una "tentazione", perché se è vero che un ismorfismo naturale consente di "identificare" due insiemi da esso collegati, ovvero due "concetti" che in tali insiemi si "sostanziano", ecco che per poter tramutare le funzioni in insiemi bisogna comunque conoscere almeno il prodotto cartesiano A´B, e questo è per noi collegato al concetto di funzione, sicché saremmo in presenza solo di un'apparente scomparsa delle funzioni, che in qualche misura (ancorché limitata) resterebbero nel concetto di "coppia ordinata", qualora questo si volesse considerare "primitivo" (e comunque sempre a due intuizioni primitive bisognerebbe fare ricorso: o insiemi e funzioni, come noi suggeriamo, o insiemi e coppie ordinate). [Corre l'obbligo di informare che, per evitare siffatte obiezioni, è stata proposta la seguente definizione strettamente insiemistica di coppia ordinata di due elementi a, b: (a,b) = {a, {a,b}}, almeno se a ¹ b (se invece a = b, si pone coerentemente
(a,b) = {a, {a}}). E' chiaro in che senso l'insieme (gli insiemi) specificato(i) corrispondano al concetto intuitivo di coppia ordinata, ma manteniamo l'opinione che la definizione insiemistica appena introdotta non ne sia una descrizione "adeguata".]

(I.90) Nota. L'appena discussa circostanza porta alcuni a introdurre un concetto generale di "funzione" tra due insiemi A e B, come un qualsiasi sottoinsieme del prodotto cartesiano A´B, e si tratterebbe quindi di "funzioni" che dovrebbero dirsi multivoche, e non univoche quali quelle che abbiamo qui considerato, e sempre considereremo. A siffatte "funzioni multivoche", che non saranno poi in sostanza altro che le nostre ordinarie funzioni da A verso P(B), pur assai significative, preferiamo dare un altro nome, quello di relazione tra A e B, ma di ciò discuteremo nel III capitolo, dimostrando pure in che senso l'insieme delle relazioni tra A e B (che indicheremo con il simbolo Rel(A,B), e sarà appunto, per nostra precisa definizione!, coincidente con l'insieme H(A,P(B)), si possa naturalmente identificare con l'insieme P(A´B), il che chiuderà in maniera definitiva il "cerchio" logico in cui ci stiamo dibattendo.

Dopo questo lungo excursus, mirante ad illustrare la circostanza che le funzioni sono comunque descrivibili mediante insiemi, ecco che possiamo tornare alla nostra questione primitiva, e cioè lo studio degli insiemi H(A,s2), un'investigazione che, a sorpresa o no, ci mostrerà che, viceversa, gli insiemi sono descrivibili mediante funzioni (ma nessuno pensa per questo di ridurre il concetto di insieme a quello di funzione, laddove abbiamo detto è al contrario frequente tentare il viceversa!). Riassumendo, saremo così condotti a comprendere che insiemi e funzioni sono collegati in modo profondo, seppur in un modo non atto a consentire il riduzionismo di un concetto all'altro (ripetiamo, bisogna comunque conoscere il concetto di insieme prima di quello di funzione, mentre ridurre le funzioni a insiemi non ci sembra soprattutto "opportuno"). Il "fatto" matematico a cui ci stiamo riferendo è il contenuto del seguente, facile ma importante:

(I.91) Teorema. Esiste un isomorfismo canonico F tra l'insieme delle parti di un qualsiasi insieme A, e l'insieme H(A,s2), i cui elementi si dicono le funzioni caratteristiche di A, F : P(A)  H(A,s2) .

Dim. Il teorema si illustra subito "a parole" evidenziando il fatto che, comunque dato un sottoinsieme X Í A, è lecito descrivere l'appartenenza di un elemento "generico" a Î A ad X come se si trattasse, invece che di un insieme (sottoinsieme di A), appunto di una particolare funzione, avente come dominio l'intero A, e come output, o "valori", le affermazioni SI' o NO, VERO o FALSO, o anche 1 o 2 (questa è la specificazione del codominio della funzione). Una funzione che interviene nel rispondere a tutte le domande: a appartiene ad X? sì, valore della funzione che stiamo cercando di definire uguale ad 1, oppure no, valore della funzione che stiamo cercando di definire uguale a 2. E' chiaro del resto che l'"insieme" di tutte queste risposte corrisponde alla conoscenza precisa del sottoinsieme X. Un esempio concreto varrebbe più di mille parole, e lo studente potrebbe elaborare per esempio l'isomorfismo in questione in un caso semplice, scegliendo un "piccolo" A, tanto per dire A = s3. In un modo più "formale" (soddisfacente il gusto matematico della nostra epoca), " X Î P(A) si introduce una funzione caratteristica fX del sottoinsieme X, fX Î H(A,s2), la quale resta definita attraverso la seguente "regola":
" a Î A, fX(a) = 1 Û a Î X ; fX(a) = 2 Û a Ï X Û a Î CA(X)
(l'ultima osservazione fa comprendere anche come la funzione caratteristica di CA(X) si ottenga da quella di X sostituendo tutti gli 1 con 2, e tutti i 2 con 1).
E' assolutamente diretto (in questi casi gli inglesi dicono straightforward) dimostrare che, se X ¹ Y, allora fX ¹ fY (la corrispondenza F risulta cioè iniettiva), e che, comunque data una funzione f Î H(A,s2), è possibile determinare un sottoinsieme X Í A (in effetti uno ed uno solo), tale che risulti:
f = fX, ossia f = F(f). Entrambe le asserzioni sono così evidenti che non ci sarebbe bisogno di aggiungere altro, ma in un corso per principianti conviene forse discuterle un poco, così per "esercizio" di logica.
Per quanto riguarda l'iniettività di F:
X ¹ Y Þ [$ a Î A ½ ((a Î X)Ù(a Ï Y))Ú((a Î Y)Ù(a Ï X))] Þ
Þ [((fX(a) = 1)Ù(fY(a) = 2))Ú((fY(a) = 1)Ù(fX(a) = 2))] Þ fX ¹ fY .
Per quanto riguarda la suriettività di F:
" f Î H(A,s2), X = f°(1) (si rammenti (I.24)) Þ f = fX . ä

Del "teorema delle funzioni caratteristiche" daremo qualche importante applicazione sia quando parleremo di "aritmetica transfinita" (II teorema di Cantor), sia all'inizio del capitolo III, quando torneremo sull'importante concetto di relazione, e sulla importante identificazione tra H(A,P(B)) e P(A´B), che avverrà attraverso i teoremi (I.85) e (I.91).

Congedo

Insiemi e funzioni, ai quali abbiamo dedicato questo primo ampio capitolo base dell'algebra, sono i "mattoni" con i quali si costruisce l'intero edificio matematico. In ogni momento, di fronte a un ente matematico complesso, si deve SEMPRE poter rispondere alla domanda: "che cos'è?", e le risposte non potranno che essere del tipo: è quel certo insieme, o: è quella certa funzione. Le domande potranno poi eventualmente susseguirsi come le famose ciliegie, in un procedimento di analisi regressiva comunque limitato, potendosi infatti chiedere, qualora trattisi di una funzione, "e chi è il suo dominio?", "e chi è il suo codominio?", oppure, qualora trattisi invece di un insieme, "chi sono i suoi elementi?", alla quale domanda bisognerà di nuovo saper rispondere nel senso che si tratterà o di insiemi o di funzioni, e così via, fino ad arrivare al livello primitivo da cui tutto comunque deve aver preso le mosse, per esempio quindi da OGGETTI, che possono essere numeri, punti, etc., vedi quanto è stato detto sul concetto di "universo".

Di tutto ciò diremo sempre meglio, si spera, e sempre meglio ne avrà comprensione lo studente, quanto più volgerà la sua navigazione in mare aperto. Noi saremo lieti se queste pagine saranno state capaci di dargli un'idea di come possa (debba!) essere sviluppata la matematica in maniera "moderna" (ma che avrebbe potuto altrettanto bene essere "antica", si veda l'epigrafe al capitolo IV). Noi non possiamo augurargli altro che la navigazione gli sia "leggera", cosa che senz'altro avverrà nella misura in cui egli si sarà convenientemente attrezzato ad affrontarla.

Chiudiamo (fatta salva l'appendice) questa prima tappa di un itinerario che si farà sempre più avvincente, per coloro che resisteranno alla tentazione della "pigrizia intellettuale", riportando in fine, e non in principio, il lungo brano che abbiamo prescelto come "epigrafe" al presente capitolo. Esso ci perviene, ancora attualissimo, da una distanza di secoli, a riprova che, sostanzialmente, per l'uomo: <<Ciò che è stato sarà e ciò che si è fatto si rifarà; non c'è niente di nuovo sotto il sole>> (Ecclesiaste, 1,9). Lo offriamo all'attenzione dei lettori perché ci sembra che costituisca uno degli elogi più profondi che siano mai stati concepiti in onore della matematica, e del suo ruolo nella fondazione di ogni "conoscenza".

<<Ora tutto ciò che è frammentario è un intralcio a un ripiegamento in se stessi, e tutto ciò che crea forme illusorie turba la conoscenza pura, e ogni passionalità è impedimento alla sua impassibile attività. Quando dunque si riesca a rimuovere questi intralci dalla conoscenza ragionata, allora potremo conoscere i concetti che essa ha in se stessa, ed essere effettivamente istruiti e produrre di essa una conoscenza sostanziale. Ma prigionieri come siamo, e chiusi l'occhio dell'anima, giammai potremo ottenere la perfezione che ci converrebbe. Questa è dunque la mathesis: reminiscenza delle idee eterne che sono nell'anima; ed essa è il motivo per cui lo studio che ci soccorre egregiamente per la reminiscenza di quelle idee ha preso il nome di matematica. E in che cosa consiste la funzione di questa scienza è rivelato dal suo nome stesso; cioè essa mette in moto la nostra conoscenza innata, risveglia l'Intelletto, purifica la riflessione, mette in luce i concetti che sono in noi in essenza, cancella l'oblio e l'ignoranza che abbiamo dalla nascita, scioglie i legami derivanti dall'irrazionalità>> (Proclo, Commento al I Libro degli Elementi di Euclide, Prologo, Parte I).

 

Appendice - Approfondimento della struttura algebrica di H()

 

La teoria kantiana delle categorie <<tutto sacrifica a un furore simmetrico>> (Arthur Schopenhauer).

Possibilità di cancellazione

Ancorché si tratti soltanto di un semigruppo parziale, [Ma largamente unitario, nel senso che " A Î Ob(), esiste un morfismo idA in H(A), il quale funge non solo da elemento neutro per il semigruppo H(A) (e in quanto tale è quindi unico come abbiamo già visto), ma anche da elemento neutro per ogni composizione ammissibile foidA = f, idAof = f. Nel primo caso, f deve essere un morfismo con dominio A; nel secondo, con codominio A.] è possibile discutere alcune proprietà algebriche generali di H(), simili a quelle che abbiamo esaminato nella sezione dedicata alle "Caratterizzazioni algebriche della qualità di un morfismo". Si tratta di questioni che possono approfondirsi nel caso di un qualsiasi altro semigruppo, come può essere N, con l'operazione tanto di somma, quanto di prodotto, [E questi sono semigruppi molto diversi tra loro, il secondo per esempio è unitario, il primo no. Sarebbe invece tale N0, con la struttura che si dice additiva (e quindi la sua "unità" diventa lo "zero"), ma anche N, con la struttura moltiplicativa, e N0, con la detta struttura additiva, risultano non isomorfi, come vedremo nel capitolo VI.] oppure, per ogni insieme A, l'insieme delle parti P(A), vuoi con l'operazione di unione, vuoi con quella di intersezione. Si rammenti che l'unica condizione richiesta per l'operazione di un semigruppo è che sussista la proprietà associativa; la circostanza che le operazioni appena nominate siano anche commutative è puramente accidentale (ovviamente benvengano ulteriori proprietà "comode", quando esse ci sono!). Semigruppi siffatti si dicono commutativi, o abeliani (in onore del matematico norvegese Niels Henrik Abel, 1802-1829, scomparso quindi giovanissimo), ma come abbiamo già avuto modo di osservare nel corso di questo primo capitolo, e preciseremo definitivamente nel secondo (teorema (II.18)), i semigruppi del tipo H(A) per esempio sono eminentemente non commutativi. Sottolineiamo in modo esplicito tale circostanza perché in un ambito non commutativo saremo chiamati qui a operare a proposito di morfismi di .

Cominciamo analizzando la possibilità di cancellazione, o semiregolarità, destra o sinistra, di un morfismo. Dato un diagramma (peraltro arbitrario) del tipo rappresentato nella seguente figura:

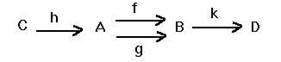
(Fig. I.A.1)
(Il diagramma da cui si parte per studiare la semiregolarità di certi morfismi)

consideriamo le due coppie di morfismi foh, goh (da C verso A), e le due coppie di morfismi kof, kog (da A verso D). Diremo che h è cancellabile a destra, o semiregolare a destra (ma si noti che invero h compare alla sinistra nella precedente figura, per motivi che abbiamo chiarito quando si è parlato di prodotto operatorio tra funzioni), se tutte le volte che si verifica l'identità
foh = goh, da essa consegue che f = g. Diremo invece che h è cancellabile a sinistra, o semiregolare a sinistra, se analogamente: kof = kog Þ f = g.

(I.A.2) Nota. Un qualsiasi semigruppo si dice semiregolare a destra se tutti i suoi elementi sono semiregolari a destra; si dice semiregolare a sinistra se tutti i suoi elementi sono semiregolari a sinistra. Si dice regolare tout court, se è semiregolare tanto a destra quanto a sinistra. Manifestamente, (N,+) e (N,*) (così scriveremo un semigruppo, mettendo in evidenza l'operazione che lo costituisce, nel primo caso l'ordinaria somma tra numeri naturali, nel secondo caso il prodotto, qui denotato con il simbolo *) sono semigruppi regolari (si noti che la distinzione tra destra e sinistra adesso non si pone, perché si ha a che fare con semigruppi abeliani). Vedremo esempi di non regolarità sia nel corso dell'attuale discussione, sia nel capitolo dedicato all'aritmetica transfinita, e lo studente ne incontrerà ancora numerosi, quando studierà in altri corsi il prodotto righe per colonne tra matrici quadrate dello stesso ordine a coefficienti per esempio in un campo (un'operazione di cui in questo corso non ci occuperemo se non di sfuggita, e che comunque si ricollega al prodotto operatorio tra funzioni).

Posto il problema, iniziamo a notare che esistono morfismi certamente non semiregolari, né a destra, né a sinistra, approfittando dell'occasione per introdurre il concetto di zeri di un semigruppo, che esso sia parziale come H() oppure no. Nel nostro caso generale, zeri sono quei morfismi z tali che, moltiplicati per un qualsiasi altro morfismo f (laddove si possa), effettuato cioè il prodotto zof, o foz, restano uguali a se stessi: zof = z, foz = z, o più precisamente di zeri sinistri se vale la prima identità, e di zeri destri se vale la seconda (al solito, l'espressione non esclude in entrambi i casi che possa sussistere anche l'altra circostanza, cioè che si tratti di uno zero tout court, che allora si dice anche uno zero bilatero).

L'origine della nomenclatura è ben chiara, dal momento che " x Î N0, risulta: 0*x = 0, circostanza che si esprime, con la nomenclatura appena introdotta, asserendo che lo 0 è uno zero del semigruppo moltiplicativo (N0,*), anzi l'unico zero di tale semigruppo. Ben chiara è pure la connessione con la questione della cancellabilità, appunto perché lo 0 di N0 non è cancellabile, in quanto per esempio 0*1 = 0*2 = 0, ma 1 ¹ 2, ed è anzi l'unico elemento non cancellabile (o non regolare) di tale palesemente notevole semigruppo moltiplicativo. Si noti che 0 è uno zero (attenzione al "bisticcio" di parole!) unicamente per la struttura di semigruppo moltiplicativo dell'insieme dei numeri cardinali finiti; la specificazione è d'obbligo, perché lo stesso elemento funge invece da elemento neutro, o "unità", per la struttura additiva definita sul medesimo insieme dall'operazione di somma (naturalmente, si potrebbero discutere anche eventuali zeri del semigruppo (N0,+), ossia "numeri" z tali che z + x = z per ogni altro numero x, che però non esistono), come a dire che l'intera discussione presenta qualche rischio di equivoco qualora con il simbolo "0", e con il termine "zero", si indichi appunto, come tradizionale, l'eventuale elemento neutro di un arbitrario semigruppo scritto in forma additiva (convenzione che del resto si usa generalmente solo in un contesto abeliano, per evitare cattive suggestioni, però con qualche significativa eccezione, come la "somma" di numeri ordinali, di cui si parla negli Elementi...).

Dopo queste brevi considerazioni introduttive, determiniamo qualche piccolo teorema generale. Intanto, l'unicità dello zero di (N0,*) è una conseguenza generale della definizione di zero (bilatero) di un qualsiasi semigruppo (S,*) (usiamo lo stesso simbolo * anche per l'operazione di S). Infatti, se un certo elemento z fosse uno zero di tale semigruppo, e z' fosse un "altro" zero del medesimo semigruppo, dalle relazioni necessarie: zoz' = z (poiché z è in particolare zero sinistro), zoz' = z' (poiché z' è in particolare zero destro), si deduce appunto z = z'. Tale ovvietà mostra anche che, se pure uno zero destro non è necessariamente sinistro (e vedremo nel capitolo VI casi in cui tale distinzione teorica si presenta effettivamente), e pertanto non necessariamente uno zero bilatero, non possono comunque esistere "contemporaneamente" in un semigruppo uno zero destro e uno zero sinistro distinti, perché allora essi dovrebbero necessariamente coincidere in un unico elemento, che sarebbe uno zero (bilatero) tout court. Inoltre, notiamo pure che, fatta eccezione al solito per il semigruppo vuoto, che possiamo considerare regolare per mancanza di condizioni da verificare, e per il caso di un insieme S che sia un singleton, il cui unico elemento funge allora allo stesso tempo da unità e da zero (e si tratta allora ancora di un semigruppo regolare), in un semigruppo (S,*) "generale" l'eventuale unità u non può mai essere uno zero, né destro né sinistro (perché,
" x Î S, il prodotto x*u risulta uguale a x, e non a u), e gli eventuali zeri, vuoi destri che sinistri, non possono essere mai cancellabili (perché per esempio
x*z = z*z = z, e potrebbe essere x ¹ z, se S ha almeno due elementi).

Date tali premesse, torniamo al semigruppo parziale H() (sottinteso, ovviamente, rispetto al prodotto operatorio), cercando di determinare suoi eventuali zeri (laterali), che ci aspettiamo non cancellabili. Notiamo prima di tutto che dalla foz = z, con z : A ® B, e f : B ® C, poiché z Î H(A,B), e
foz Î H(A,C), si deduce intanto che deve essere necessariamente B = C, con la conseguenza che, esistendo certamente morfismi del tipo f: B ® C, con B ¹ C, ai quali applicare la specificata proprietà di zero (destro) per z, semplicemente non esistono zeri destri in H(). Una conclusione analogo si raggiunge per la ricerca degli zeri sinistri. Infatti, ferma restando la z : A ® B, da un'eventuale identità zof = z, si deduce prima di tutto che f deve essere del tipo f: C ® A, per qualche insieme C, e che quindi dovrebbe risultare A = C, poiché z Î H(A,B), e zof Î H(C,B). Anche adesso, esistendo certamente morfismi del tipo f: C ® A, con C ¹ A, ai quali applicare la specificata proprietà di zero (sinistro) per z, si conclude che non esistono neppure zeri sinistri in H().

E allora, stiamo facendo un discorso "astratto" completamente inutile? Non del tutto, perché possiamo restringere l'indagine alla ricerca di eventuali zeri (laterali) dei sottosemigruppi (H(A),o) di (H(),o) (adesso abbiamo specificato l'operazione di cui trattasi, anche nel caso in cui si ha a che fare con un semigruppo solo parziale), per un arbitrario insieme A, fatta eccezione al solito per l'insieme vuoto e i singleton, per i quali H(A) risulta un singleton, un caso che abbiamo già esaminato. Dunque, se si cercano adesso morfismi
z Î H(A), tali che foz = z, per ogni morfismo fÎ H(A), è chiaro che non se ne trovano, dal momento che, fissato un arbitrario elemento a Î A, e dato quindi z(a), basta scegliere un elemento b ¹ z(a) in A, e un morfismo f tale che
f(z(a)) = b (per esempio il morfismo costante kb, " x Î A Þ kb(x) = b, si rammenti (I.29)), per avere appunto che foz(a) = b ¹ z(a). Diversa è invece la questione degli zeri sinistri, zof = z. E' chiaro infatti che proprio i morfismi costanti kb di poc'anzi sono degli zeri sinistri, poiché:
" x Î A Þ (kbof)(x) = b = kb(x). E' facile convincersi poi che questi sono gli unici zeri sinistri di (H(A),o), [Poiché, se per un dato morfismo f Î H(A), esistono due elementi x, y Î A, x ¹ y, tali che f(x) ¹ f(y) - cioè, f non è costante - allora, introdotto l'endomorfismo s di A che "scambia" tra loro x e y, lasciando tutti gli altri elementi fissi, risulta (fos) ¹ f, dal momento che appunto (fos)(x) = f(y) ¹ f(x).] e che sono tutti elementi manifestamente non cancellabili (in H(A), e quindi a maggior ragione, a fortiori, in H(): per esempio, kboidA = kbokb, con idA ¹ kb), sicché possiamo concludere che sussiste il seguente (piccolo):

(I.A.3) Teorema. Nelle attuali ipotesi (A con almeno due elementi), il semigruppo (H(A),o) ha zeri sinistri, che sono gli elementi dell'insieme Im(cA) (si rammenti (I.29)); non ha zeri destri (in particolare non ha uno zero bilatero); non è semiregolare a sinistra (in particolare non è regolare).

Del resto, (H(A),o) non è neppure semiregolare a destra, come si comprende subito introducendo un altro concetto di particolare interesse nella teoria dei semigruppi, quello di idempotente. Un morfismo f Î H() si dice idempotente se f2 = fof = f, allo stesso modo che un elemento x di un semigruppo (S,*) si dice idempotente se x2 = x*x = x. Nel caso di un morfismo
f : A ® B, si capisce subito che: 1 - f2 si può fare soltanto se A = B, ovvero se f è elemento di qualche H(A); 2 - un morfismo idempotente non banale, ossia diverso dall'endomorfismo identità, è certamente non cancellabile, né a destra né a sinistra, perché f = fof = foidA = idAof, e appunto f ¹ idA.

[Esercizio. Sia f : A ® B un qualsiasi morfismo tra due insiemi A e B assegnati ad arbitrio che risulti invertibile a destra, ovvero sia tale che $ g : B ® A, con fog = idB. Sappiamo che, se f è invertibile pure a sinistra, hof = idA, con palese significato dei simboli, allora h = g, ed f è un isomorfismo tra A e B. Ma in generale quanto fa gof? Si osservi che gf (eliminiamo adesso il simbolo esplicito di prodotto) è comunque un idempotente di H(A), e che se non è l'elemento neutro di tale semigruppo, pure esso funge da unità destra per f: f(gf) = f, ma non necessariamente sinistra (a meno che appunto f non sia invertibile tout court).]

Esclusi i soliti casi limite, la dimostrazione della non semiregolarità destra dei semigruppi H(A) (con un leggero abuso di notazione) può essere conseguita allora come corollario dell'esistenza di idempotenti non banali in H(A), tra cui, si noti subito, vi sono certamente i morfismi costanti (i quali quindi, pur non essendo zeri destri, risultano comunque non cancellabili nemmeno a destra).

E se volessimo determinare tutti gli idempotenti di H(A)? (supposto ancora che A possegga almeno due elementi). Si comprende subito che la condizione
f2(x) = f(x), per ogni elemento x Î A, equivale alla condizione che l'endomorfismo f, ristretto alla propria immagine Im(f), coincide con idIm(f) (in generale, comunque dato un endomorfismo f, la restrizione f½Im(f) è un morfismo da Im(f) ad A, il quale si può considerare, mediante un'altra ovvia restrizione, ma questa volta di codominio, come un endomorfismo di Im(f)). Tale semplice osservazione permette di comprendere immediatamente come si possano costruire tutti gli idempotenti di H(A). Assegnato un qualsiasi sottoinsieme non vuoto X Í A, si prende un endomorfismo f di A che risulti così costruito: sugli elementi x di X, f(x) vale x; sugli elementi x di A non in X, f(x) vale un elemento arbitrario di X; ossia, f coincide (a meno di una restrizione di codominio) con quella che abbiamo detto una retrazione dell'inclusione canonica X  A. Raccogliamo esplicitamente il risultato formulando il seguente:

(I.A.4) Teorema. Gli idempotenti di H(A) sono tutte e sole le retrazioni delle inclusioni canoniche X  A, al variare di X ¹ Æ nell'insieme delle parti di A, moltiplicate per la relativa inclusione canonica.

Insomma, abbiamo visto finora che, tra zeri e idempotenti, i semigruppi H(A) sono (in generale) altamente non semiregolari (a fortiori non regolari), ma è tempo ormai di affrontare la questione generale della cancellabilità di un morfismo in H(), a cui questa sezione è precipuamente dedicata (nonostante ne abbiamo approfittato per offrire qualche esempio di "algebra" dei semigruppi). Ripartiamo dunque dalle:

(I.A.5) foh = goh Þ? f = g.
(I.A.5') kof = kog Þ? f = g.

E' manifesto che, se h è invertibile a destra, oppure se k è invertibile a sinistra, allora la discussa cancellazione si può effettuare. Nel primo caso infatti esisterà qualche morfismo h' Î H(A,C) tale che hoh' = idA, sicché:

foh = goh Þ (foh)oh' = (goh)oh' Þ fo(hoh') = go(hoh') Þ foidA = goidA Þ f = g

(si noti l'essenzialità della proprietà associativa per siffatti tipi di calcoli),

e analogamente nell'altro caso, $ k' Î H(D,B) tale che k'ok = idB.

Raccogliamo esplicitamente il risultato:

(I.A.6) Teorema. Ogni morfismo h invertibile a destra è cancellabile, ossia semiregolare, a destra. Ogni morfismo k invertibile a sinistra è cancellabile, ossia semiregolare, a sinistra.

(I.A.7) Corollario. Tutti i gruppi sono in particolare semigruppi regolari.

Combinando adesso (I.32') con (I.A.6) otteniamo:

(I.A.8) Teorema. Un qualsiasi epimorfismo h : C  A è semiregolare a destra.

Combinando invece (I.31') con (I.A.6) otteniamo:

(I.A.9) Teorema. Un qualsiasi monomorfismo k : B  D è semiregolare a sinistra.

(Si noti che (I.A.9) vale banalmente anche se B = Æ, un caso che era invece eccezionale per (I.31')).

Ricordando il teorema (I.26), si ottengono subito i seguenti corollari dei teoremi (I.A.8) e (I.A.9), rispettivamente:

(I.A.10) Corollario. Per ogni insieme A, (Epi(A),o) è un sottosemigruppo di (H(A),o) regolare a destra (se A è finito, risulta addirittura Mono(A) = Aut(A), sicché in questo caso l'affermazione sarebbe conseguenza del solo corollario (I.A.7)).

(I.A.11) Corollario. Per ogni insieme A, (Mono(A),o) è un sottosemigruppo di (H(A),o) regolare a sinistra (se A è finito, risulta addirittura Mono(A) = Aut(A), sicché in questo caso l'affermazione sarebbe conseguenza del solo corollario (I.A.7)).

I due teoremi (I.A.8) e (I.A.9) si possono anche facilmente invertire:

(I.A.8') Teorema. Ogni morfismo h : C ® A semiregolare a destra (in H()) è necessariamente un epimorfismo (e quindi semiregolarità destra e suriettività sono la stessa cosa).

Dim. Sia infatti h un morfismo da C ad A tale che Im(h) Ì A, e sia f il morfismo costante f da A a s2 che manda tutti gli elementi di A (certamente diverso dal vuoto) in 1. Sia invece g il morfismo di medesimi dominio e codominio che manda tutti gli elementi di A - Im(h) in 2, e quelli di Im(h) in 1 (se Im(h) = Æ, e quindi C = Æ, tale specificazione diventa vuota, e g sarà il morfismo costante da A a s2 che manda tutti gli elementi di A in 2). E' chiaro che in ogni caso f ¹ g, mentre fh = gh (si tratta del morfismo costante che manda tutti gli elementi di C in 1, oppure l'inclusione canonica del vuoto in s2), qed. ä

(I.A.9') Teorema. Ogni morfismo k : B ® D semiregolare a sinistra (in H()) è necessariamente un monomorfismo (e quindi semiregolarità sinistra e iniettività sono la stessa cosa).

Dim. Proviamo che se k non è un monomorfismo allora esso non può essere cancellabile a sinistra. Per ipotesi $ x, y Î B, x ¹ y, tali che k(x) = k(y), e quindi possiamo introdurre due morfismi f, g da s2 a B con le seguenti posizioni:
f(1) = x, f(2) = y; g(1) = y, g(2) = x. E' palese che risulta attualmente f ¹ g, mentre kf = kg, qed. ä

I due ultimi teoremi caratterizzano monomorfismi ed epimorfismi in termini di semiregolarità "un po' meglio" di quanto non sia possibile fare tramite la condizione di invertibilità laterale.

Equazioni di I grado nel semigruppo parziale H()

Riprendiamo adesso la questione generale delle estensioni-restrizioni di un qualsiasi morfismo f : A ® B, un problema che equivale alla discussione di quelle che potremmo dire le equazioni di I grado nel semigruppo parziale H().

Cominciamo da lontano, ritornando sulle già discusse restrizioni di dominio ed estensioni di codominio, due situazioni banali che illustreremo adesso, rispettivamente, con i seguenti diagrammi, relativi ai casi più semplici in cui si presentano tali concetti:

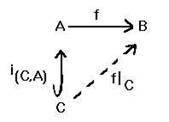
(Fig. I.A.12)
(Restrizioni di dominio "in senso stretto")

 

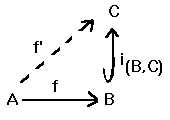
(Fig. I.A.13)
(Estensioni di codominio "in senso stretto")

(Si rammenti quanto si è detto in relazione alla Fig. I.54 sul significato da assegnare alle frecce tratteggiate.)

Si tratta naturalmente di casi particolari (d'onde la specificazione in senso stretto) dei più generali:

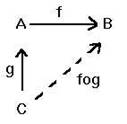
(Fig. I.A.12')
(Restrizioni di dominio "in senso lato")

 

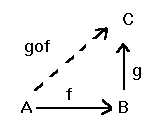
(Fig. I.A.13')
(Estensioni di codominio "in senso lato")

ai quali diamo ancora il nome di restrizioni di dominio ed estensioni di codominio (se si vuole specificare, in senso lato), anche se la funzione g che li determina non è più necessariamente un'inclusione, e nemmeno un monomorfismo (con la conseguenza che, qualche volta, l'insieme su cui si vuole restringere è "più grande" di quello di partenza, e quello su cui si vuole estendere è invece "più piccolo"; per la precisazione di tali nozioni anche nel caso di insiemi infiniti si veda il capitolo V).

Osserviamo esplicitamente che, fissato il morfismo g, la restrizione di dominio generale si riduce a un morfismo:

(I.A.14) res: H(A,B) ® H(C,B), res(f) = fog,

mentre l'estensione di codominio generale si riduce a un morfismo:

(I.A.14') ext: H(A,B) ® H(A,C), ext(f) = gof .

(Ritroveremo i due morfismi res ed ext nel capitolo IV, quando si parlerà del "bifuntore" Hom.)

Ciò visto, ci chiediamo adesso quando siano possibili invece estensioni di dominio e restrizioni di codominio, ovvero, ci proponiamo di discutere i seguenti diagrammi:

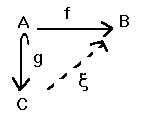
(Fig. I.A.15)
(Un'estensione di dominio in senso stretto)

 

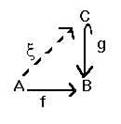
(Fig. I.A.16)
(Una restrizione di dominio in senso stretto)

Abbiamo adesso, in entrambi i casi, chiamato g l'inclusione canonica perché volevamo sottolineare le analogie con i rispettivi casi generali (in senso lato), illustrati dai seguenti diagrammi:

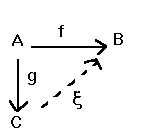
(Fig. I.A.17)
(Un'estensione di dominio in senso lato)

 

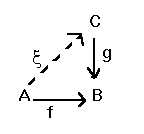
(Fig. I.A.18)
(Una restrizione di codominio in senso lato)

Come vedremo, la soluzione a questi problemi sarà a volte banale, a volte degna di qualche attenzione. Notiamo subito che, in ogni caso, essi si possono formulare mediante un'equazione "di primo grado", a coefficienti nel semigruppo parziale H() e nell'incognita x:

(I.A.19) xog = f (nel caso (I.A.17))

(I.A.20) gox = f (nel caso (I.A.18)).

Nelle dette equazioni l'incognita appare una volta a sinistra e una volta a destra, e si tratta di due alternative diverse l'una dall'altra, appunto perché il semigruppo che possiamo dire "ambiente" non è commutativo.

Cominciamo dalla (I.A.19) nel caso semplice (I.A.15). E' facile persuadersi che, se g è un'inclusione canonica, o più in generale un monomorfismo, l'equazione in parola ammette certamente soluzioni, anzi a priori più d'una, a meno che g non sia cancellabile a destra, nel qual caso la soluzione, se esistesse, sarebbe unica (ma si noti che, nelle attuali ipotesi, poiché la semiregolarità destra è la stessa cosa della suriettività, a norma di (I.8'), il caso si presenta solo quando g sia un isomorfismo, eventualmente un morfismo identità). In effetti, se A ¹ Æ, basta prendere una qualsiasi retrazione g' di g (si rammenti (I.31')) per essere sicuri che fg' Î H(C,B) è una soluzione. Infatti, dalla g'g = idA, si trae:
(fg')og = fo(g'g) = foidA = f (abbiamo appositamente alternato simbolo esplicito di composizione, e sua assenza, perché entrambe le notazioni sono assai comuni, e con esse è opportuno familiarizzare). Se invece A = Æ e B ¹ Æ, allora qualunque morfismo x Î H(C,B) funge da soluzione della (I.19) (quindi, anche quando g non è invertibile a sinistra, si rammenti ancora (I.31')), sicché si può concludere che l'equazione è quasi sempre risolubile quando g è un monomorfismo (con l'unica, al solito "sgradevole", eccezione, A = B = Æ e
C ¹ Æ; un'eccezione "simile" si trovava già del resto nel menzionato teorema (I.31')).

Allo stesso modo, è facile discutere la (I.A.20) non nel caso della Fig. I.A.16, ma quando g sia un epimorfismo. In tale eventualità infatti g ammette delle sezioni s Î H(B,C), gs = idB (si rammenti (I.32')), sicché sf Î H(A,C) risulta una soluzione dell'equazione in parola: go(sf) = (gs)of = idBof = f:

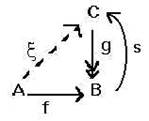
(Fig. I.A.21)
(Una particolare restrizione di codominio)

Si può concludere quindi che l'equazione è sempre risolubile quando g è un epimorfismo. La soluzione sarebbe pure unica qualora g fosse cancellabile a sinistra, ma ciò risulterebbe vero (in virtù di (I.9')), unicamente quando g fosse un monomorfismo, cioè, nelle attuali ipotesi, addirittura un isomorfismo.

Saliamo adesso di difficoltà, cominciando a indagare la (I.A.19) quando g (quello che conta in tutto questo discorso è ovviamente il "coefficiente" dell'equazione, ovvero il morfismo che risulta moltiplicato per l'incognita x) risulti invece un epimorfismo, come nella seguente figura, caso particolare naturalmente della Fig. I.A.17:

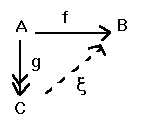
(Fig. I.A.22)
(Una particolare estensione di dominio)

In questo caso la nostra equazione potrebbe non avere alcuna soluzione. Non si faccia l'errore infatti di introdurre una sezione s di g, gs = idC, e di ritenere che
x = fs sia una soluzione: una volta che si sostituisse fs nella xog = f, si troverebbe (fs)g = f(sg) che non si sa quanto fa, perché s è generalmente soltanto inversa destra di g, e non sinistra. A prescindere da siffatte considerazioni di pura "algebra", basta ragionare un poco sulla situazione insiemistica. La g risulta certo invertibile a destra, ovvero è lecito in qualche modo tornare indietro da C ad A, per poi arrivare infine a B tramite f come si desidera, ma tale "ritorno" è altamente arbitrario, dipendendo dalla scelta di un certo rappresentante a Î A nella "fibra" g°(c) di un elemento c Î C. Come dire che, se tentiamo di porre x(c) = f(a), potremmo trovarci con qualche elemento a'x diverso da a che pure appartiene alla stessa fibra di a rispetto a g, sicché avremmo
x(g(a)) = x(c) = f(a), e va bene, ma anche x(g(a')) = x(c) = f(a'), la quale non va bene, perché violerebbe l'univocità della f, a meno che ... a meno che non risulti f(a) = f(a') tutte le volte che a e a' sono elementi di A appartenenti a uno stesso blocco della partizione associata a g. In questo caso infatti la definizione
x(c) = f(a) risulterebbe ben posta, ovvero, sarebbe indipendente dalla scelta del rappresentante a nel blocco g°(c), e questo morfismo x sarebbe palesemente una soluzione del nostro problema.

Ci troviamo quindi con una condizione sufficiente per la risolubilità della (I.A.19) nel caso particolare che g sia un epimorfismo. Basta che la partizione indotta da g su A risulti più fine della partizione indotta da f su A (si rammentino le considerazioni successive alla (I.18)), in simboli: Pf Ð Pg, in parole, che tutti i blocchi di f siano "più grandi" dei blocchi di g, unione cioè di essi, o, come anche si dice talvolta, che la partizione indotta da g su A sia "compatibile" con quella indotta da f su A. [Si noti bene che tale nozione di compatibilità richiede ovviamente per la sua formulazione la specificazione di un ben preciso ordine tra f e g. Solitamente si intende f già data per prima, e g è compatibile con f ses i blocchi di g sono tutti "all'interno" di blocchi di f, come è per esempio il caso del morfismo identità, g = idA, per il quale si può procedere banalmente alla richiesta estensione di dominio. Allo studente non sfuggirà la connessione tra le presenti argomentazioni, e quelle di cui al teorema (I.52).] E' evidente che la detta condizione sufficiente è anche necessaria per la risolubilità della nostra equazione, perché se esiste un morfismo x tale che f = xg, allora, assegnati due elementi a, a' Î A, tali che g(a) = g(a'), risulta necessariamente: f(a) = xg(a) = xg(a') = f(a'). Ci troviamo in definitiva in grado di formulare il seguente:

(I.A.23) Teorema. Nel caso che g sia un epimorfismo (ossia, C è isomorfo, "tramite g", a un insieme quoziente di A), è possibile risolvere un'equazione del tipo (I.A.19), ovvero procedere all'estensione di dominio corrispondente, se e soltanto se risulta Pf Ð Pg.

(La soluzione x risulta in questo caso addirittura univocamente determinata, una circostanza questa che non dovrebbe sorprendere, in quanto essendo g supposto ora un epimorfismo, esso risulta cancellabile a destra, in forza di (I.A.8).)

(Un caso particolare di (I.A.23) lo abbiamo già incontrato, in connessione al teorema di decomposizione (I.47): lì infatti si procedeva, data f : A ® B, all'estensione di dominio relativa alla proiezione canonica associata a f, cioè
p : A ® Pf; in effetti, in tale caso risultava Pp addirittura uguale a Pf.)

[La situazione illustrata nel teorema (I.A.23) diviene particolarmente importante quando al posto di C ci sia esattamente un insieme quoziente P di A, e g sia la proiezione canonica
p : A  P. Fissati adesso questi componenti del problema, ci si può chiedere quali siano i morfismi f, i "termini noti" della (I.A.19), per i quali l'equazione diventa risolubile, ovvero per i quali esiste una fattorizzazione sull'insieme quoziente, o anche che inducono una funzione sull'insieme quoziente (abbiamo notato infatti che tale funzione "indotta" è necessariamente unica, qualora esista). Aggiungiamo che, del resto, quello in esame è uno dei modi più consueti di introdurre funzioni su un insieme quoziente P di un insieme A: ci si limita cioè a definire le funzioni direttamente su A, e a verificare poi che esse soddisfano alla necessaria condizione di estensione di dominio (in questo caso speciale su un insieme "più piccolo" di quello di partenza!). Si tratta di quelle che si dicono le funzioni "invarianti" relative alla partizione assegnata, nel senso che la funzione assume identico valore su due elementi del dominio che appartengano al medesimo blocco della partizione, mentre una funzione invariante f si dice poi "caratterizzante" se essa è addirittura iniettiva sul quoziente, ovvero se due elementi di A hanno la stessa immagine tramite f ses appartengono allo stesso blocco di P. In questo caso la funzione f induce una rappresentazione fedele x di P nel codominio di f; continuiamo a chiamarlo B. Se f (e quindi x) sono pure suriettive, ecco che abbiamo una rappresentazione fedele di P sul codominio di f, ovvero un isomorfismo tra P e B, che può corrispondere talora a un modo di "descrivere" P, ovvero di "visualizzare" un ente altrimenti "astratto" quale un insieme quoziente con un altro ente, appunto B, di cui sia più facile formarsi un'immagine. Introducendo un esempio al quale siamo abituati dai tempi della scuola secondaria, se io dico che un certo triangolo - sottinteso del "piano ordinario" - è isoscele, o rettangolo, oppure no, etc., mi trovo di fronte a funzioni invarianti rispetto alla relazione di "uguaglianza" tra triangoli (i "blocchi" diventano adesso gli insiemi di tutti i triangoli "uguali" tra loro). Tali funzioni consentono l'utile doppio ragionamento, che se un dato triangolo T è isoscele, allora un triangolo T' uguale a T è pure isoscele, e che se viceversa un dato triangolo T è isoscele, mentre un altro T' non lo è, allora T e T' non possono essere uguali. Invece, se io fisso per esempio una retta r nel piano, che si decompone allora (in r e) in due semipiani "aperti" e disgiunti (di questa tripartizione, contando anche r, si è parlato prima del punto (I.18)), diciamoli 1 e 2, e dico che un triangolo è del tipo 1 se risulta tutto "interno" a 1, è del tipo 2 se risulta tutto interno a 2, mentre è del tipo 3 se è incidente alla retta r, non trovo ovviamente una funzione invariante rispetto all'uguaglianza dei triangoli. Avrei in ogni caso una funzione sull'insieme dei triangoli, certo, ma "inutile" ai fini dello studio della relazione di uguaglianza (la quale resta caratterizzata dai famosi "criteri di uguaglianza", siano uguali soltanto due lati e l'angolo compreso, etc.). Analoghi esempi, tratti sempre dalla geometria, comprenderebbero il caso dell'ordine di una curva algebrica, e così via. Si dovrebbe precisare in che modo si possa dar senso alle citate "espressioni linguistiche" mediante il linguaggio dei morfismi: basta prendere le funzioni che vanno dall'insieme di tutti i triangoli a quello delle due "parole" {isoscele, non-isoscele}, oppure {rettangolo, non-rettangolo}, etc.. E' chiaro che i blocchi associati a codeste funzioni sono assai "più grandi" di quelli corrispondenti alla nota "elementare" relazione di uguaglianza (che risulta quindi più fine delle bipartizioni isoscele, non-isoscele, etc., bipartizioni semplici ma non "banali"), e che il loro studio conduce "progressivamente" all'individuazione dei blocchi "più piccoli" e più interessanti.]

E nel "caso generale", se g è cioè una qualsiasi funzione? Al punto in cui siamo pervenuti, basta guardare il seguente diagramma per comprendere come bisogna procedere:

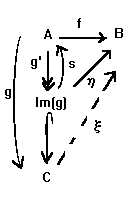
(Fig. I.A.24)

Si "spezza" ("fattorizza") g in un epimorfismo g' e in un'inclusione, quella che conta è naturalmente la parte relativa a g'. Se è possibile procedere all'estensione di dominio relativa a g', ovvero trovare una soluzione h dell'equazione hg' = f (nella Fig. (I.A.24) abbiamo anche indicato una sezione s di g' che serve per determinare la soluzione, h = fs), la soluzione x che andiamo cercando non è altro che una soluzione dell'estensione di dominio Im(g)  C, ovvero dell'equazione iox = h, e questa "seconda" equazione è per fortuna facile da risolvere, come abbiamo visto dianzi (ricordiamo, con l'unica eccezione
Im(g) = B = Æ, che è come dire A = B = Æ, e C ¹ Æ). In definitiva, poiché la partizione associata a g' è la stessa cosa della partizione associata a g, siamo condotti a concludere che il teorema (I.A.23) sussiste incondizionatamente, con l'unica detta eccezione:

(I.A.25) Teorema. Con l'esclusione del caso A = B = Æ, e C ¹ Æ, un'equazione del tipo (I.A.19) ammette soluzioni, ovvero si può procedere all'estensione di dominio corrispondente, se e soltanto se vale la relazione Pf Ð Pg. La soluzione risulta inoltre unica ses g è un epimorfismo.

(Per quanto riguarda la parte finale dell'enunciato, si osservi che, nel caso generale, si perde ovviamente l'unicità della soluzione nel "secondo tratto" dell'argomentazione.)

Passiamo adesso allo studio generale dell'equazione (I.A.20) (di cui ricordiamo che abbiamo già discusso il caso g epimorfismo), il quale risulta come vedremo alquanto più agevole dello studio della (I.A.19). Ancora una volta, per motivi "didattici", cominciamo a studiare il problema in un ulteriore caso particolare, quello cioè della Fig. I.A.16, o anche della Fig. I.A.18 nell'ipotesi però che il morfismo g sia un monomorfismo. E' chiaro adesso che, se esiste una soluzione x del tipo richiesto, allora, per ogni elemento a Î A, risulta f(a) = g(x(a)), ovvero, ogni elemento dell'immagine di f risulta in particolare un elemento dell'immagine di g: Im(f) Í Im(g) (si osservi che nelle ipotesi attuali non c'è più alcun problema relativo al "vuoto"). E' chiaro inoltre che codesta condizione necessaria per la risolubilità dell'equazione in esame è pure sufficiente nelle ipotesi attuali, perché se ogni elemento del tipo f(a) è anche un elemento del tipo g(c), per qualche elemento c Î C, allora un siffatto c è unico, in virtù dell'ipotesi di iniettività del morfismo g, sicché possiamo porre in ultima istanza x(a) = c, senza aver nulla a temere quanto a univocità della definizione di x. E' ovvio infine che il morfismo x appena definito è una soluzione del nostro problema. [Analogamente al caso precedente, che x risulti addirittura univocamente determinato tramite l'argomentazione riportata non dovrebbe sorprendere, in quanto essendo g supposto ora un monomorfismo, esso risulta cancellabile a sinistra, in forza di (I.A.9).]

Se g è addirittura un'inclusione, si dovrebbe riuscire a "visualizzare" immediatamente che l'unico caso in cui è possibile determinare la soluzione x è quello in cui f porti A esattamente "dentro" C: Im(f) Í C. Insomma, che si sia in presenza di uno schema del tipo seguente: A  Im(f)  C  A, dove il primo epimorfismo non è altro che f', la detta restrizione del morfismo f che sostituisce al codominio B l'immagine di f, e la richiesta soluzione x è il prodotto dei primi due morfismi dello schema. La seguente figura dovrebbe illustrare convenientemente la situazione appena descritta (f' designa come al solito l'epimorfismo restrizione di f alla propria immagine):

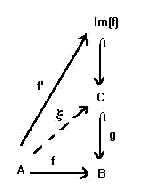
(Fig. I.A.26)

Senza raccogliere esplicitamente, come fatto in precedenza, il risultato particolare, passiamo adesso subito al caso generale. E' invero facile ormai concludere, semplicemente "guardando" il seguente diagramma:

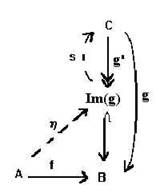
(Fig. I.A.27)

Si spezza cioè g come indicato nella figura, si effettua poi una "prima" estensione di codominio tramite il morfismo h quando si può, ovvero quando Im(f) Í Im(g), poi si effettua una "seconda" estensione di codominio andando a risolvere l'equazione xg' = h, che è "facile" perché g' è un epimorfismo (in questa seconda parte si perde eventualmente l'unicità della soluzione). In definitiva si ha allora il seguente:

(I.A.28) Teorema. Un'equazione del tipo (I.A.20) ammette soluzioni, ovvero si può procedere alla restrizione di codominio corrispondente, se e soltanto se vale la relazione Im(f) Í Im(g). La soluzione risulta inoltre unica ses g è un monomorfismo.

Dopo l'analisi di tanti diagrammi triangolari, chiudiamo con quella di alcuni diagrammi quadrati.

Dato il morfismo f : A ® B, nella seguente figura siamo di fronte a una doppia restrizione di dominio e di codominio (che potremmo chiamare un sollevamento di f, dalla coppia ordinata di insiemi A, B alla coppia ordinata di insiemi C,D):

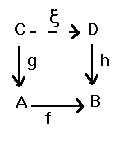
(Fig. I.A.29)

Nella successiva troviamo invece una doppia estensione di dominio e di codominio (che potremmo chiamare un abbassamento):

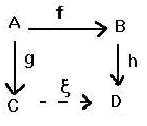
(Fig. I.A.30)

Dovrebbe essere ormai evidente che nel primo caso l'ostruzione (termine con cui si indica ciò che osta, ciò che si oppone a qualcosa) all'esistenza della soluzione viene dalla parte di destra del diagramma, cioè dalla restrizione di codominio della funzione fg tramite il morfismo h, mentre nel secondo l'ostruzione si trova a sinistra, cioè nell'estensione di dominio della funzione hf tramite il morfismo g, sed de hoc possiamo dire finalmente satis...

Costruzioni notevoli: prodotti e coprodotti fibrati

Veniamo adesso alle questioni menzionate nell'approfondimento posto dopo la dimostrazione del teorema (I.53), e alle costruzioni cui si era cominciato ad accennare con le Figg. da I.55 a I.58.

Iniziamo con le definizioni, e le "proprietà universali", di equalizzatore e coequalizzatore. [Come si sarà ormai compreso, questo prefisso "co" si utilizza in presenza di concetti "gemelli", o "duali", per esempio sezioni e cosezioni, retrazioni e coretrazioni; in topologia algebrica, che è stata una delle materie da cui è scaturita proprio la teoria delle categorie, si incontreranno omologia e coomologia, etc..] Siano date dunque due funzioni f, g Î H(A,B) come nella seguente figura:

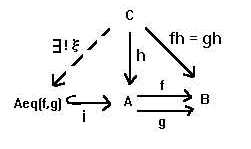
(Fig. I.A.31)
(L'equalizzatore di due funzioni)

Si chiama equalizzatore di f e g, e si indica con il simbolo Aeq(f,g) (dal latino aequalis), il sottoinsieme di A definito dalla:
Aeq(f,g) = {" x Î A ½ f(x) = g(x)}. Nel diagramma I.A.31 il morfismo i è l'inclusione canonica, h : C ® A è un qualsiasi morfismo tale che fh = gh. La "proprietà universale" dell'equalizzatore è che esiste un unico morfismo
x : C ® Aeq(f,g) tale che iox = h. La dimostrazione è facile, siamo nel caso di un'equazione del tipo I.A.20, la cui condizione necessaria e sufficiente di risolubilità è offerta dal teorema (I.A.28), ossia: Im(h) Í Im(i) = Aeq(f,g). E' chiaro che fh = gh corrisponde esattamente all'inclusione di Im(h) in Aeq(f,g), cvd. [Nel caso di un endomorfismo f : A ® A, si potrà sempre introdurre l'equalizzatore di f e idA, che è il sottoinsieme (che si indica anche con il simbolo Fix(f)) dei punti fissi di f, un concetto particolarmente importante per esempio nel caso di trasformazioni geometriche, o in spazi funzionali. La ricerca delle soluzione di un'equazione f(x) = 0, ci esprimiamo adesso in modo "vago", equivale alla determinazione dell'equalizzatore di f e della funzione "costante" k0, etc..]

Un po' più difficile è introdurre il coequalizzatore, Coaeq(f,g), delle due funzioni f e g, ma il "dualismo" con il caso precedente dovrebbe aiutare. Coaeq(f,g) è un insieme quoziente di B, che soddisfa la proprietà universale espressa nel seguente diagramma:

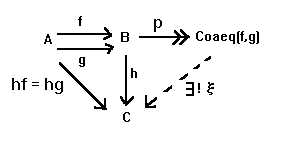
(Fig. I.A.32)
(Il coequalizzatore di due funzioni)

p è naturalmente la proiezione canonica sul quoziente, [Avremmo potuto sottolineare da tempo, lo facciamo solo adesso, che mentre esiste un apposito simbolo che distingue un generico monomorfismo da un'inclusione canonica, non ne abbiamo introdotto alcuno, e del resto non ne conosciamo di uso comune, atto a distinguere un generico epimorfismo da una proiezione canonica su un insieme quoziente. Eppure, questo è un concetto che possiamo considerare "duale" di quello di sottoinsieme di un dato insieme.] h è un qualsiasi morfismo da B a un qualsiasi insieme C tale che hf = hg. La proprietà universale del coequalizzatore è che esiste un unico morfismo
x : Coaeq(f,g) ® C tale che xop = h. Si tratta adesso di capire quale sia la partizione di B che soddisfa una tale condizione, collegata alla risolubilità di un'equazione del tipo (I.A.19), discussa nel teorema (I.A.25). La partizione individuata da p su B deve risultare più fine di tutte quelle individuate da funzioni h soddisfacenti alla hf = hg, e si comprende allora come i blocchi di Coaeq(f,g) debbano contenere soltanto gli elementi f(x) e g(x), al variare di x in A, quando si tratti di blocchi contenuti nell'unione delle due immagini Im(f) e Im(g), e un unico elemento z Î B quando questo non appartenga alla detta unione. Si tratta quindi di "monoblocchi" (o del tipo appena specificato, o quelli che corrispondono a elementi x nell'equalizzatore di f e g), mentre si hanno blocchi di cardinalità due a partire da elementi x tali che f(x) ¹ g(x). E' facile dimostrare che una tale partizione (si rammenti, un insieme quoziente di B) soddisfa alle condizioni sopra prescritte, si tratta di un altro istruttivo esercizio di pure "logica". [Nel teorema (I.A.25) si sottolineava l'esistenza di un'eccezione, corrispondente al solito caso "dell'insieme vuoto", però nelle attuali circostanza questo non presenta alcun problema.]

Introduciamo poi il concetto di unione disgiunta (o somma disgiunta) di due insiemi A e B, che viene indicata con il simbolo AB. Si tratta di immaginare un insieme X che "contenga" sia A che B, ma in modo tale che essi risultino disgiunti in X. Facciamo così conoscenza per la prima volta con un uso particolare in Algebra del termine "estensione" di qualcosa, per esempio come nel caso presente di un insieme. X non contiene nel senso proprio del termine né A né B (né potrebbe peraltro esistere un insieme con i requisiti desiderati qualora fosse AÇB ¹ Æ): ci si accontenta che X contenga un sottoinsieme, diciamolo A^, tale che esso sia isomorfo ad A (meglio naturalmente se isomorfo in qualche modo "naturale", come appunto adesso sarà il caso; si potrà parlare allora di una quasi-inclusione, un termine assai appropriato alla situazione, o di insiemi che sono immersi nella loro estensione tramite dei monomorfismi che allora vengono detti immersioni), e lo stesso per B. Onde costruire l'insieme X del tipo richiesto (o meglio, un insieme X; una volta però scelta una definizione di X, ci atterremo sempre strettamente a quella), basterà introdurre per esempio i due insiemi A´{1} e B´{2}, e considerarne l'unione insiemistica A´{1}ÈB´{2}. Vale a dire, si pone per definizione (con un certo ovvio "grado di arbitrarietà": anziché 1 e 2 avremmo potuto prendere due qualsiasi altri "oggetti" matematici distinti, per esempio 0 e 1, o Æ e {Æ}!):

(I.A.33) AB = A´{1}ÈB´{2},

essendo manifestamente A´{1} il ricercato sottoinsieme A^ di AB isomorfo in modo naturale ad A, e B´{2} l'analogo B^ (è chiaro che abbiamo agito in modo tale che risultasse A^ÇB^ = Æ).

(I.A.34) Nota. Si presti attenzione alla circostanza che si tratta di un'operazione che non è commutativa! Del resto la somma disgiunta di due insiemi A e B non è uguale ad AÈB neanche nel caso che A e B siano disgiunti; AB risulta solo canonicamente isomorfa a tale unione insiemistica (come si capisce subito).

Anche l'unione disgiunta di due insiemi soddisfa una sua "proprietà universale", [Siffatte proprietà universali hanno l'effetto, che sarà compreso in modo crescente via via che si procede nello studio, che un "oggetto" che le soddisfa resta univocamente determinato a meno di un ben determinato isomorfismo con un altro analogo, il che toglie in qualche modo un po' dell'arbitrarietà che può possedere una data costruzione come quella che stiamo attualmente esponendo, ma su ciò limitiamoci per il momento a questi brevi cenni.] che vediamo illustrata dal seguente diagramma:

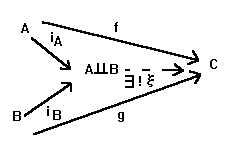
(Fig. I.A.35)
(La proprietà universale dell'unione disgiunta)

Qui iA e iB rappresentano rispettivamente le "immersioni" canoniche di A e B nella loro somma disgiunta, f e g sono due qualsiasi morfismi in un qualsiasi insieme C. Esiste uno e un solo morfismo x da AB in C tale che f = xoiA,
g = xoiB, il quale morfismo può indicarsi con il simbolo fg, e denominarsi la somma disgiunta delle due funzioni. Si tratta di un'affermazione del tutto evidente: la funzione x calcolata su un elemento del tipo (a,1) sarà semplicemente f(a), mentre x((b,2)) = g(b) (il simbolismo è scelto in maniera autoesplicativa). Lo studente noterà piuttosto il carattere assolutamente duale della costruzione rispetto alla Fig. I.82 (i versi delle "frecce" si scambiano, gli epimorfismi diventano monomorfismi, etc.), sicché l'operazione di somma disgiunta si può chiamare anche coprodotto.

Siamo in grado di passare adesso alla nozione di prodotto fibrato tra due insiemi A e C su una base B, in simboli (A´C)/B. Si tratta di una costruzione che generalizza come vedremo quella di prodotto cartesiano. Lì i due insiemi fattori erano "liberi", qui sono per così dire "vincolati" da due morfismi f e g, rispettivamente da A verso B, e da C verso B, su un terzo insieme B, come nel diagramma che segue:

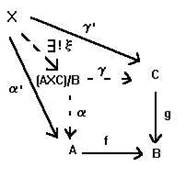
(Fig. I.A.36)
(La proprietà universale del prodotto fibrato)

Un prodotto fibrato (per essere più precisi, dell'intero "schema" comprendente i due morfismi f e g, non dei soli due insiemi!) è un insieme che soddisfa la proprietà universale indicata nella figura. Esso dovrà essere dotato di due opportuni morfismi canonici a e g, in A e in C ordinatamente, che rendono il diagramma (a, g, f, g) commutativo (il simbolo appena utilizzato non è "specifico", ma efficace), e sono universali rispetto a tale proprietà, nel senso che se X è un qualsiasi altro insieme dotato di due morfismi "analoghi" a', g', allora dovrà esistere un unico morfismo x da X verso il prodotto fibrato, tale che tutti i "sotto-diagrammi" che risultano all'interno del "diagramma ambiente" siano commutativi.

Allo studente non sfuggirà l'analogia con l'ordinario prodotto cartesiano, a cui in effetti il prodotto fibrato si "riconduce" (al solito, a meno di isomorfismi canonici), quando la base B sia ridotta a un singleton, e i morfismi f e g siano gli unici morfismi da A e C verso B (si rammenti la Fig. I.89, il singleton è un elemento finale di ).

Definito per il tramite di una proprietà universale come la precedente, un prodotto fibrato resterebbe univocamente determinato soltanto a meno di isomorfismi (canonici), sicché noi preferiremo al solito individuare una costruzione specifica che conduca a quello che potremo allora considerare il prodotto fibrato (A´C)/B che stiamo cercando. La figura seguente indica la non difficile procedura che porta alla sua esistenza, si tratterà poi di dimostrare che l'insieme così determinato soddisfa proprio i requisiti di cui alla figura I.A.36. Nel realizzare ciò bisognerà fare un po' di quello che abbiamo chiamato diagram chasing, e che lasciamo per "esercizio" al lettore più volenteroso.

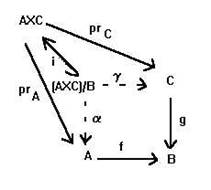
(Fig. I.A.37)
(La costruzione del prodotto fibrato)

Nella figura si è introdotto l'ordinario prodotto cartesiano A´C, con le relative proiezioni canoniche, che composte rispettivamente con f e con g danno due morfismi f' e g' da A´C verso la base B, i quali non soddisfano a priori alcuna particolare condizione. Se prendiamo però l'equalizzatore dei due morfismi, allora otteniamo un sottoinsieme di A´C (nella Fig. I.A.37 i indica la relativa inclusione canonica) tale che la prima proiezione composta con i individua un morfismo a tale che, se si indica con g il morfismo risultante dalla similare composizione della seconda proiezione con i, allora il prodotto fa è uguale al prodotto gg, e questo era esattamente uno dei requisiti che volevamo. Si comprende ormai come sia proprio tale sottoinsieme quello che chiameremo il prodotto fibrato (A´C)/B (ossia, l'insieme delle coppie ordinate (a,c), " a Î A, " c Î C, tali che f(a) = g(c)), perché soddisfa, insieme ai detti morfismi, la proprietà universale che avevamo proposto di "risolvere" (la funzione x non è altro che l'ordinario prodotto cartesiano a'´g', "modulo" una restrizione di codominio che risulta attualmente possibile in forza delle ipotesi).

In maniera del tutto simile (come abbiamo detto, duale) si introduce il concetto di coprodotto fibrato (o di somma disgiunta fibrata) di due insiemi B e C su una certa base A, che indicheremo con il simbolo (BC)/A ("giochiamo" apposta con le "variabili mute" per non "impigrire" la memoria con simboli che rivestono sempre lo stesso ruolo), e la cui proprietà universale viene illustrata dal seguente diagramma:

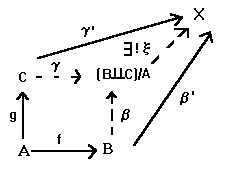
(Fig. I.A.38)
(La proprietà universale del coprodotto fibrato)

Abbiamo indicato adesso con A la "base", e con f e g due morfismi dalla base verso i due insiemi, peraltro arbitrari come f e g, B e C. Il coprodotto fibrato deve possedere una coppia di morfismi b, g come in figura, i quali siano "universali" rispetto all'identità bf = gg.

La costruzione del coprodotto fibrato è del tutto analoga a quella del prodotto fibrato (e per essa si possono ripetere tutte le precedenti osservazioni). Si tratta di prendere adesso la somma disgiunta BC, con le due immersioni canoniche iB e iC, indi considerare il coequalizzatore di iBf e di iCg. Detta p la relativa proiezione canonica (che nella seguente figura non è denominata), è chiaro che iBp e di iCp sono due morfismi b, g che soddisfano l'"equazione" bf = gg. Dimostrare che essi sono soluzioni universali di tale equazione è questione di un altro po' di sfoggio di diagram chasing, si tratta di mète non proprio difficili alle quali pervenire da soli (la funzione x non è altro adesso che l'ordinario coprodotto cartesiano b'g', "modulo" un'estensione di dominio che risulta attualmente possibile in forza delle ipotesi).

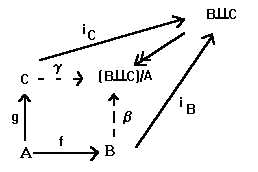
(Fig. I.A.39)
(La costruzione del coprodotto fibrato)

Osserviamo piuttosto, per concludere, che il coprodotto fibrato si riduce manifestamente all'unione disgiunta ordinaria (coprodotto) quando la base A sia il vuoto (si rammenti la Fig. I.88, il vuoto è l'unico elemento iniziale di ), e che in questa sezione si sono indagate tutte proprietà (e costruzioni) che risulta piuttosto agevole analizzare nella categoria degli insiemi, in cui ci sono "tanti" morfismi a disposizione. L'identica situazione formale si fa invece maggiormente complessa, e in modo proporzionale anche più interessante, quando lo studio di essa si riproponga in altre diverse categorie, dove alla ricchezza delle strutture fa da contraltare la riduzione del "numero" dei morfismi, e non sarà allora sufficiente trovare per esempio una funzione che soddisfi certe desiderate proprietà. La vorremo infatti soddisfacente anche quelle particolari condizioni che "caratterizzano" i morfismi della categoria, quali la continuità se si tratta di spazi topologici, o certe proprietà di tipo algebrico nel caso si tratti di strutture algebriche, etc., c'è di che non annoiarsi... [Si tenga però presente che è un segno di "degenerazione" che l'impresa matematica sia intesa unicamente sotto il profilo "ludico-enigmistico" o "estetizzante", cioè come sforzo rivolto alla risoluzione di qualcuno degli infiniti problemi che si possono confezionare con i suoi "oggetti". Allo stesso modo non si dovrebbe essere condotti a formulare o condividere "giudizi di valore" secondo i quali un matematico va considerato "bravo" quando è riuscito a risolvere questioni difficili che altri non erano riusciti a risolvere prima di lui (si verifica infatti il fenomeno dell'emulazione inconsapevole), senza che si sappia allo stesso tempo rispondere a domande di "significato" in ordine a ciò che è stato realizzato. In questo senso le "applicazioni" della matematica (quando non siano, come purtroppo talora accade, "artificiose" allo scopo di costruirsi una reputazione adeguata verso l'esterno), non sono soggette a tale tipo di critica, ma si deve precisare che le ricadute di una "ricerca" matematica possono anche essere di tipo non strettamente "pratico" (per esempio volte all'utilizzo immediato da parte di banche o imprenditori, come oggi va di moda), essendo legittimo valutarle, da parte di chi è in grado di farlo, in funzione del loro contributo a una crescente comprensione del corpus della matematica stessa, vale a dire, ad maiorem Dei (sive Hominis) gloriam.]