Pi greco

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Pi greco

I numeri e e sono numeri irrazionali trascendenti:
irrazionale perché non è esprimibile come rapporto fra due numeri interi
trascendente perché l’equazione che lo definisce trascende le normali operazioni di calcolo.
Pi-greco -
3,14 .....così ce lo hanno insegnato a scuola , quel numero che serve ad esempio a calcolare l'area di un cerchio.
Ma quel numero come si calcola e perché?
Fino a quante cifre decimali di pi greco la mente umana conosce?
Che cosa è pi?
Pi greco o pi per gli amici è definito come il rapporto fra una qualsiasi circonferenza C e il il suo diametro d=2r.
= C/d = C/2r
Pi è un numero irrazionale e trascendente. Ecco le sue prime 999 cifre decimali.
Le prime 999 cifre di pi greco.
Meno di un granello di sabbia nell'Universo.
3.141592653589793238462643383279502884197169399375
10582097494459230781640628620899862803482534211706
79821480865132823066470938446095505822317253594081
28481117450284102701938521105559644622948954930381
96442881097566593344612847564823378678316527120190
91456485669234603486104543266482133936072602491412
73724587006606315588174881520920962829254091715364
36789259036001133053054882046652138414695194151160
94330572703657595919530921861173819326117931051185
48074462379962749567351885752724891227938183011949
12983367336244065664308602139494639522473719070217
98609437027705392171762931767523846748184676694051
32000568127145263560827785771342757789609173637178
72146844090122495343014654958537105079227968925892
35420199561121290219608640344181598136297747713099
60518707211349999998372978049951059731732816096318
59502445945534690830264252230825334468503526193118
81710100031378387528865875332083814206171776691473
03598253490428755468731159562863882353787593751957
78185778053217122680661300192787661119590921642019...

La costante matematica π ( si scrive "pi" dove le lettere greche non sono disponibili) è utilizzata moltissimo in matematica e fisica. Nella geometria piana, π viene definito come il rapporto tra la circonferenza e il diametro di un cerchio, o anche come l'area di un cerchio di raggio 1. Molti libri moderni di analisi matematica definiscono il π usando le funzioni trigonometriche, per esempio come il più piccolo numero per cui sin(x)=0 oppure il più piccolo numero che moltiplicato per 2 annulla cos(x). Tutte le definizioni sono equivalenti.
π è conosciuto anche come la costante di Archimede (da non confondere con i numeri di Archimede), la costante di Ludolph o numero di Ludolph. Contrariamente ad una idea comune, π non è una costante fisica o della natura, quanto piuttosto una costante matematica definita in modo indipendente dalle misure di carattere fisico.
Proprietà
π è un numero irrazionale, non può cioè essere scritto come quoziente di due interi. Questo è stato provato nel 1761 da Johann Heinrich Lambert. Inoltre, è un numero trascendente, come è stato provato da Ferdinand von Lindemann nel 1882. Questo significa che non ci sono polinomi con coefficienti interi o razionali di cui π è radice. Di conseguenza, è impossibile esprimere π usando un numero finito di interi, di frazioni e delle loro radici.
Questo risultato stabilisce l'impossibilità della quadratura del cerchio, cioè la costruzione, con solo riga e compasso, di un quadrato della stessa area di un dato cerchio.
[modifica]
Formule che riguardano π
Geometria:
La circonferenza di un cerchio o di una sfera di raggio r: C = 2 π r
L'area di un cerchio di raggio r: A = π r2
L'area di un'ellisse di semiassi a e b: A = π ab
Il volume di una sfera di raggio r: V = (4/3) π r3
La superficie di una sfera di raggio r: A = 4 π r2
Il volume di un cilindro di altezza h e raggio r: V = (π r2 ) h
L'area della superficie di un cilindro di altezza h e raggio r: A = ([π r2] 2 ) + ([2 π r] h )
Angoli: 180 gradi equivalgono a π radianti

Analisi:
$\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}$
Formula di Leibniz.
$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}$
Prodotto di Wallis.
$\zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$
Il problema di Basel, risolto da Eulero. Vedi anche la funzione zeta di Riemann.
$\zeta(4)= \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}$
$\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}$
$\Gamma\left({1 \over 2}\right)=\sqrt{\pi}$
$n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$
Approssimazione di Stirling.
$\sum_{k=0}^{n} \phi (k) \sim 3 n^2 / \pi^2$
$e^{\pi i} + 1 = 0\;$
L'identità di Eulero, definita da Richard Feynman "la più notevole formula della matematica".
π ha delle bellissime rappresentazioni come frazioni continue:
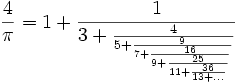
$\frac{4}{\pi} = 1 + \frac{1}{3 + \frac{4}{5 + \frac{9}{7 + \frac{16}{9 + \frac{25}{11 + \frac{36}{13 + ...}}}}}}$
(È possibile trovare altre 12 rappresentazioni a [1] (http://functions.wolfram.com/Constants/Pi/10/) )
Teoria dei numeri:
La probabilità che due interi scelti a caso siano primi fra loro è di 6/π2
Il numero medio di modi in cui è possibile scrivere un intero positivo come somma di due quadrati perfetti è π/4.
Dynamical Systems / Ergodic theory:
$\lim_{n \to \infty} \frac{1}{n} \sum_{i = 1}^{n} \sqrt{x_i} = \frac{2}{\pi}$
for almost every x0 in [0, 1] where the xi are iterates of the Logistic map for r=4.
Fisica:
$\Delta x \Delta p \ge \frac{h}{4\pi}$
Principio di indeterminazione di Heisenberg.
$R_{ik} - {g_{ik} R \over 2} + \Lambda g_{ik} = {8 \pi G \over c^4} T_{ik}$
Equazione di campo di Einstein della relatività generale.
$F = \frac{\left|q_1q_2\right|}{4 \pi \epsilon_0 r^2}$
Forza di Coulomb.
Probabilità e statistica:
$f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{-{(x-\mu )^2 \over 2\sigma^2}}$
La funzione della densità probabile nella distribuzione normale.
$\pi = \frac{2ln}{th}$
Buffon's needle
Storia
Il simbolo "π" per la costante di Archimede è stato introdotto nel 1706 da William Jones quando pubblicò A New Introduction to Mathematics, benché lo stesso simbolo fosse stato utilizzato in precedenza per indicare la circonferenza del cerchio. La notazione diventò standard dopo che la utilizzò Eulero. In entrambi i casi π è la prima lettera di περιμετροσ (perimetros), che significa 'misura attorno' in greco.
Ecco una breve cronologia di π:

20° secolo AC: i Babilonesi usavano 25/8 per π
20° secolo AC: gli Egizi usano π = (16/9)2
12° secolo AC: i Cinesi usano 3 per π
434 AC: Anassagora tenta la quadratura del cerchio con riga e compasso
3° secolo AC: Archimede scopre che 223/71 < π < 22/7, e trova inoltre l'approssimazione π = 211875/67441.
20 AC: Vitruvio usa 25/8.
2° secolo: Tolomeo usa π = 377/120.
3° secolo: Chang Hong usa π = √10, Wang Fau usa π = 142/45, e Liu Hui usa π = 471/150.
5° secolo: Zu Chongzhi scopre che 3.1415926 < π < 3.1415927.
6° secolo: Aryabhatta e Brahmagupta, in India, usano rispettivamente il valore 62832/20000 e √ 10.
9° secolo: Al Khwarizmi usa 3.1416.
1220: Fibonacci usa il valore 3.141818.
1430: Al Kashi calcola le prime 14 cifre di π.
1573: Valenthus Otho calcola le prime 6 cifre di π.
1593: François Vieta calcola 9 cifre di π e Dutch Adriaen van Roomen 15 cifre.
1596: Ludolph van Ceulen calcola 35 cifre di π.
1665: Isaac Newton, 16 cifre.
1699: Sharp, 71 cifre.
1700: Seki Kowa, 10 cifre.
1730: Kamata, 25 cifre.
1706: Machin, 100 cifre.
1719: De Lagny calcola 127 cifre, di cui 112 sono corrette.
1723: Takebe, 41 cifre.
1734: Adottato da Eulero, l'uso del simbolo π si diffonde.
1739: Matsunaga, 50 cifre.
1761: Johann Heinrich Lambert prova che π è un numero irrazionale.
1775: Euler ipotizza che π possa essere transcendente.
1794: von Vega, 140 cifre, di cui 136 sono corrette.
1794: Adrien-Marie Legendre dimostra che π2 (e quindi π) è irrazionale, e considera la possibilità che π sia trascendente.
1824: Rutherford calcola 208 cifre, di cui 152 sono corrette.
1844: Strassnitzky calcola fino a 200 cifre.
1847: Thomas Clausen, 248 cifre.
1853: Lehmann, 261 cifre.
1853: Rutherford, 440 cifre.
1855: Richter, 500 cifre.
1874: Shanks, 707 cifre, di cui 527 sono corrette.
1882: Lindemann dimostra che π è trascendente.

Approssimazioni numeriche di π
A causa della sua natura trascendente, non ci sono semplici espressioni finiti che rappresentano π. Di conseguenza i calcoli numerici devono usare approssimazioni del numero. In molti casi, 3,14 o 22/7 è sufficente, ma molti ingegneri spesso usano 3,1416 (cinque cifre significative) o 3,14159 (6 cifre significative).
Un scriba egizio di nome Ahmes è l'origine del più antico testo conosciuto contenente un'approssimazione di π. Il papiro di Rhind è datato al 17° secolo AC e descrive il valore come 256/81 oppure 3,160.
Il matematico cinese Liu Hui calcolò π come 3,141014 (scorretto dalla quarta cifra decimale) nel 263 D.C. e suggerì 3,14 come buona approssimazione.
Il matematico ed astronomo cinese Zu Chongzhi calcolò nel 5° secolo π come compreso fra 3,1415926 e 3,1415927 e diede due approssimazioni di π: 355/113 e 22/7.
Il matematico ed astronomo iraniano Ghyath ad-din Jamshid Kashani, 1350-1439, calcolò le prime 9 cifre in base 60 di π, che sono equivalenti nella base decimale alle 16 cifre:
2 π = 6,2831853071795865
Il matematico tedesco Ludolph van Ceulen (1600 circa) calcolò i primi 35 decimali. Era così fiero del suo risultato che lo fece scrivere sulla sua lapide.
Il matematico sloveno Jurij Vega nel 1789 calcolò le prime 140 cifre decimali di π, di cui le prime 137 erano corrette, e mantenne il record mondiale per 52 anni, fino al 1841, quando William Rutherford calcolò 208 cifre decimale di cui le prime 152 erano corrette. Vega migliorò la formula di John Machin nel 1706.
Nessuna delle formule sopraelencate può fornire un'efficiente metodo per l'approssimazione di π. Per calcoli veloci, si può usare una formula come quella di Machin:
$\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}$
Insieme con l'espansione delle serie di Taylor per la funzione arctan(x). Questa formula si può verificare facilmente usando le coordinate polari dei numeri complessi, partendo da:
$(5+i)^4\cdot(-239+i)=-114244-114244i.$
Formule di questo genere sono note come formule di tipo Machin.
Espansioni decimali molto lunghe di π sono calcolate tipicamente con l'algoritmo Gauss-Legedre e l'algoritmo Borwein; in passato era usato anche l'algoritmo Salamin-Brent, inventato nel 1976
L'elenco del primo milione di cifre di π e di 1/π si può trovare sul Progetto Gutenberg (vedi il collegamento esterno a fondopagina). Il record attuale (Dicembre 2002) è di 1.241.100.000.000 di cifre, calcolate nel settembre 2002 su un supercomputer Hitachi a 64 nodi con un terabyte di memoria principale, in grado di compiere 2 bilioni di operazioni per secondo, quasi il doppio del computer usato per il precedente record (206 miliardi di cifre). Sono state usate le seguenti formule di tipo Machin:
$\frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443}$
K. Takano (1982).
$\frac{\pi}{4} = 44 \arctan\frac{1}{57} + 7 \arctan\frac{1}{239} - 12 \arctan\frac{1}{682} + 24 \arctan\frac{1}{12943}$
F. C. W. Störmer (1896).
Queste approssimazioni sono così complesse da non essere utili per nessuno scopo pratico, se non per provare nuovi supercomputer.
Nel 1996 David H. Bailey, insieme a Peter Borwein e Simon Plouffe, scoprì una nuova formula per calcolare π come serie infinita:
$\pi = \sum_{k = 0}^{\infty} \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right)$
Questa formula permette di calcolare facilmente la k-esima cifra binaria o esadecimale di π senza dover calcolare tutte le cifre precedenti. Il sito web di Bailey (http://www.nersc.gov/~dhbailey/) ne contiene l'implementazione in vari linguaggi di programmazione.
Alcune altre formule usate per calcolare stime di π sono:
$\frac{\pi}{2}= \sum_{k=0}^\infty\frac{k!}{(2k+1)!!}= 1+\frac{1}{3}\left(1+\frac{2}{5}\left(1+\frac{3}{7}\left(1+\frac{4}{9}(1+...)\right)\right)\right)$
Newton.
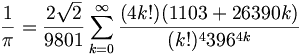
$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k!)(1103+26390k)}{(k!)^4 396^{4k}}$
Ramanujan.
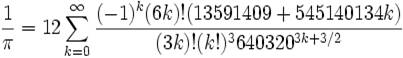
$\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}$
David Chudnovsky e Gregory Chudnovsky.
${\pi} = 20 \arctan\frac{1}{7} - 8 \arctan\frac{3}{79}$
Eulero.
Questioni aperte
La più pressante questione aperta su π riguarda il fatto che sia o meno normale, cioè se la frequenza con cui è presente ogni sequenza di cifre sia la stessa che ci si aspetterebbe se le cifre fossero completamente casuali. Questo deve essere vero in ogni base, non solo in base 10. Non sappiamo molto su questo.
Bailey e Crandall dimostrarono nel 2000 che l'esistenza della sovramenzionata formula Bailey-Borwein-Plouffe e formule simili implica la normalità in base 2 di π. Vedi il sovramenzionato sito web di Bailey per ulteriori informazioni.
La natura di π
Nelle geometrie non-euclidee la somma degli angoli interni di un triangolo può essere maggiore o minore di π e il rapporto fra una circonferenza ed il suo diamentro può non essere π. Questo non cambia la definizione di π, ma influisce su qualsiasi formula in cui appare π. Quindi, in particolare, π non è legato alla forma dell'universo; è una costante matematica, non fisica.
Cultura legata al Pi greco
C'è un intero campo di studi divertenti ma seri che riguardano l'uso di tecniche di memorizzazione per ricordare le cifre di π.
Collegamenti esterni

Wikisource - Pi fino alla cifra 1.000 (http://sources.wikipedia.org/wiki/Pi_to_1%2C000_places) | alla cifra 10.000 (http://sources.wikipedia.org/wiki/Pi_to_10%2C000_places) | alla cifra 100.000 (http://sources.wikipedia.org/wiki/Pi_to_100%2C000_places)
Un testo del Progetto Gutenberg contenente un milione di cifre di pi (http://www.gutenberg.net/etext/50)
Statistiche sui primi 1,2 bilioni di cifre di pi (http://www.super-computing.org/pi-decimal_current.html)
PiHex Project (http://www.cecm.sfu.ca/projects/pihex/index.html)
J J O'Connor e E F Robertson: A history of Pi. Mac Tutor project (http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Pi_through_the_ages.html)
Andreas P. Hatzipolakis: PiPhilology. Un sito con centinaia di modi per ricordare π (http://www.cilea.it/~bottoni/www-cilea/F90/piph.htm)
Molte formule per π, dal sito della Wolfram Mathematics (http://mathworld.wolfram.com/PiFormulas.html)
Alla ricerca del valore di Pi (http://mathforum.org/isaac/problems/pi1.html)
PlanetMath: Pi (http://planetmath.org/encyclopedia/Pi.html)
Il pi-hacks Yahoo! Group (http://groups.yahoo.com/group/pi-hacks)
Una pagina con circa 220 milioni di cifre del pi greco (http://3.14.maxg.org/)
http://3.141592653589793238462643383279502884197169399375105820974944592.com
Una raccolta di formule di tipo Machin per i calcolo del pi greco (http://machination.mysite.freeserve.com/)
Una prova del fatto che Pi è irrazionale (http://www.lrz-muenchen.de/~hr/numb/pi-irr.html)

Breve storia di un numero famoso: p
Dai babilonesi ... ai giorni nostri.
Vittorio De Petris
Scuola Media "D.Alighieri" - L'Aquila

Liberamente tratto da «Storia del Pensiero Matematico» di Morris Kline - Giulio Einaudi Editore 1991

Il nome di babilonesi viene dato ad una serie di popolazioni che, in tempi successivi, occuparono la Mesopotamia, una regione del Medio Oriente situata tra il Tigri e l'Eufrate. Tra di esse ricordiamo le popolazioni dei Sumeri, che per primi occuparono tale regione a partire dal 4000 a.C., seguiti dagli Akkadi (2200 a.C.), dagli Assiri (800 a.C.), dai Caldei (700 a.C.), dai Persiani (540 a.C.), fino alla conquista della Mesopotamia da parte di Alessandro Magno nel 330 a.C. Il massimo periodo di fioritura della cultura babilonese si ebbe tra il 2200 a.C. e il 1700 a.C.
In Mesopotamia il ruolo della geometria era insignificante e quasi sempre legato ad applicazioni pratiche. Essi conoscevano certamente il teorema di Pitagora e la similitudine dei triangoli. Per ottenere l'area del cerchio usavano la formula A=c2/12,dove c indica la circonferenza. Ciò equivale ad usare per p il valore 3.
E' da 3 (come nel film di Troisi) che comincia dunque la nostra storia.
Per calcolare la lunghezza della circonferenza inscritta nell'esagono regolare, i babilonesi usavano un rapporto che implicava per p il valore di 3+1/8, che equivale a 3,125.
Il valore assegnato a p dai babilonesi era approssimato per difetto. Gli antichi egizi assegnavano invece a p un valore approssimato per eccesso. Essi calcolavano l'area del cerchio mediante la formula A=(8/9 d)2,dove d è il diametro. In questo caso p assume il valore 256/81 (circa 3,1605).

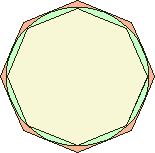Occorre arrivare al grande Archimede di Siracusa (287-212 a.C.), per avere i primi due decimali esatti di p. Egli cerca di calcolare la lunghezza della circonferenza per mezzo del perimetro dei poligoni inscritti e circoscritti. La circonferenza ha infatti una lunghezza compresa tra il perimetro di un poligono inscritto e quello di un poligono circoscritto ad essa.
Le misure di tali perimetri si avvicinano sempre più tra loro con l'aumentare del numero dei loro lati, permettendo di restringere sempre più l'intervallo entro il quale dev'essere compresa la misura della circonferenza che si desidera trovare.

Per tale via, egli riesce quindi a stabilire due valori tra cui p è compreso: (3+10/71) <p < (3+1/7). Il primo dei due valori vale 3,1408... e il secondo vale 3,1428...
Sono occorsi quasi due millenni per passare da una a tre cifre esatte del nostro numero.
Non basterà invece il tempo passato e futuro dell'umanità per trovare tutte le altre cifre. E' stato dimostrato infatti da Lambert nel 1761 che p è un numero irrazionale. Perciò le sue cifre decimali sono illimitate e non periodiche e nessuno potrà mai scriverle tutte. Successivamente, nel 1882, Lindemann dimostrò che p è un numero trascendente (significa che esso non può essere ottenuto da un'equazione algebrica a coefficienti razionali), ponendolo in una particolare categoria di numeri irrazionali, che si distinguono rispetto a quelli cosiddetti algebrici .
Pur non potendo quindi scrvere tutte le cifre di p, alcuni grandi matematici hanno tuttavia affrontato il problema di scoprire un procedimento che permettesse di trovare quante cifre decimali si desiderano.
Riprendiamo quindi il nostro racconto per descriverne le tappe più significative.
I romani, si sa, non dedicavano molti sforzi allo studio delle scienze (che non fossero quelle giuridiche o militari). Essi si limitarono alla conoscenza, senza ulteriori approfondimenti, delle opere dei greci. Gran parte della geometria di Archimede, per via della sua complessità, finì per essere dimenticata.
Gli uomini del medio evo dovevano risolvere problemi di stretta sopravvivenza (del corpo e dell'anima) e non potevano certo dedicarsi agli studi.
Dobbiamo perciò arrivare al Rinascimento, per assistere ad uno spettacolare rifiorire della scienza. In tale periodo, tra i matematici, si sviluppò un'ampia ricerca sui numeri irrazionali.
François Viète (1540-1603), riprendendo il metodo di Archimede ed usando le radici quadrate, calcolò il valore di p considerando poligoni regolari di 4, 8, 16,... lati inscritti in un cerchio di raggio unitario. Per tale via egli trovò che il valore di p è dato da:

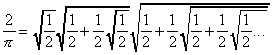
Il reciproco del valore ottenuto, moltiplicato per 2, fornisce un valore sempre più approssimato di p, quanto maggiore è il numero di termini. I primi quattro termini forniscono il valore approssimato 3,140331 con le prime due cifre decimali esatte. Con sei termini si ha: 3,141513, le cui prime quattro cifre decimali sono esatte. Occorrono dieci termini per avere sei cifre decimali esatte: 3,141592...
L'inglese John Wallis, nella sua Arithmetica infinitorum (1655), usò una frazione, i cui termini sono costituiti da una serie ininterrotta di moltiplicazioni. Dal numero di fattori usati dipende l'approssimazione di p:
p/4 = (3.3.5.5.7.7...)/(2.4.4.6.6.8...)

Wallis usava numeri razionali per calcolare p, contrariamente a Viète che usava le radici quadrate. Tuttavia la formula di Wallis richiede almeno 1000 termini per avere le prime due cifre decimali esatte di p.
Il grande Gottfried Wilhelm von Leibniz ottenne nel 1674 il famoso risultato:

Siamo dunque arrivati a definire p come il quadruplo della somma a segni alternati dei reciproci nella successione dei numeri dispari. Peccato che occorrano ben 764 termini per calcolare p anche solo con la precisione ottenuta da Archimede.
A questo punto va detto che il nostro p non ha ancora assunto il suo attuale nome.
Fu il matematico inglese William Jones che, nel 1706 usò il simbolo p, in onore di Pitagora (l'iniziale di Pitagora nell'alfabeto greco è appunto P, ma, trattandosi di un numero, si preferisce usare la minuscola ). Tuttavia, ancora nel 1739 lo svizzero Leonhard Euler (1707-83), da noi italianizzato in Eulero, usava il simbolo p.
Fu proprio Euler nel 1743 a fornire una ennesima formula per il calcolo di p:

La formula di Euler è più efficace di quella di Leibniz, per il fatto di usare solo termini positivi. Essa richiede tuttavia un numero di termini ancora piuttosto alto per ottenere le prime due cifre decimali esatte di p. Per avere 3,14 occorrono almeno 600 termini, contro i 764 richiesti dalla formula di Leibniz.
Non bisogna tuttavia pensare che ciò costituisca un problema per un matematico. Per la sua mentalità, è sufficiente che il metodo proposto, facendo uso di una formula possibilmente elegante, garantisca di trovare quante cifre decimali si vogliano di p. Che poi occorrano milioni di termini per avvicinarsi lentamente ai risultati desiderati è un fatto del tutto secondario e marginale!
Del resto il problema dei calcoli, al giorno d'oggi, è effettivamente diventato secondario. Disponiamo ormai di super calcolatori che riescono a fare milioni di operazioni al secondo. E' perciò possibile ottenere migliaia di cifre esatte di p, anche se poi resta da chiedersi a cosa potranno servire.

Fonte: http://www.alessandrobonini.it/download/matematica/Pi.doc

Sito web da visitare: http://www.alessandrobonini.it/

Autore del testo: non indicato nel documento di origine

Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.

Pi greco

"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco

www.riassuntini.com dove ritrovare l'informazione quando questa serve